A regressziós együtthatók és a korreláció fontosságának ellenőrzése a f-teszt segítségével

Std. est hibája. = 79,243276

A döntés a "Microstat" PC-program szerint készült. Íme a táblázatok a kinyomtatott lapon: fül. A 8.7. Ábra megadja az átlagértékeket és az összes jellemző négyzetes átlagát. Táblázat. A 8.8. Tartalmazza a regressziós együtthatókat és azok valószínűségi becslését:

az első grafikon "var" - változók, azaz faktorok; a második oszlop "regressziós együttható" - a feltételesen tiszta regresszió bj; a harmadik oszlop "std. errror "- a regressziós együtthatók becsléseinek átlagos hibái; a negyedik gráf - a Student's t-teszt értékei 12 fokos szabadságváltozással; az ötödik gráf "prob" - a nullhipotézis valószínűsége a regressziós együtthatókra vonatkozóan;

y = 2,26x1 - 4,31x2 + 0,166x3 - 240.

Ez azt jelenti, hogy a bruttó jövedelem értéke 1 hektár mezőgazdasági területre átlagosan 2,26 rubel. a munkaerőköltségek emelkedésével 1 óra / ha; csökkent átlagosan 4,31 rubel. a termőföldek részarányának növekedése 1% -kal nőtt és 0,166 rubelrel emelkedett. a tehenre jutó tejhozam 1 kg-os növekedésével. A szabadidő negatív értéke teljesen természetes, és - amint azt már a 8.2. Bekezdésben is megjegyeztük - a tényleges mutató - a bruttó jövedelem nulláig változik, mielőtt a termelésben lehetetlenné vált tényezők nulladik értékeit elérnék.

A negatív érték együttható x ^ - jel baj jelentős gazdaság vizsgált gazdaságokban, ahol a növénytermesztés veszteséges, és nyereséges csak állattenyésztéssel. Ha ésszerű mezőgazdasági gyakorlatok és normál áron (egyensúly, vagy ahhoz közel) a termék minden iparágban, a jövedelem nem csökkenhet, és növeli a legtermékenyebb mezőgazdasági területek részaránya - szántó.

A táblázat utolsó előtti két sorának adatai alapján. 8.7 és táblázat. 8.8 kiszámítja a (8.34) és (8.35) képletek szerinti p-együtthatókat és rugalmassági együtthatókat [4]

Egy másik változat a jövedelmi szint és annak esetleges módosítását a dinamikája az befolyásolja leginkább a tényező x3 - termelés a tehenek és a leggyengébb - x2 - a szántóföld aránya. A P2 / értékeket később kell használni (8.9. Táblázat);

8.9. Táblázat A tényezők jövedelmi szintre gyakorolt ​​összehasonlító hatása

Így azt találtuk, hogy a xj tényező együtthatója a tényező rugalmassági együtthatójára vonatkozik, mint a faktor variációs együtthatója a kapott tulajdonság variációs koefficiensére. Mivel, amint az a táblázat utolsó sorjából látható. 8.7., Az összes tényező variációs együtthatója kisebb, mint a tényleges tényező variációs együtthatója; minden? koefficiens kisebb, mint a rugalmassági együtthatók.

Tekintsük a paritás és a feltételesen tiszta regressziós tényező közötti paritást a tényező példáján. Az y páros lineáris kapcsolási egyenlet x-vel a következő alakú:

y = 3,886x1 - 243,2

Az x1-ben feltételesen tiszta regressziós együttható a pár mindössze 58% -a. A fennmaradó 42% annak a ténynek köszönhető, hogy az x1 variációhoz az x2 x3 tényezők változása társul, ami viszont hatással van az eredményre. A páros regressziók összes jellemzőjének és a páros regressziós együtthatóknak a kapcsolatát a kapcsolati grafikon mutatja be (8.2. Ábra).

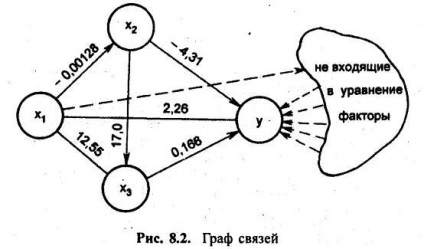
.. Ha összeadja értékelése közvetlen és közvetett hatásait a variációs x1 on y, azaz a termék együtthatók páros regressziót minden „út” (. 8.2 ábra), megkapjuk: 2,26 + 12,55 + 0,166 · (-,00128) · (-4,31) + (-0,00128) · 17,00 · 0,166 = 4,344.

Ez az érték még nagyobb, mint az x1 páros csatolási együttható y-vel. Következésképpen az x1 variációjának közvetett befolyása az egyenletben nem szereplő faktor-tényezőkön keresztül fordított, így összegezve:

3.886 - 4.344 = -0.458.

Tehát, mi tekinthető az értékelés a jelentősége a regressziós koefficiensek és korrelációs Student-féle F-próba, és hozta fel annak fontosságát, hogy a számítás a regressziós koefficiensek és korrelációs Student-féle F-teszt is szerepel az adatokat számolja jelentősége.

A tanulmány csak az összetett probléma legáltalánosabb kérdéseit vizsgálja, és kiindulási ötletet ad a többszörös regressziós egyenlet és a kapcsolódási mutatók előállításának módszeréről.

2 Johnston J. ökonometriai módszerek. - M. Statistics, 1980. - 282 p.

8 Kremer N. Putko B. Econometrics .- M .: UNITY-DANA, 200, - 281p.

[2] Kremer N. Putko B. Econometrics .- M .: UNITY-DANA, 200, p.64

A webhely nagyon hasznos! Vegyünk egy kis szünetet, diák szórakozni: A vizsgán a fizika tanár próbál húzni a pozitív értékelést a gondatlan tanuló: - Meg tudnád nevezni a nevét legalább egy kiváló fizikus? - Persze professzor vagy. By the way, egy anekdota venni a chatanekdotov.ru