Shewhart kontroll diagramok
Töltsd le a jegyzetet Word formátumban. példák Excel formátumban [1]
Röviden. A Shewhart vezérlési grafikon grafikusan megjeleníti a vizsgált folyamatparamétert. A kontroll diagramon a kísérletileg mért értékeket ábrázolják az átlagos, felső és alsó határértékekkel együtt (átlag ± 3 sigma). Ha a folyamat statisztikailag vezérelhető, azaz az eltérés az átlagtól a pontokat csak társított természetes változékonyság rejlő a folyamat, minden pont között helyezkednek a határokat. Ebben az esetben a folyamat javítására irányuló erőfeszítésekre van szükség a változékonyság (a határok közötti folyosó szélessége) és / vagy a középérték csökkentése érdekében. Ha a folyamat jellemzi az ellenőrzés hiánya, azaz bizonyos pontokon kívül az ellenőrzési határok, erőfeszítéseket kell tenni azonosítására különleges okai változékonyság és azok megszüntetésére. Néhány példa a speciális okok variabilitás :. rosszul képzett előadók, hibás tétel alkatrészek, szerszámgép kopását -kár stb Ismét a kontroll térkép azt mutatja, hogy milyen megoldást kell tennie a menedzser: a folyamat javítása vagy megtalálja és megszüntesse különleges oka.
Így a Shewhart ellenőrző kártya egyik feladata olyan helyzetek azonosítása, amelyek jelzik a folyamat statisztikai kontrollálhatóságának hiányát.
És a közelmúltban felbőszült rám! Végül is ezek a kritériumok úgy tűnik, hogy megfelelnek ezeknek az eseményeknek az azonos valószínűségével! Ellenőrizzük.
1. kritérium. A 3-sigma határok egy pontjának hozama jelzi a szabályozhatóság hiányát
Miről beszélünk? Az 1. ábrán. Az 1. ábra 100 véletlen értéket mutat, amelyek közül az egyik a 3-szigma határon kívül helyezkedik el. A rajz egy sor közepes és 3-sigma határt mutat.
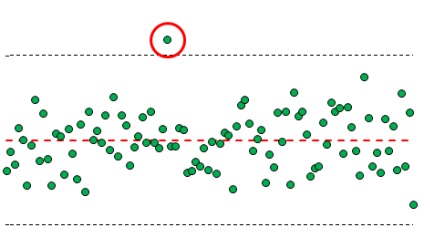
Ábra. 1. Példa egy pont kilépésre a 3-szigma határokon túl
A függvény = NORMSDIST (lásd. Szintén címmel lapot Excel-fájl) konstrukció lemez függően valószínűsége, hogy a valószínűségi változó n -sigmovuyu eltérnénk a szomszédságában az átlagos (ábra. 2), és képviseli a kumulatív valószínűségi eloszlása a valószínűségi változó grafikusan (ábra. 3).
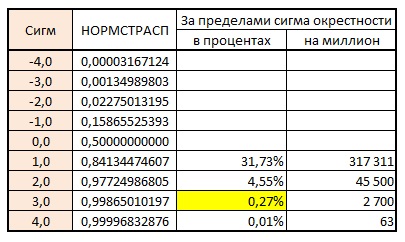
Ábra. 2. A 3-sigma szomszédságon túli kiléptetés valószínűsége
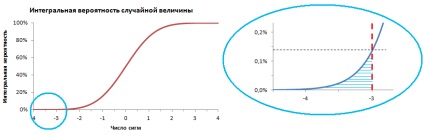
Ábra. 3. Véletlen változó eloszlásának integrális valószínűsége
Az első kritérium relevanciája 99,73%. Ez csak egy valószínűsége 0,27% túlmutató 3-sigmovoy határ nem társul konkrét okokat, és fog irányulni „release” random (statisztikailag ellenőrzött) értékek - téves riasztás.
Egy véletlenszerűen normálisan elosztott mennyiség viselkedésének szimulálására az Excel = NORMSINV (RAND) függvényt használjuk (lásd a "Forrás" lapot). A modellezési folyamat vezérlőkártyája a 3. ábrán látható. 4.
Ábra. 4. A 3-szigma határok elérésének valószínűsége
Az 1. ábrán. 4 az abszcisszán - a sorszám (mindegyik 10 000 érték); az ordinát tengelyén - a valószínűség meghaladja a 3 sigmát. Ehhez a kontroll kártyához az átlag = 0,28%, ami megfelel elméleti 0,27% -osnak. Ha az F9 billentyűt egy Excel fájlban nyomja meg, a térkép kissé megváltozik a szeme előtt.
2. kritérium. A középső vonal egyik oldalán fekvő három egymást követő pont közül legalább kettő a 2-szigma-határértékek esetében a szabályozhatóság hiányára utal
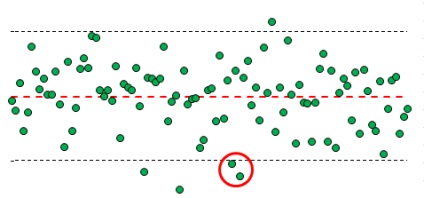
Ábra. 5. Példa a középső vonal egyik oldalán lévő három egymást követő pont közül legalább kettő kimenetére, a 2-szigma határértékek fölött
Térjünk vissza a 2. ábrán lévő táblázatba. 2. A 2-sigmoid szomszédos területen kívül egy valószínűségi változó kimenetének valószínűsége 4,55%. A kilépési valószínűség csak az átlag egyik oldalán (magasabb vagy alacsonyabb) 4,55 / 2 = 2,275%. Annak a valószínűsége, azon túl 2 sigmovoy szomszédságában egyik oldalon a közepén, a két egymást követő pont [2] = (4,55 * 2,275%) = 0,104%. Ha három pontot veszünk fel, akkor a 2-sigmoid szomszédságon kívül két pont egymás után, vagy két pont egymás után kiléphet. Így annak a valószínűsége, hogy legalább két, három egymást követő pont fekvő egyik oldalán a középvonaltól lép túl a sigmovye 2 = 2 * 0,104 = 0,207%.
A szimuláció eredményeit az 1. ábrán mutatjuk be. 6.
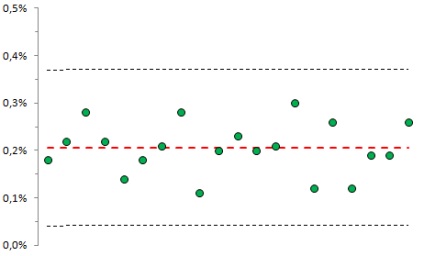
Ábra. 6. A 2-szigma határokon kívül három egymást követő két pont egymás utáni sorozatának valószínűsége
Az 1. ábrán. 6 az abszcissza tengelyen - 20 sorozatban (mindegyik 10 000 érték); az ordinát tengelyen - a háromsoros pont közül legalább kettő, a központi vonal egyik oldalán, a 2-szigma korlátokon túl. Ehhez a kontroll diagramhoz az átlag = 0,205%, amely elméleti 0,207% -nak felel meg.
A második kritérium relevanciája, ami a kontrollálhatóság hiányát jelzi, némileg magasabb, mint az első kritériumnál, és 99,79%. Azaz, a valószínűsége 0,207% hozam túl két-sigmovoy határain legalább két, három egymást követő pontok nem társul konkrét okok, és fog irányulni „ejekciós” véletlenszerű (statisztikailag ellenőrzött) értéket.
A 3. kritérium. A központi vonal egyik oldalán fekvő öt egymást követő pont közül legalább 4 az 1-sigma határok esetében a szabályozhatóság hiányára utal
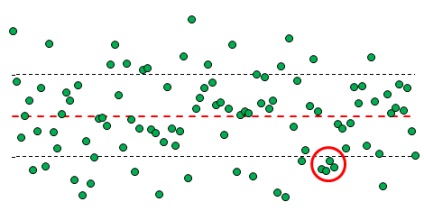
Ábra. 7. Az 1-szigma határon kívül öt egymást követő négy pont négy sorozata
Az ilyen esemény elméleti valószínűségének táblázat alapján történő kiszámítása (2. ábra) nem sikerült. L Látható, hogy az 1-szigma határon túlmutató valószínűségi változó valószínűsége 31,731%. Az 1-sigma szomszédság feletti valószínűség az egymás után négy pont átlagának egyik oldalán 31,731 * (15,866%) 3 = 0,127%. És itt van, hogyan kell kiszámítani a kimenetet, legalábbis. ötből négy egymást követő pont kívül 1-sigmovoy szomszédságában, nem értem ... Különösen figyelembe véve, hogy szükség van, hogy vegye figyelembe a bonyolultabb esetekben, amikor a sorozat tartalmazhat öt, hat vagy annál több pontot ...
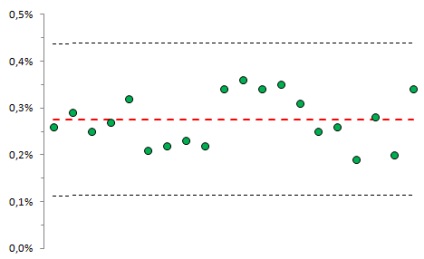
Ezért továbbra is igénybe kell venni a modellezést (8. ábra).
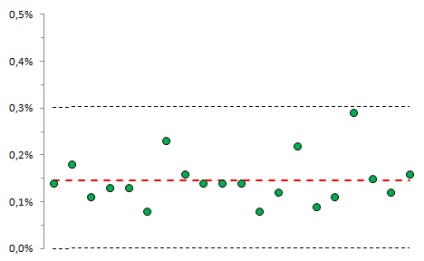
Ábra. 8. A sorozat megjelenésének valószínűsége, amelyben öt egymást követő legalább négy pont túlmutat az 1-szigma határokon
Az ilyen sorozat valószínűsége 0,15%.
A 4. kritérium. A középvonal egyik oldalán legalább 8 egymást követő pont helyzete a szabályozhatóság hiányát jelzi

Ábra. 9. Egy nyolc egymást követő pontsorozat a középvonal egyik oldalán
Az a valószínűség, hogy a véletlenszerûen nyolcszor egymás után véletlenszerû érték az átlag egyik oldalán értéket vesz fel, (1/2) 8 = 0,391%. A modellezés jó példa erre (10. ábra)
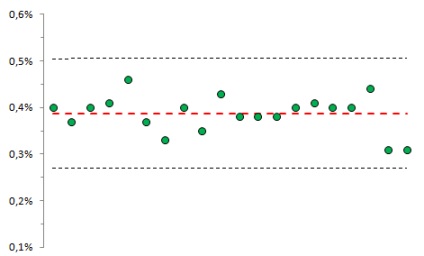
Ábra. 10. A középső vonal egyik oldalán nyolc egymást követő pontsorozat valószínűsége
Az 1. ábrán. 10 az abszcissza tengelyen - 20 sorozatban (mindegyik 10 000 érték); az ordinát tengelyén - legalább nyolc egymást követő pont megjelenésének valószínűsége a központi vonal egyik oldalán. Ehhez a kontroll kártyához az átlag = 0,387%.
Egyetlen táblázatban megkapjuk a kapott adatokat