Segíteni a gouge
Ortogonális transzformációk. Tulajdonuk. Az ortogonalitás koordinátája.
Két-dimenziós euklideszi tér nevezzük izomorfak ha létezik egy-az-egy, lineáris leképezés: ahol (A (x), A (y)) = (x, y) (1) minden x és y.
7. Tétel: Egy euklideszi térnek egy euklideszi térbe való azonos térképezése egy izomorfizmus, ha megőrzi a skaláris terméket.
Ortogonális transzformációk. Az euklideszi tér A átalakulása ortogonálisnak mondható, ha megőrzi a skaláris terméket, azaz ha az (1) feltétel bármelyik vektorra érvényes A 7. tételből következik, hogy egy ortogonális transzformáció isomorfizmus önmagára.
8. Tétel: Ha az átalakulás ortogonális, és csak ebben az esetben a konjugált transzformáció az inverz.
Valóban, az alábbi képlet szerint (1), van (x, A * A (y)) = (x, y) vagy (x, A * A (y) - v) = 0. Ez azt jelenti, hogy a vektor A * A ( y) -y ortogonális bármely térbeli vektorra, és következésképpen nulla. Mivel az A * A (y) = y egyenlõség mindegyik y esetében érvényes, az A * A transzformáció az identitás, amely megfelel a bizonyítéknak. Ezzel szemben könnyen beszerezhető (1) az A * A = E egyenlőségtől.
Tétel 9. Egy transzformáció ortogonális, ha és csak akkor, ha bármelyik ortonormális bázis mátrixa ortogonális.
Ez közvetlenül az A * = és a Proposition 8 képletből következik.
10. Tétel: Két ortonormális b és e alapon létezik egy egyedi ortogonális transzformáció, amelyre A () = (i = l, N).
Bizonyítás. Az e-f. létezik és egyedülálló: az e alap mátrixa a vektorok koordináta oszlopaiból áll. a alapján e. Transzformáció egy ortogonális, mint a mátrix egy ortonormáiis bázis ortogonális (ez az átmenet mátrix e f).
11. tétel. Az ortogonális transzformáció abszolút értékének sajátértékek egyenlők.
Valójában minden x-sajátvektor esetében van (A (x), A (x)) = (x, x) és (A (x), A (x)) = (x, x). Ezért = 1.
12. Tétel


Tény, hogy egy ortogonális transzformáció egy-egy, ezért minden alrendszert ugyanabba a dimenzióba tartozó alrendszernek veszi. mert



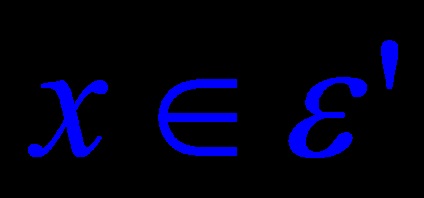
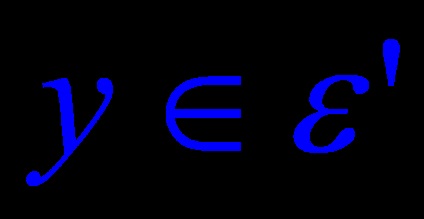





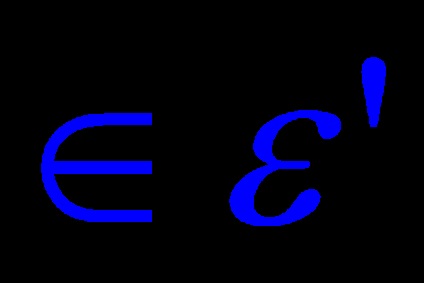
Tétel 6. Legyen A egy n-dimenziós euklideszi tér ortogonális átalakulása. Ezután a páronként ortogonális egydimenziós és kétdimenziós szubpóderek közvetlen összege invariáns az A alatt.
A bizonyítás érdekében indukciót használunk. Az 1. és 2. méretű terek esetében az állítás nyilvánvaló. Tegyük fel, hogy bizonyítottuk a k-1 és k-2 méretintervallumok tételét, és k-dimenziós térre igazoljuk. A 8. javaslathoz kapcsolódó következményekkel
Van egy egydimenziós vagy kétdimenziós invariáns szubtér. Az ortogonális komplementuma a k-1 vagy a k-2 invariáns alrendszere. Az A transzformáció korlátozására az indukciós hipotézist alkalmazzuk. Altér. amelyen bomlik, az A-val szemben invariáns.
dim = dim + dim. Az indukciós hipotézis szerint dim = dim +. + homályos. Így, a subspace-ekhez. az összeg dimenziója megegyezik a dimenziók összegével, és következésképpen az összeg közvetlen. A tétel bizonyított.