Az összes erőt a lejtő lejtőjén tervezzük
A lejtők és a lejtők stabilitása
A fejlesztés a gödrök, területeken, ahol a függőleges elrendezés szegélyek, barázdák és dombok eszköz, emelt lejtőkön, más esetekben meg kell becsülni talajellenállást tömbök lejtőkön. A sekély lejtők építése drámaian megnöveli az építési költségeket. A meredek lejtők balesethez vezethetnek. Meg kell találni a lejtők optimális meredekségeit vagy a tervezőfalakat.
A stabilitási pályák elvesztésének okai:
- a talajvíz természetes támogatásának megszüntetése árkok, árkok, stb. fejlesztése miatt;
- a meredekség külső terhelésének növekedése;
- a talaj fajsúlyának növelése az összeomlási prizmában a víz pórusainak telítettségének eredményeként;
- a kapilláris nedvesség hatása, ha a vízasztal leereszkedik;
- A talaj tapadásának és súrlódásának csökkentése a talaj nedvesítése, fagyása és felengedése közben;
- dinamikus hatások (forgalom, szeizmikus megnyilvánulások);
- nagy meredek meredekség.
A talaj tömegének megsértése hirtelen előfordulhat jelentős talajtömegek csúszásával. Az ilyen egyensúlytalanságokat földcsuszamlásnak nevezik. A földcsuszamlások a következő típusokból állnak:
a) forgásirányú földcsuszamlások (görbült összeomló felületekkel);
b) csúszásmentes földcsuszamlások (rögzített felületeken);
c) A cseppfolyósodás (ún. túltelített víz sápadtá válása a talajban).
4.5.1. Az ideálisan laza talaj lejtői stabilitása (с = 0, j00)
Tegyük fel, hogy a meredekséget alkotó homok belső súrlódási j szögének adott értékével rendelkező lejtési szöggel rendelkező dőlésszög van.
Tekintsük a talaj M részecskéjének egyensúlyát, amely szabadon fekszik a lejtő felszínén (4.13. Ábra, a). A P-részecskék súlyát a szokásos N-re bontjuk az ab vonalra és a T érintőre. A részecske lefelé mozgatására törekszünk. A talajnak csak belső súrlódása van, így a részecske stabilitása akkor biztosítható, ha a T nyíróerő egyenlő vagy kisebb, mint a súrlódási erő T '= fN.
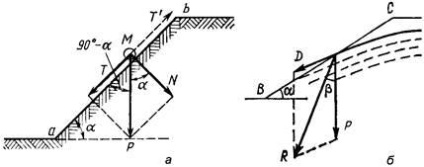
Ris.4.13. A laza talaj lejtői stabilitásának kiszámítására szolgáló rendszer:
a - száraz; b - víz szűrése
Az összes erőt a lejtő lejtőjén tervezzük
Ezért tga = f. de mert súrlódási tényező f = tgj, akkor megkapjuk az a = j értéket. Következésképpen a szabadon folyó talajok lejtésének határszöge megegyezik a belső súrlódás szögével. Ezt a szöget a természetes lejtés szögének nevezik.
A meredekség stabilitásának biztosítása érdekében az M részecskét megtartó erőnek nagyobbnak kell lennie, mint a nyíróerő: TT '. A megbízhatósági tényezőt tekintjük gn. akkor gn tga £ tgj. Általában a gn-t 1.1¸1.2.
Ha a talajvíz szintje a laza talajok egy csoportjában a lejtő alja felett van, a lejtő felszínén szűrőáram jelenik meg. A talajban megjelenik a hidrodinamikai nyomás, ami a lejtő stabilitásának csökkenéséhez vezet. Ezért, figyelembe véve az M részecskék egyensúlyát a lejtős felületen, meg kell adni a nyíróerőnek a hidrodinamikai komponenst
ahol gw a víz fajsúlya; n a talaj porozitása, i a nyomás gradiens.
A vízkivezetés pontjánál a D és P erők a lejtőfelületen hatnak keresztül, és a kapott R értékre kerülnek. Ebben az esetben a meredekség szögének stabilitása az állapotból származik
4.5.2. A talaj függőleges lejtésének stabilitása, amely csak kohézióval rendelkezik (j = 0, c00)
Az ilyen talaj esetében vegye fontolóra a függőleges meredekség ab értékét (4.14. Ábra). Húzza le a lehetséges csúszófelület a vonalát a szögben a a horizonton. Ezen a síkon keresztül a speciális tapadási erők fognak hatni.
Tegyük fel a csúszó prizma abc-re ható erők egyensúlyának egyenletét. A cselekvõ erõ a prizma abc P súlya.
Figyelembe véve, hogy bc = h ctga, akkor megkapjuk
A P erővel az N normál komponensekkel és a T érintőkkel a csúszó felületre ac. Azok a csapatok, amelyek ellenállnak a csúszásnak, csak kohéziós erők leszek. a csúszó sík mentén elosztva.
Mivel a prizma abc felső pontján a nyomás nulla, az alsó pedig a legnagyobb, akkor a kohéziós erőknek csak a felét kell figyelembe venni.
Tegyük az egyensúlyi egyenletet, és vesszük az összes erő előrejelzésének összegét az ac irányba, és egyenlővé tesszük nullával:
Határozzuk meg a h = h90 magasságot. amely megfelel a tengelykapcsoló erők maximális használatának. Nyilvánvalóan itt sin2a = 1, a = 45 0. Ezután a sin2a = 1 értéket a 4.35-ös kifejezéssel helyettesítve és a h90-re vonatkoztatva megoldva. kapunk
A gn megbízhatósági tényezővel rendelkezünk
Ebben az esetben h a lejtés maximális lehetséges magassága rögzítés nélkül.
4.5.3. A lejtők stabilitása az egyensúly korlátozásának elméletében
A belső súrlódással és kohézióval rendelkező talajok esetében V.Sokolovsky két problémát megoldott:
1. A talaj tömegének vízszintes felületére vonatkozó maximális nyomás meghatározása, amelyen a vázlat vázlata egyensúlyban marad.
2. A határoló meredekség egyforma stabil lejtése alakjának meghatározása.
A belső súrlódás j különböző szögeinek és a lapos dőlésszögnek az a horizontra történő dőlésszögének szögszegmensére vonatkozó differenciálegyenletek differenciálegyenletek numerikus integrálásánál megtalálhatóak a P határértékek:
ahol a korlátozó nyomás dimenzió nélküli értéke (III. melléklet III.5. táblázat) j, a és relatív koordináták függvényében kerül elfogadásra:
Az egyenletesen stabil lejtés körvonalait felépítik, kezdve a felső élével.
Egy egyenletesen egyenletes vízszintes felület egy egyenletesen elosztott terhelést hordozhat
Ha P0 a P0 = gh talajréteg nyomásának tekintendő. az
4.5.4. A meredekség stabilitása körkörös hengeres csúszófelületek hozzávetőleges módszerével
Ez a módszer, amelyet a gyakorlatban széles körben alkalmaznak, először K. Peterson 1916-ban alkalmazta és sokáig "a svéd geotechnikai társadalom módszere" -nek nevezték. A módszer alkalmazásának lényege a következő: Állítsa a forgásközéppontot AB AB meredekségéről. Az egyensúly egyenlete SM0 = 0. A készítmény pillanatok egyenletet képest elfordulás O osztott prizma csúszási pont ABC függőleges keresztmetszeteket be számos rekeszt, és mindegyik rekeszben tömeg fogadja feltételesen tömeg alkalmazni a metszéspontja Pi rekeszt egy megfelelő csúszó ívszakasz. Elbontjuk Pi súlyerő az irányt az elforgatás sugarának és a rá merőleges (ris.4.17 a) és össze egyensúlyi egyenlettel egyenlővé nullára a pillanatban ható erők pivot pont:
Ezt a kifejezést R. által megszabadítjuk
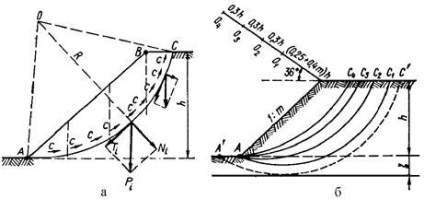
ahol L az ív hossza; c. j - belső súrlódási és tapadási erő szöge; Ti és Ni értékei a súly erősségének és normál összetevői. .
Ris.4.17. A lejtők stabilitásának kiszámítására szolgáló rendszerek körkörös hengeres csúszási felületeken: a - az erők hatásának rendje; b - veszélyes csúszó ívek helyzete
A lejtés stabilitási együtthatója esetében a pillanatnyi nyomatéki erők erőinek pillanatát kell figyelembe venni:
Meg kell választani a legveszélyesebb csúszófelületek minden lehetséges ívét (4.17, b ábra). Az O1 ívek tervezett központjaira. O2. O3 meghatározzuk az összekapcsolást, amely szükséges a stabilitási körülményhez, amely megfelel az egyensúlyi egyensúlynak,
A lehetséges csúcspontok közül kiválasztjuk azt, amelyre a kohéziós erők maximális értéke szükséges. A h stabilitási együttható értéke 1,1 ... 1,5. Ezt a módszert az MNGol'dshtein és a GI Ter-Stepanian finomította:
ahol A és B az együtthatók (III. melléklet III. 8. táblázat, 8. példa), táblázatosan a töltés m és x = (0,25, 0,5, 1,0, 1,5) h
4.5.5. A lejtős lejtők és lejtők stabilitása
A lejtős lejtés stabilitását az egyensúlyi egyenletek határozzák meg. Ebben az esetben a talajtömeg több részre van felosztva, így az egyes rekeszekben a csúszófelület lapos, és sűrűbb, zavartalan sziklák rögzített felületén halad (4.18.
Ris.4.18. Az erők rendszere a földcsuszamlás nyomásának meghatározásakor
Figyelembe véve az i-os rekeszt, vegye figyelembe az összes külső erőt, beleértve a terem felületére ható terhelést és a talaj súlyát a rekesz térfogatában. A Qi külső erők összege egy normál Ni-hez és egy Ti érintőhöz lesz bontva. A normál Ni erő lehetővé teszi, hogy figyelembe vegye az súrlódási erőket az nm-ben. Ezenkívül a tapadási erőket a sík mentén vett ollóknál figyelembe veszik. Ezenkívül a túlnyúló Ei-1 rekeszek kiegyensúlyozatlan földcsuszamlásának nyomása és az Ei alsó rekeszben ismeretlen földcsuszamlás hatása a rekeszre hat. Ha a lejtés még mindig olyan szeizmikus erők hatása alá esik, amelyek a külső erők eredményét a függőleges irányból bizonyos szögű qi irányba tolják. akkor kapunk
Az egyensúly egyenleteivel - az összes erő előrejelzésének összegével az nm irányba és a normál irányba - az Ei értékcsökkenési érték értékét találjuk. továbbítani a következő rekeszbe:
ahol h a stabilitási együttható.
A számítás az első felső rekesszel kezdődik, amelynél Ei-1 = 0. A rekesztől a rekesz felé haladva az utolsó rekesz elérte az eredményt, amely stabilnak kell lennie En £ 0-ra.
4.5.6. A földcsuszamlások elleni küzdelemről
A földtömegek stabilitásának megsértését az utak, a hidak, a lakóépületek és az ipari épületek megsemmisítése kísérte, néha emberi áldozatokkal.
A szárazföldi tömegek stabilitásának növelésére és a földcsuszamlás elleni küzdelemre irányuló intézkedések a következők:
- a kúszó tömegek természetes megállásának helyreállítása és megerősítése;
- a talajtörés vízszabályozásának szabályozása;