A rendszer csillagképes poliéderje - tudd meg! Dodecahedron - hogyan lehet a megfelelő dodecaédert létrehozni
A csillag-oktaéder nyolc tetszőleges tetrahedron formájában volt egymáshoz kapcsolva.
Majd majdnem 100 évvel később a poliéderet újra feltárta Johannes Kepler, akit Stella oktanulának neveztek, nyolcszögletű csillagként.
Ez az illusztráció egy csillag-oktaédron, amely vitát vált ki arról, hogy ezt a poliédert felfedezték.

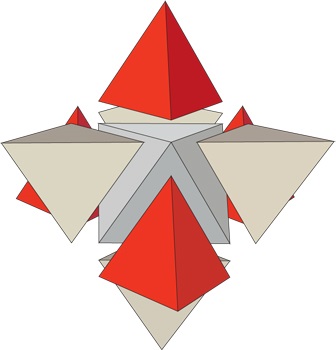
Az első lehetséges változat az oktaéder 8 tetrahedrák oldalához való kötődés
Vagy az oktaéderek oldalaival párhuzamos síkok folytatása, miután a síkok metszéspontjában ugyanazt a 8 tetrahedrát kaptuk. Más szóval, egy csillag alakú oktaéder létrehozásához.
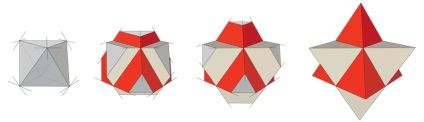
A második út: Két tetraéder kombinálása.
Ami grafikusan illusztrálja az arcok színét két színben - piros és bézs.
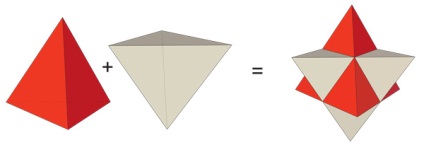
1. A polyhedron az oktaéder egyetlen csillag alakú formája.
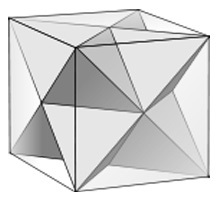
2. A poliéder érdekes tulajdonsága. Ha minden csúcspontot összeköt, akkor a keresztezési vonalak pontosan megfelelnek a kocka éleinek.
Így egy csillag-oktaéder lehet beilleszteni egy kockába.
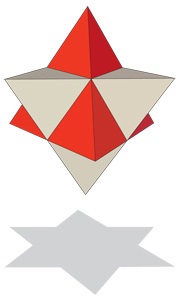
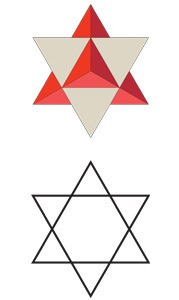
3. Ha a felülről vagy a csepp árnyékból nézzük meg a poliédert, a kép körvonalai létrehozzák a megfelelő hatszögletű csillagot.
Hatágú csillag formájában két, egymást keresztező háromszög egy ősi szimbólum, amely a továbbiakban a Dávid-csillag (más néven - a Seal of Solomon).
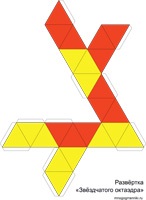
A javasolt összeszerelési lehetőségek közül az első az, hogy a csillagok oktaéderét egyetlen söprésből ragasztják be. Ez a lehetőség leggyakrabban az oktatási szakirodalomban található meg. Azonban a korlátozás a lap mérete. Ha ez egy A4-es lap, akkor a kész poliéder méretei nagyon szerények.
A második lehetőség, ha külön összeállított oktahedron és 8 üres piramis formában. Ezután minden üresen ragasztják az oktaéder oldalára. Ez az opció előnyösebb a kezdő modellezők számára.
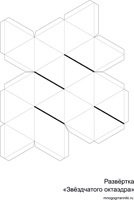
Az interneten találkoztunk egy nagyon szokatlan változattal a gyülekezés, valamint egy sweep.

A rombusz-csonkolt icosa-dodekaéder

A rombusz-csonkolt icosa-dodekaéder egy félvérű konvex poliéder, amelynek két tulajdonsága van:
1. Az összes arc három típusból álló rendszeres sokszög - egy dekagon, egy hatszög és egy háromszög;
2. Minden csúcspár esetében van egy szimmetriája a poliédernek (vagyis egy mozgásnak, amely magában foglal egy poliédert), amely egy csúcsot vesz fel a másikhoz.
Archimedesi szilárd anyagok semiregular poliéder abban az értelemben, hogy élek - szabályos sokszögek, de nem azonos a jelen esetben az a feltétel, az egyik térbeli szimmetria típusok: tetraéder, oktaéder vagy ikozaéder.
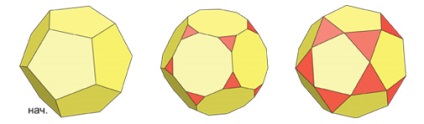
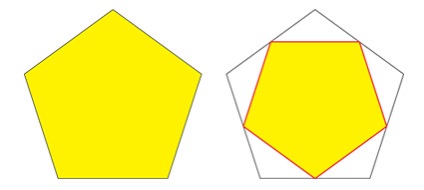
A dodekaéder eredeti oldala megtartja ötszög alakját, de a négyzetben elveszíti a felületét.
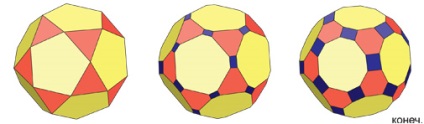
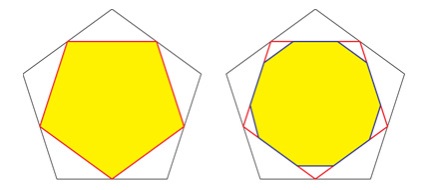
Az eredeti dodekaéder oldala, az előző átalakulástól eltekintve, elveszíti a szögét, és 10-esre változik.
A modell elkészítéséhez a következő részletek szükségesek:
- 12 db. a dekagon
- 20 db. hatszög
- 30 db. terek
Maga is létrehozhat egy polyhedron modellt, normál geometriai alakzatokkal, vagy lapok számokkal - színes beolvasással. Ehhez 3 A4-es lapra van szükség


Csonka icosahedron
Egy poliéder kapható az ikozaéder mindegyik csúcsainak egymás után történő vágásával.

A csonka icosahedron egy semireguláris konvex poliéder, amelynek két tulajdonsága van:
1. Az összes arc rendszeres kétszemélyes poligon - egy hatszög és egy ötszög;
2. Minden csúcspár esetében van egy szimmetriája a poliédernek (vagyis egy mozgásnak, amely magában foglal egy poliédert), amely egy csúcsot vesz fel a másikhoz.
Archimedesi szilárd anyagok semiregular poliéder abban az értelemben, hogy élek - szabályos sokszögek, de nem azonos a jelen esetben az a feltétel, az egyik térbeli szimmetria típusok: tetraéder, oktaéder vagy ikozaéder.



Ennek a poliédernek az a fő jellemzője, hogy formája szolgál alapul a futballlabda gyártásához. Ez nyilvánvalóvá válik az arcok színének fekete-fehér verziójának alkalmazása után.
Az icosahedron mind a 12 csúcsának csonkítása egy csonka icosahedron kialakulásához vezet. Az eredeti poliéder háromszög alakú arcai elveszítik a területet, és hatszögletű arcokká alakulnak át.
Az ábra egy csonka ikozaéder kibontakozását mutatja:
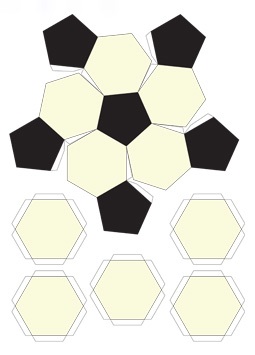
Ebben az esetben nem hoztunk minden részletet egyetlen szkenneléssel, mintha kinyomtatható egyetlen A4, a végső mérleg gyűjtött adatokon lesz nagyon kicsi.
A modell elkészítéséhez letöltheti a lapolvasást pdf formátumban és nyomtathatja két A4-es lapra. Kérjük, vegye figyelembe, hogy a lapok megegyeznek!
A sweep a foci labda klasszikus színezésének megfelelő színben készült.
Csonka dodekaéder
Egy poliéder állítható elő egy dodekaéder csúcsainak egymás után történő vágásával.

A csonka icosahedron egy semireguláris konvex poliéder, amelynek két tulajdonsága van:
1. Minden arc rendszeres kétféle poligon - egy decagon és egy háromszög;
2. Minden csúcspár esetében van egy szimmetriája a poliédernek (vagyis egy mozgásnak, amely magában foglal egy poliédert), amely egy csúcsot vesz fel a másikhoz.
Archimedesi szilárd anyagok semiregular poliéder abban az értelemben, hogy élek - szabályos sokszögek, de nem azonos a jelen esetben az a feltétel, az egyik térbeli szimmetria típusok: tetraéder, oktaéder vagy ikozaéder.
A dodekaéder mind a 20 csúcsának csonkolása egy csonka dodekaéder keletkezését eredményezi. Az eredeti poliéder pentagonális arcai elveszítik a területet, és dekagonális arcokká alakulnak át.
Az ábra egy csonka dodekaéder kibontakozását mutatja:
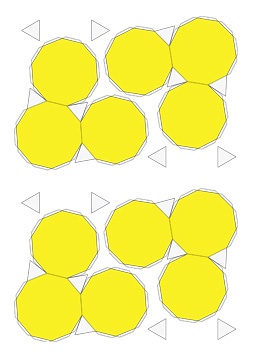
Ebben az esetben nem hoztunk minden részletet egyetlen szkenneléssel, mintha kinyomtatható egyetlen A4, a végső mérleg gyűjtött adatokon lesz nagyon kicsi.
A modell elkészítéséhez letöltheti a lapolvasást pdf formátumban és nyomtathatja két A4-es lapra. Kérjük, vegye figyelembe, hogy a lapok megegyeznek!
- Ha színes nyomtatóra kíván nyomtatni - színes beolvasást
- ha színes kartonpapírt kíván használni: töltse le a szkennelést