Számtani műveletek a bináris rendszerben - stadopedia
A helymeghatározó rendszerek közül a bináris jelölés különösen egyszerű. Fontolja meg az alapvető számtani műveletek végrehajtását bináris számokon.
Minden helymeghatározó rendszer "ugyanaz", azaz mindegyikben a számtani műveleteket ugyanazon szabályok szerint végezzük:
Ugyanazok az aritmetikai törvények igazak: kommutatív, asszociatív, disztributív;
Az oszlopra vonatkozó kiegészítés, kivonás és szorzás szabályai érvényesek;
a számtani műveletek elvégzésére vonatkozó szabályok az addíciós és szorzótáblákon alapulnak.
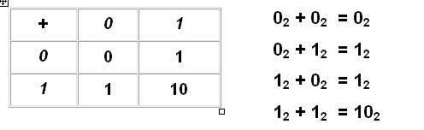
Vegyünk példákat a kiegészítésre.
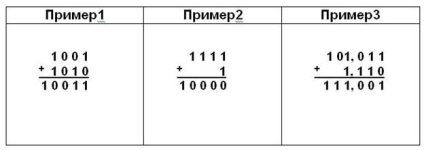
Amikor két számot hozzáad a jobb oldali bináris rendszerben, mint bármelyik pozíciós rendszerben, csak az egyik a következő számjegyre tud átmenni.
A két pozitív szám beadásának eredménye vagy ugyanannyi számjegyet ad meg, mint a két summán vagy egy számjegy maximális, de ez csak egy lehet.
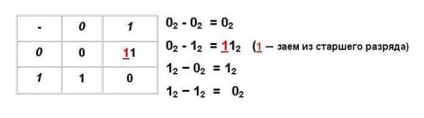
Vegyünk példákat a kivonásra.
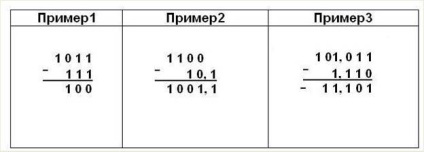
Csökkentési művelet végrehajtásakor mindig a kisebb számot abszolút értékből kivonják a nagyobbakból, és a megfelelő jel kerül az eredményre.
Vegyünk példákat a szorzásra.

A szorzás művelete a szimulációs táblázat alapján történik (a decimális rendszerben használt), a következő számjegy szorozva a tényező egymást követő szorzásával.
Vegyünk példákat a szorzásra.
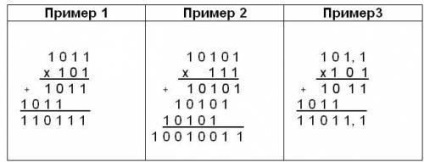
A 2. példában szereplő szorzások végrehajtásakor három 1 + 1 + 1 = 11 egységet adunk hozzá a megfelelő 1-es számjegyhez, a másik pedig a legmagasabb számjegyre kerül.
A bináris rendszerben a szorzási művelet a szorzás fordítására és a köztes eredmények hozzáadására korlátozódik.
A megosztási műveletet egy algoritmussal végezzük, amely az algoritmushoz hasonlóan elvégzi a szétválasztás műveletét a decimális számrendszerben.
Vegyünk példákat a felosztásra
