Nem reális áramlási struktúrájú rektori modellek
A reaktorok elméletében olyan modelleket fejlesztettek ki, amelyek lehetővé teszik az áramlás tökéletlenségeinek figyelembe vételét. Ezek a modellek is hozzávetőlegesek, de pontosabban leírják az igazi folyamatot, mint az ideális keverés vagy elmozdulás modellek.
A valós reaktorok matematikai modelljei két megközelítés alapján épülhetnek fel.
Egy valódi reaktor mentális helyettesítésén alapul, amely ideális eszköz egy vagy másik kombinációjával.
Matematikai leírás összeállításakor megpróbálják figyelembe venni a készülékben előforduló valódi fizikai jelenségeket, és bevinni őket a modell egyenletébe.
Az első megközelítésben a matematikai modell egy olyan egyenletrendszer, amely egyesíti az ideális reaktorok matematikai leírását. Az egyenletek száma nagy lehet, de szerkezetükben annyira egyszerűek, mint az ideális modellek egyenletei.
A második megközelítésben az egyenletek száma lehet kisebb, de összetettebbek és ennélfogva bonyolultabb megoldási módszerek.
A legtöbb ipari reaktorokban működik Cha-részecske vagy helyi a reagensek összekeverése a reakciótermékek, azaz. E. reaktorral néhány valódi-ing köztes helyzetben a reaktorok a teljes keverési és ideális elmozdulás. Az ilyen reaktorokat pontosan leírták az úgynevezett diffúziós modell.
Diffúziós modell. Ez a modell matematikailag kifejezhető egyenletek által, amelyek figyelembe veszik a változás a koncentráció nem csak a kémiai átalakítás (mint egy ideális kiszorítják-nenii), hanem eredményezi néhány a reagensek összekeverése és a reakció miatt a termékek molekuláris vagy turbulens diffúziós, -sion. A diffúziós modell leírható az ideális elmozdulás modelljével olyan kifejezések bevezetésével, amelyek figyelembe veszik a megfelelő fáziskeverést az igazi készülékben.
A radiális keverés vízszintes (elemi) rétegben sima, hőmérsékleti és vezetési mezőket sima, és az egyes részecskék tartózkodási idejét igazítja. Így a radiális keverés mindig hasznos, és kevés hatással van a reaktor modellre. Ezért a diffúziós modell egyenletét általában egypéldányos formában írják, figyelembe véve a hosszirányú szállítást. Az n-edik megbízás irreverzíbilis kémiai reakciója, egyensúlyi állapotban (egyensúlyi állapotban) van kialakítva
ahol DL a hosszirányú keverési együttható, amely egyenlő a tényleges diffúziós együtthatóval.
Kényelmes dimenzió nélküli formában ábrázolni egy új l-x / L változó bevezetésével, ahol L a reaktor hossza. akkor x = lL, dx = Ldl. Figyelembe véve a kapcsolatot
L / ω,
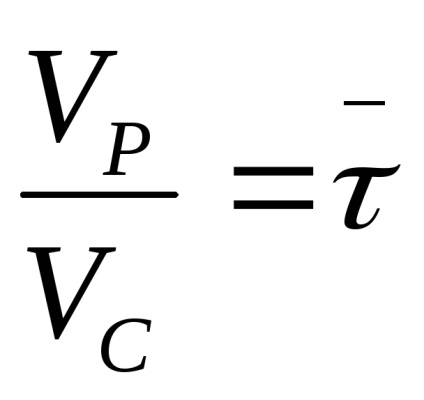
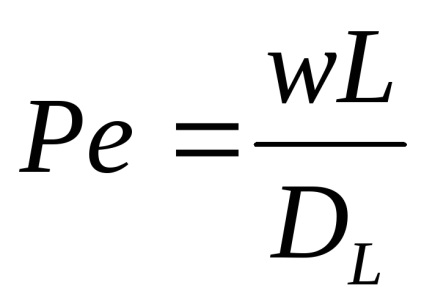
A dimenzió nélküli formában az egyenletet írjuk
Az egyenlet bizonyos határfeltételekkel és rendszerint számítógéppel megoldható. Fedezi a rejtett reaktorok teljes körét, amelyek stagnáló zónák nélkül működnek és elkerülik a reagenseket. Ha Fe = 0
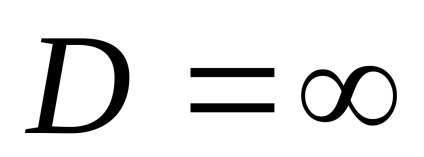
Az elsőrendű reakció esetében a differenciálegyenlet megoldása a következő eredményt hozza:
,
A reaktor magasságának változása a különböző Peclet számokon (1. ábra) megerősíti ezt a pozíciót.
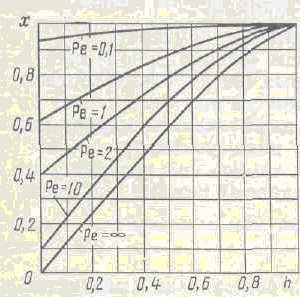
1. ábra. Az x anyag átalakulásának mértékében az izotermikus reaktor magasságához viszonyított változás függvénye a Fe
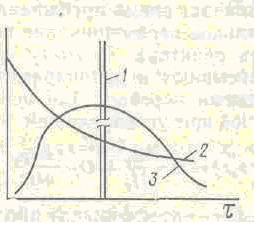
2. ábra. A különböző típusú reaktorokban fellépő impulzus zavarokra adott válasz görbéi:
1 - ideális elmozdulás; 2 - teljes keverés; 3 - önkényes mód
Az egyparaméteres diffúziós modell által leírt reaktorok tartózkodási időeloszlási funkcióinak kiszámítása a reaktor kimenetén a mutató koncentrációjának kiszámításán alapul. Ehhez meg kell oldani a diffúziós modell differenciálegyenletét a nem statisztikai rendszerben anélkül, hogy figyelembe kellene venni a kémiai reakciót
Egy cellás modellben egy valódi eszköz mentálisan feldarabolt N egymást követő összekapcsolt, ideális keverésű sejtekre.
Az összes sejt teljes térfogata megegyezik a reaktor teljes térfogatával.
Az ilyen helyettesítő érvényes a következő okok miatt: 1) a kaszkád reaktor N = 1 - egyetlen reaktorban a tökéletes keveredés, és ha n = ∞ és infinitezimális összegeket szakaszok degenerates egy fojtott áramlású reaktorban.
Így az ideális keverőreaktorok kaszkádjának modellje segítségével leírhatjuk a korlátozó hidrodinamikai rendszereket. És az igazi reaktorban van egy közbenső mód, amelyet le lehet írni az N-sejtekből álló RIS kaszkád modell alkalmazásával, ahol N