Torzítási együtthatók
A koordináta-tengelyek szegmensének torzulását, amikor azokat egy képsíkra vetítik ki, az axonometrikus tengelyek torzulási együtthatói jellemzik.
A torzítás együtthatója a tengely szegmensének és a természetes hosszúságának axonometrikus vetületének hossza.
Az O o x o, O o o o és O o z o tengelyek mentén a torzítási együtthatók:
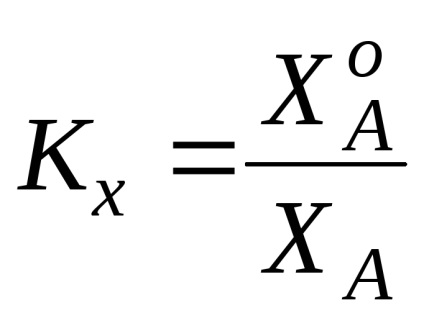
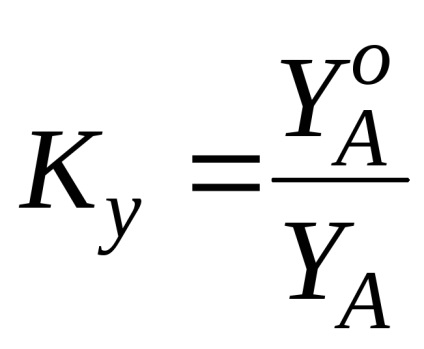
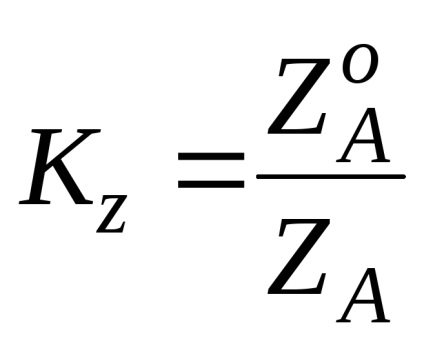
Az axonometrikus vetületek típusai
Vesz egy másik kölcsönös megegyezés természetes koordináta-rendszerben és a képsík és meghatározzák a különböző vetítési irány, akkor lehet kapni több axonometrikus nyúlványok egymástól eltérő irányba axonometrikus tengelyek és e tengelyek nagyságának torzítás együtthatók. A torzítási együtthatók arányától függően:
- ISOMETRIKUS PROJEKCIÓ ("izos" egyenlő), ha a torzulási együtthatók mindhárom tengelyen megegyeznek önmagával:
- DYMETRIC PROJECTION, ha a két tengely torzulási együtthatója megegyezik egymással, és a harmadik esetében az első kettőtől eltérő, például:
- TRIMETRIC PROJECTION, ha mind a három torzulási együttható a tengelyek mentén különböző:
Attól függően, hogy a kifelé irányuló irány és a kép síkja milyen szögben van,
- téglalap alakú axonometrikus vetület. ifs ;
- ferde axonometrikus vetület. eslis
Standard axonometrikus vetületek
A sok lehetséges típusú axonometrikus előrejelzések GOST 2.317- (ST SÜV 1979-1979) javallott a rajzokat és az építőiparban korlátozva, hogy kevésbé torzított kép geometrikus formák és a leghasznosabb az építőiparban.
Négyszögletes axonometrikus előrejelzések és tartalmazzák izometrikus és dimetric vetülete a ferde - frontális és horizontális izometrikus vetítés és az első vetítés dimetric.
A mérnöki ipar rajzaiban a téglalap alakú izometria és a dimetria, valamint a ferde frontális dimetria is szélesebb körben használatos.
Az axonometrikus vetületek minden típusát két paraméter jellemzi: az axonometrikus tengelyek iránya és a tengely mentén a torzítás együtthatói.
Négyszögű izometrikus vetület
A téglalap alakú axonometrikus perspektivikus nézete a tengely O O X o, o o y o o z o iO képest szögben helyezkedik el 120 egymáshoz, vagy, hogy a kényelmes nyomon követésére, szöget képez a 30 ° a vízszintes vonal (ábra. 10).
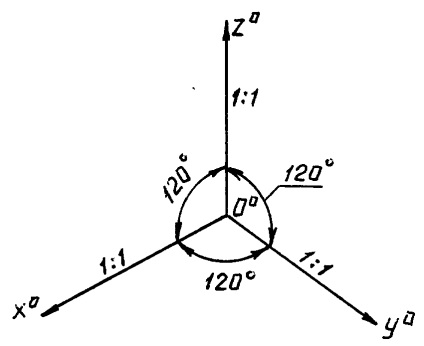
Téglalap alakú axonometriában a torzítási együtthatók négyzetének összege két,
3K2x = 2, amelyből a tényleges torzítási együtthatók a tengelyek mentén azonosak
Mivel ezek az értékek kényelmetlen számlálására méretek konstrukciójánál, a standard javasolja izometrikus nézet torzítás nélkül a tengelyek, amely megfelel a csere a valós együtthatók torzítás kényelmesebb csökkentett együtthatók értéke egy:
Ebben az esetben a kép 1,22-szeresére nő (1 / 0,82 = 1,22).
Négyszögű izometria akkor alkalmazható, amikor az objektumnak az axonometrikus képen látható három oldalának megközelítőleg azonos számú jellemzője van a megjelenített objektum jellemzéséhez.