Frakcionális lineáris függvény egy leckében egy matematikai oktatóval
Idővel a matematika oktatója azzal a hozzáértéssel jön, hogy egyszerűsített nyelven megmagyarázza a komplex fogalmakat, nem pedig a matematikai teljesség és pontosság rovására. Az anyag, a beszéd, a vizuális kíséret és a rekordok rögzítésének egyéni stílusát fejlesztették ki. Bármely tapasztalt oktató szemmel le fogja zárni a leckét, mert előzetesen tudja, milyen problémák merülnek fel az anyag megértése és a megoldásuk megoldásához. Fontos megtalálni a helyes szavakat és feljegyzéseket, példákat a lecke indítására, középre és végére, valamint helyesen fogalmazza meg a házi feladat gyakorlatait.
A témával kapcsolatos néhány speciális módszert tárgyalunk ebben a cikkben.
Néhány grafikon építése matematika oktatót kezd?
Meg kell kezdeni a vizsgált fogalom meghatározását. Emlékeztetem Önöket arra, hogy az űrlap egy funkcióját frakcionális lineáris függvénynek nevezik. Konstrukcióját a leggyakoribb hiperbola felépítésével, a grafikonok transzformálásának egyszerű módszerével redukálják.
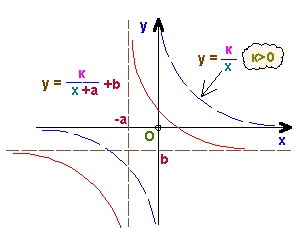
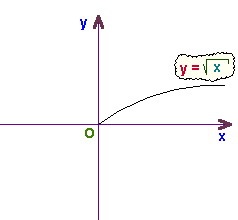
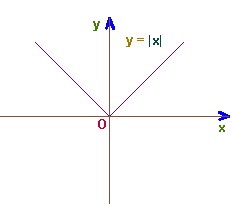
Tehát az oktatónak nincs semmi kényelmesebb és hatékonyabb módja, mint hogy hogyan lehet felkészülni az átalakításra egy négyzetgyök segítségével. Szükséges ilyen típusú diagramokat készíteni. Megfontoljuk, hogy ez az előkészítés sikeres volt. A gyerek elmozdulhat, sőt tömörítheti / nyújthatja a grafikát. Mi következik?
Továbbá érdemes felidézni, hogy a közvetlen arányosság hogyan néz ki, és melyik negyedikben helyezkedik el a grafikon, a k koefficiens jeleitől függően.
A következő lépés az egész rész kiosztásának tanítása. Talán ez a fő feladata a matematika oktatónak, hiszen az egész rész kiválasztása után az egész számítási terhelés oroszlánrészét a témában veszi át. Rendkívül fontos, hogy előkészítse a funkciót egy olyan nézethez, amely illeszkedik az egyik standard konstrukciós rendszerbe. Az átalakítások logikájának érthető módon történő leírása is fontos. másrészt matematikailag pontos és rendezett.
Hadd emlékeztessem önöket arra, hogy a grafikon felépítéséhez át kell alakítani a frakciót az űrlapra. Ez az, hogy nem
, megtartva a nevezőt. Miért? Nehéz elvégezni a grafikon átalakítását, amely nemcsak darabokból áll, hanem aszimptoták is. A folytonosságot két vagy három többé vagy kevésbé érthetően mozgó pont összekapcsolására használják egy sorban. Folyamatos funkció esetén nem fog azonnal megérteni, mely pontokat kell csatlakoztatni. Ezért a hiperbola tömörítése vagy nyújtása rendkívül kellemetlen. A matematika oktatónak egyszerűen meg kell tanítania a diákot, hogy ugyanazokat a műszakokat tegye meg.
Ehhez az egész rész elválasztása mellett el kell távolítanunk a nevezőn lévő c együtthatót is.
Az egész rész izolálása frakciókban
Hogyan tanítsuk meg az egész rész kiosztását? Tanítás a matematika nem mindig megfelelő szint felmérése hallgatói tudás és annak ellenére, hogy hiányzik a részletes tanulmány a program tétel a polinom osztás a fennmaradó használt szabály részlege területen. Ha egy tanár felveszi a sarokosztályt, akkor szükség lesz arra, hogy a munkamenetnek csaknem felét töltsék magyarázattal (ha minden bizonnyal pontosan igazolják). Sajnos ez a tanár ideje nem mindig áll rendelkezésre. Jobb, ha egyáltalán nem gondolkodsz semmilyen sarkon.
A hallgató kétféleképpen dolgozik:
1) A tutor megmutatja neki a kész algoritmust a frakcionális függvény néhány példáján.
2) A tanár létrehozza az algoritmus logikai keresésének feltételeit.
Math tanár lapkák üres az üres téglalapok együtthatók (ahogy gyakran használják javára 5-6 osztály), és állítsa be a feladat -, hogy töltse ki a számukat. A kiválasztást balról jobbra kell elvégezni. az első lépésből kiindulva. A diáknak el kell képzelnie, hogyan nyitja meg a konzol. Mivel a közzététele egyetlen Ix-vel rendelkező kifejezést eredményez, éppen ennek a koefficiensnek kell egyenlőnek lennie a legmagasabb koefficienssel a régi, 2x + 3 számlálóban. Ezért nyilvánvaló, hogy az első négyzetben a 2. szám van kitöltve. A matematika oktatójának viszonylag egyszerű törtvonalbeli függvénynek kell lennie, amelyhez c = 1. Csak ezt követően folytathatjuk a példák elemzését egy kellemetlen számlálóval és nevezővel (beleértve a törtek együtthatóit is).
Tovább mennünk. A tanár kinyitja a zárójelet, és az eredményt közvetlenül fölé írja.
A megfelelő pár tényező árnyékolható. A "nyilvánosságra hozott" kifejezéshez szükség van egy ilyen szám hozzáadására a második lépésből, hogy megkapjuk a régi számláló szabad együtthatóját. Nyilvánvaló, hogy ez 7.
Ezután a frakció az egyes frakciók összegére oszlik (általában a felhővel töltött frakciót keressem, összehasonlítva helyüket a pillangó szárnyával). És azt mondom: "Megtörjük a frakciót egy pillangóval." A diákok jól emlékeznek erre a kifejezésre.
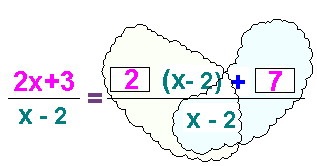
A matematika oktató mutatja az egész folyamatot, hogy az egész részt egy olyan természethez rendelje, amelyre már alkalmazhatja a hiperbola shift algoritmust:
Ha a nevező egynél nagyobb együtthatóval rendelkezik, akkor senki sem hagyhatja ott. Ez az oktatóhoz és a diákhoz további fejfájást okoz a további átalakulás szükségességével kapcsolatban, és a legnehezebb: a tömörítés - nyújtás. A közvetlen arányosság grafikonjának sematikus megépítéséhez a számláló formája nem fontos. A lényeg az, hogy ismerjük a jelét. Akkor jobb, ha áthelyezi a nevező vezető együtthatóját. Például, ha egy függvénygel dolgozunk, egyszerűen csak a zárójelben 3-at veszünk fel, és "felemeljük" a számlálónak, amiben töredék keletkezik. Az építéshez sokkal kényelmesebb kifejezést kapunk: jobbra és 2-re csúcsra tolódik.
Ha van egy "mínusz" a teljes 2 rész és a fennmaradó frakció között, akkor jobb, ha beírjuk a számlálóba. Ellenkező esetben az építmény egy bizonyos szakaszában tovább kell mutatni a hiperbolt az Oy tengelyhez viszonyítva. Ez csak bonyolítja a folyamatot.
A matematika oktatójának aranyszabálya:
a grafikon szimmetriáira, összenyomódásaira vagy szakaszaira vezető összes kényelmetlen együtthatókat át kell vinni a számlálóhoz.
Kolpakov AN Oktató matematika Moszkva. Strogino. A tutorok technikái.