A sugárzás, a lézergyártás és a lézeres üregek erősítésével kapcsolatos feladatok megoldása, 3. oldal
Az aktív közeg optimális hosszúságára feltételezzük, hogy a minimális érték, amelyen az egyenlőség (18) teljesül. Azonban gyakran nem a lézer maximális kimeneti teljesítményének a feltétele, hanem hatékonysága (hatékonysága) alapján, ami azt mutatja, hogy egy külső forrás szivattyú energiafogyasztása mennyire hatékony. Ebben az esetben úgy tekinthető, hogy a maximális hatékonyság akkor érhető el, ha a specifikus teljesítmény maximális értéke eltávolításra kerül az aktív elem hossza egységétől, vagyis a feltétel
A (17) helyét (20) helyettesíti
A numerikus számítások végrehajtása azt mutatja
Az aktív közeg optimális hosszával a kimeneti lézersugárzás intenzitása a (17) képlet alapján számítva:
Ezért nyilvánvaló tény, hogy ebben az esetben a kimeneti sugárzás intenzitásának maximális értéke nem érhető el.
4. A lézer kimeneti tükör reflexiós tényezőjének lehetséges értékeinek meghatározása
Nyilvánvaló, hogy a kimeneti tükör reflexiós tényezőjének minimális értéke nem lehet kisebb, mint az a érték, amelynél a lézer generálás megszakad. Következésképpen azt a küszöbértéket határozza meg, amelyen a generátor öngerjesztése megkezdődik, és amely könnyen megtalálható a (13) állapotból:
Az R maximális értéke lehet egy. Következésképpen a kimeneti tükör reflexiós tényezőjének lehetséges értékei az intervallumban vannak
5. A lézer kimeneti sugárzás intenzitásának optimális értékeinek meghatározása
Az R reflexiós koefficiens függését a (17) képlet határozza meg. Például a MatLab szoftvercsomag használatával és a következő program írásával:
% Az optimális kimeneti intenzitás meghatározása
A lézersugárzás% -a a reflexiós koefficiensből
L = 50; Go = 1,083 * 10 ^ 1; B = 10 ^ (- 4);
n = 1; % utolsó pont
k = -4; fokozat mértéke
A számítások eredményét az 1. ábra mutatja. 4. ábra a függőség grafikonaként.
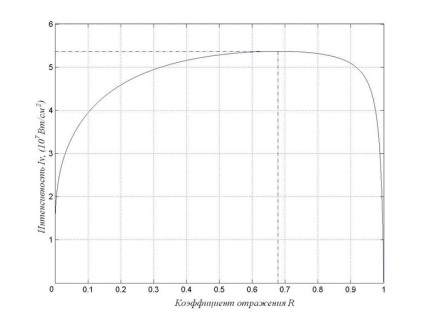
Ábra. 4. A kimeneti lézersugár intenzitásának függvénye a kimeneti tükör reflexiós tényezőjén
Nem nehéz meglátni, hogy a maximális érték elérése megegyezik
6. Következtetések a 2. feladatról
A 2. feladat végrehajtásakor az alábbi eredmények érkeznek:
1. A feladat 1. szakaszában a küszöb feletti felhalmozódás meghatározása: X = 754. Nagyon magas értéke annak köszönhető, hogy a resonátorban a teljes sugárzási veszteség alacsony szintje jelenik meg az amplifikáció szintjéhez képest. Ezt igazolják a lézeres aktív hossz: lp0 = 0,0659 cm küszöbértéke 2a szakaszában, ezért már az l = l hosszúságnál a jel nyereségét összehasonlítjuk a veszteségekkel.
2. A 2b. És a 3. fejezetben bemutatjuk, hogy ha ebben az esetben a kimeneti sugárzás maximális intenzitását kell elérni, akkor ez csak nagyon sok száz métert meghaladó hosszúságú. Ezért ebben az esetben, az 1. opció paramétereinek értékeivel ez lehetetlen. Valójában a gyakorlatban is lehetetlen. Ezért arra kell törekedni, hogy elérjük a kimeneti sugárzás maximális intenzitását, de a lézer maximális hatékonyságának elérését. A 3. fejezet számításai szerint az l = ball = 21,8 cm hosszúságban érhető el, a kimeneti sugárzás intenzitásával. Annak érdekében, hogy a lézer maximális hatékonysággal működjön, az aktív közeg hossza 50 cm-ről l = ball = 21,8 cm-re csökkenthető, ebben az esetben az Iv értékének csökkenése több mint 2-szer csökken.
3. Az 5. ábra azt mutatja, hogy a kimeneti lézersugárzás intenzitásának optimalizálása nem az aktív közeg hossza, hanem a kimeneti tükör reflexiós tényezője szempontjából végezhető el. Ha l = 50 cm, akkor az intenzitás optimális értékét 5,37 × 10 7 W / cm 2 értékkel határozzuk meg, amely a Ropt = 0,68 reflexiós tényező optimális értékénél eléri. Ebben az esetben több érték van meghatározva a (19) és (20) képletekkel.
5. A (17) képletből következik, hogy ha R értéke 0,24-től a 0,68 optimális értékig változik, akkor csak a frakció nevezője fordul elő zárójelben, ami tekinthető R-val arányosnak, mivel az l értékek széles tartományában. Éppen ellenkezőleg, amikor l 50 cm-tõl az optimális értékig = 21,8 cm-re változik, ugyanezen okból csak ennek a frakciónak a számlálója változik. Ezért az I és Y két paraméterrel párhuzamosan történő optimalizálása könnyen megvalósítható, ha R = Ropt és l = pontot állítunk be (17):