Laboratóriumi munkák a fizikán № 5
A tanulmány célja a logaritmikus csillapítás csökkenése és az oszcillációs rendszer csillapítási együtthatójának függése a jelenlegi erősségen.
1. Elméleti rész.
A vibrációs rendszer olyan rendszer, amely oszcillációt végez. Minden oszcilláció szabad, kényszerített, paraméteres és ön-oszcillációra osztható.
A szabad (saját) a rendszer oszcillációinak nevezik, amelyek akkor keletkeznek, amikor a rendszer kezdeti eltérése a stabil egyensúly helyétől független, és nincsenek külső hatások rajta.
Valódi oszcillációs rendszerekben a vibrációs energiát az ellenállók és a belső súrlódási erők ellen használják a munka során, ami a szabad oszcilláció csillapításának oka.
A csillapított oszcillációkat oszcillációnak nevezzük, amelynek amplitúdója idővel csökken.
Alacsony fordulatszámon hagyja, hogy a rezgő erő hatása az oszcilláló rendszeren közvetlenül arányos legyen a sebességgel,
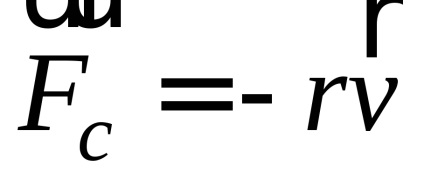
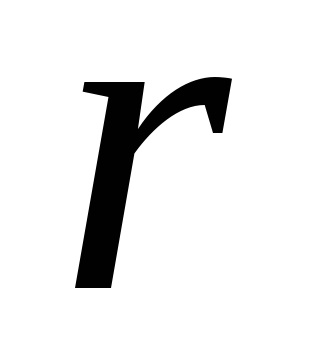
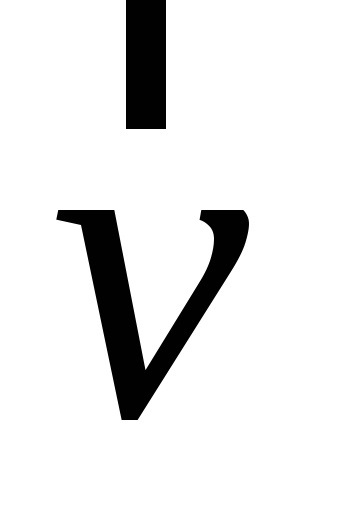
Ezután az oszcillációs rendszer transzlációs mozgásának dinamikai (az OX tengelyre vetített vetület) dinamikájának alapvető egyenlete a következő alakú:
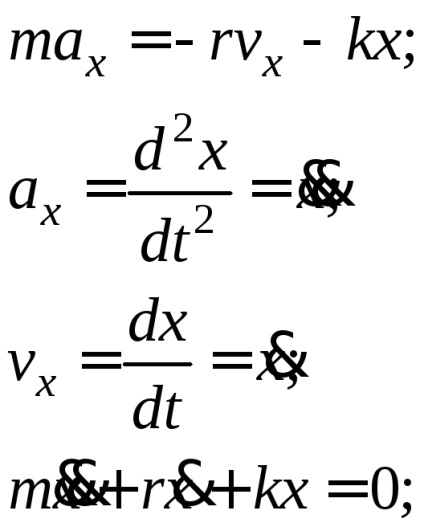
(1) a szabad csillapított oszcillációk differenciál egyenlete, ahol
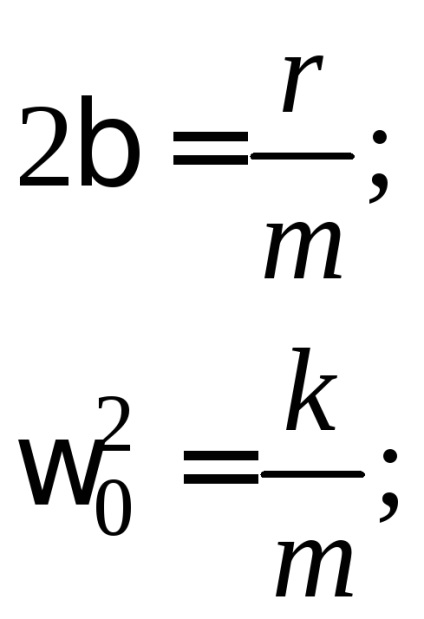
ahol
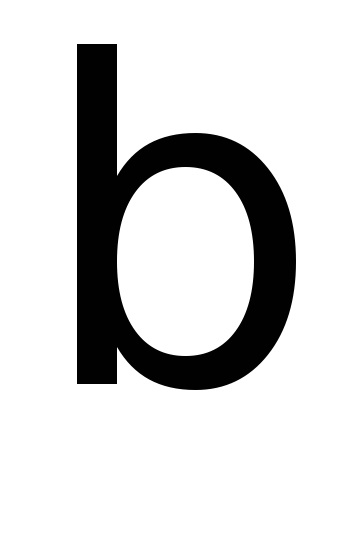
Az (1) differenciálegyenlet megoldása a következő alakú kifejezés:
ahol
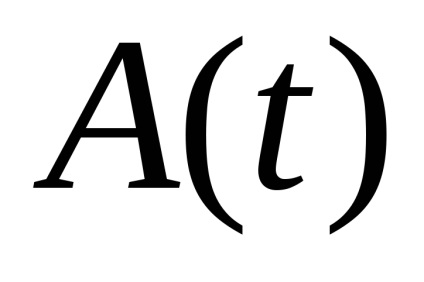
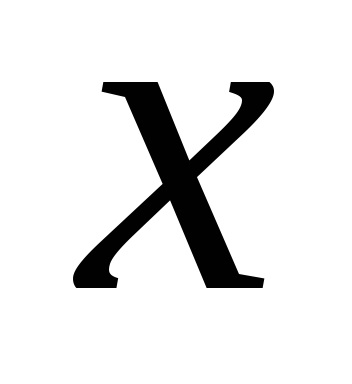
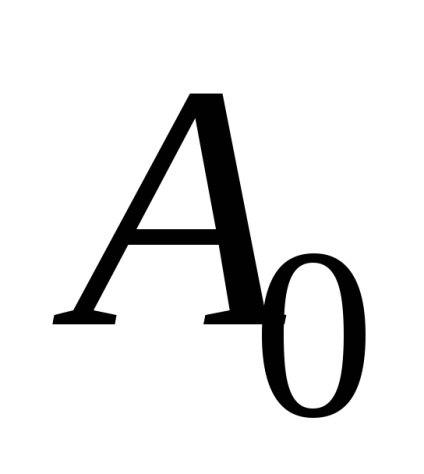
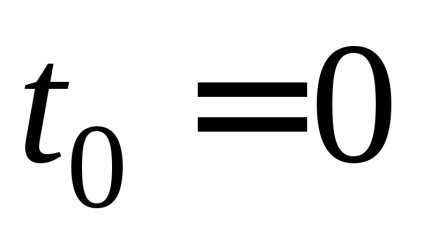
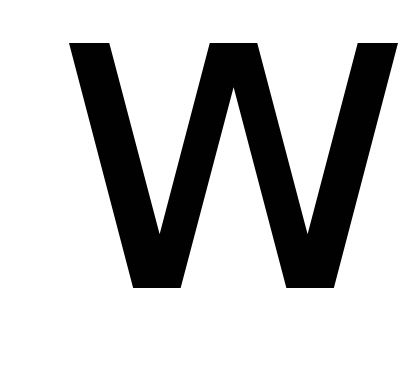
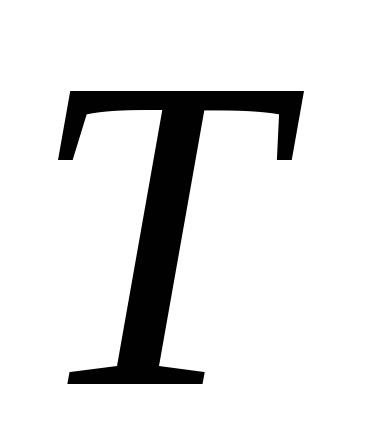
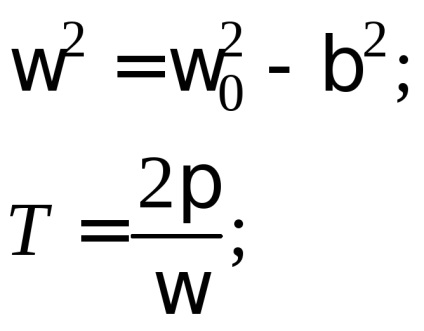
ahol
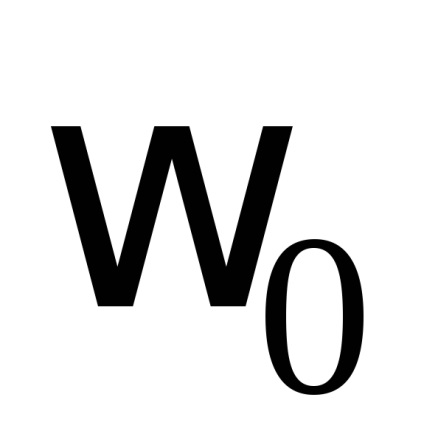
A csillapítási sebesség becsléséhez az oszcilláló rendszer két egymást követő maximális eltérését az egyensúlyi helyzet egyik oldalára lehet használni. Ezt a mennyiséget csillapításnak nevezik
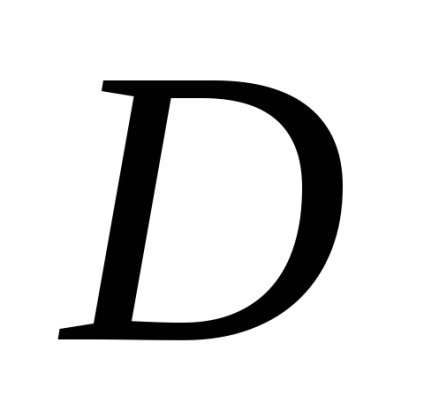
A két egymást követő amplitúdóérték arányának természetes logaritmusa a csillapítás logaritmikus csökkenése
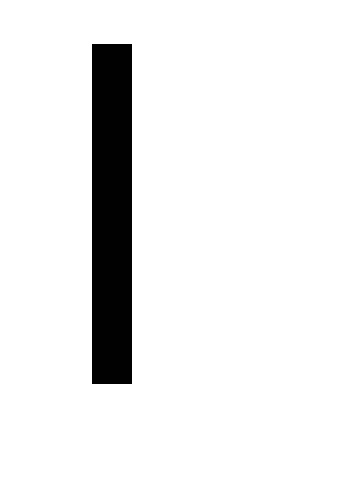
Találjuk meg a logaritmikus csillapítás csökkenés és a csillapítási együttható közötti összefüggést:
2. A kísérleti rész.
Az oszcilláló rendszer egy inga, amelynek alsó terhelése masszív rézlemez (1). Amikor az inga oszcillál, a lemez mágneses térben mozog az "N" és "S" elektromágnes pólusai között (1. ábra).
Az elektromágnes áramkörének hiányában az oszcilláló rendszer lényegtelen ellenállást mutat a felfüggesztés pontjaiban (golyóscsapágyak), így a rezgések nagyon alacsony csillapítással fordulnak elő.
Átadásával áram segítségével tekercsek az elektromágnes mérjük egy ampermérőt (A) felmerülő lemez örvényáramok gátló hatás, így a belső súrlódás oszcilláló rendszerhez, és növeli a csillapítás a rezgések.
A logaritmikus csillapítás csökkenése ezen körülmények között a mágneses mező intenzitásának függvénye az elektromágnes pólusai közötti térben, ezért az áramkör aktuális erősségétől függően változik.
Meg kell jegyezni, hogy a mágneses mező a térben pólusai között az elektromágnes nem homogén, így a logaritmikus dekrementálás függ a kezdeti rezgésamplitúdót. Ezt el lehet kerülni, ha az összes mérést lehetővé ugyanazon a kezdeti amplitúdó a csillapodó rezgéseinek, azaz, az inga oszcilláció elutasíthatja mindig egy és ugyanazon értéket
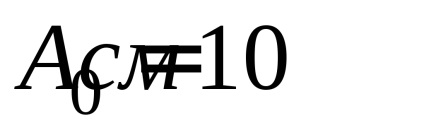
A (3) szerint:
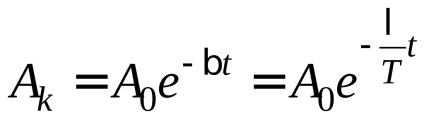
Ezután a kezdeti amplitúdó mérésével
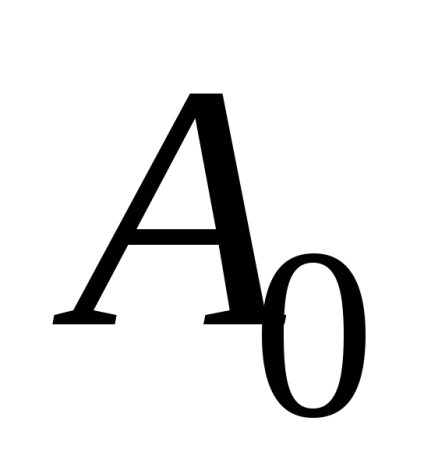
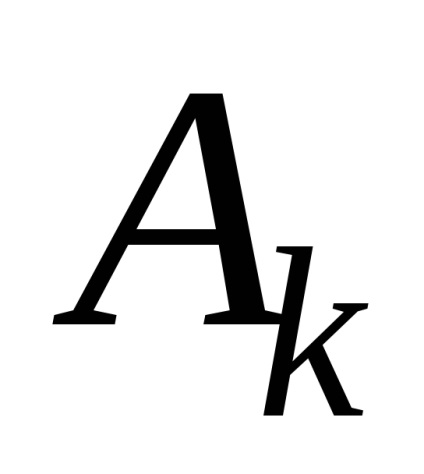
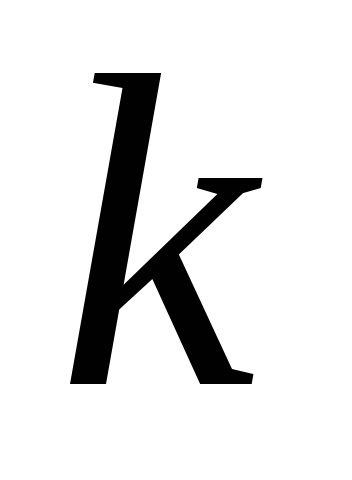

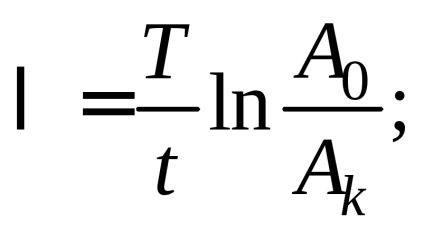
ahol
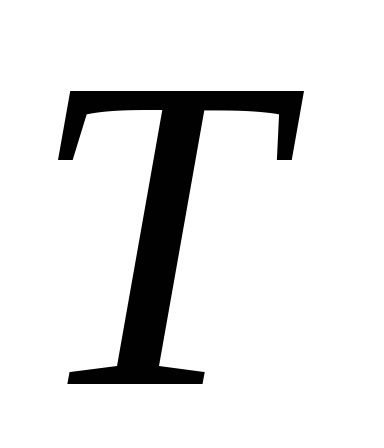
Ez nyilvánvaló
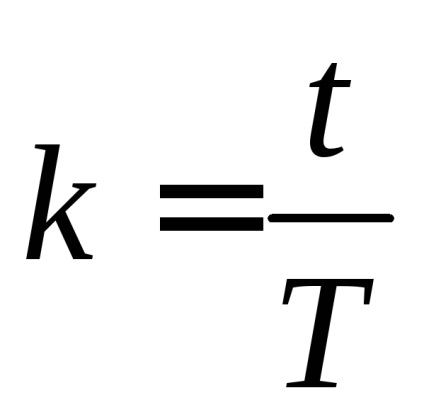
Így annak meghatározása érdekében
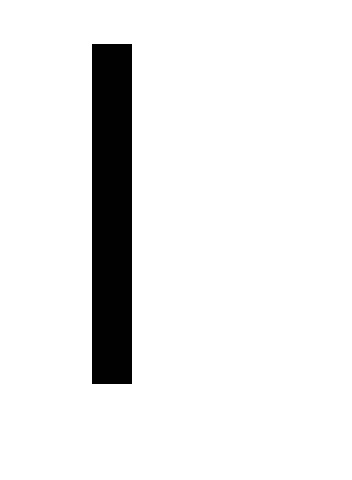
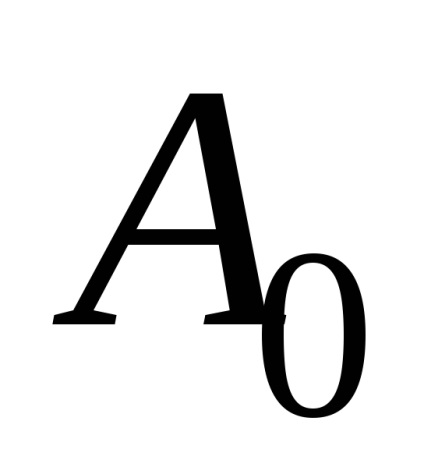
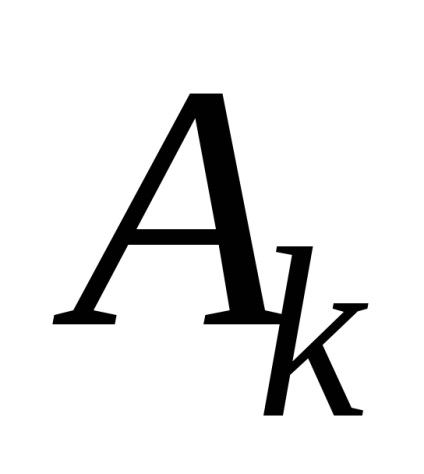
Az amplitúdó mérése egy vonalzóval történik, az inga rézlemezére ragasztva. A megfigyelő szemét oly módon helyezik el, hogy a tekercs mindkét szakasza egyenes vonalon legyen. Az áramot a VS-24M használatával változtatják meg.
Az inga oszcillációs idejének meghatározásához szükséges az idő mérése

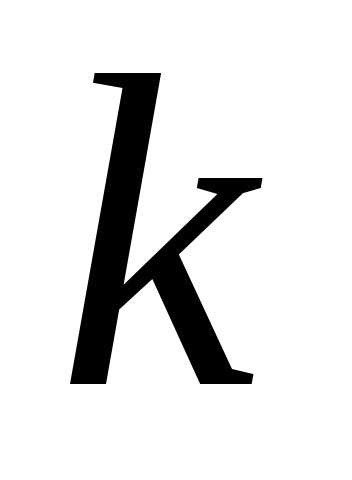
Az inga csillapítási együtthatója a relációból származik:
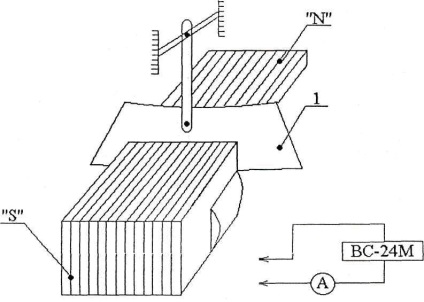
Ábra. 1. Kísérleti rendszer.
1 - rézlemez,
"N", "S" - az elektromágnes pólusai.
3. A kísérlet végrehajtása.
1. Szerelje össze a berendezés mérőkörét (1. ábra). Ebben az esetben a BC-24M áramforrás vezérlő fogantyújának bal szélső helyzetben kell lennie az óramutató járásával ellentétes irányba, amíg meg nem áll.
2. áram hiányában az áramkörben (
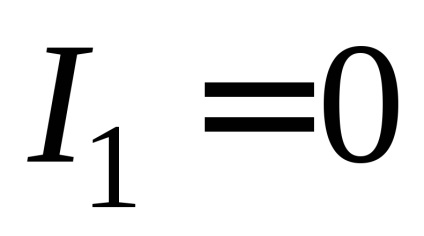
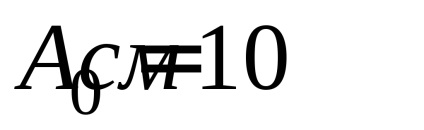
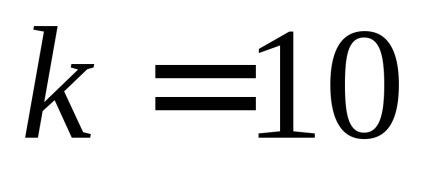

3. A (8), (9), (10) képlet segítségével számítsa ki a logaritmikus csillapítás csökkenést, a csillapított oszcillációs periódust és a csillapítási együtthatót.
4. Ismételje meg a 2. és a 3. tételhez tartozó méréseket és számításokat a következő aktuális értékekhez:
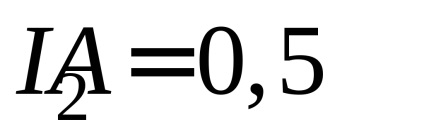
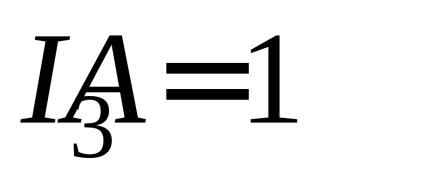
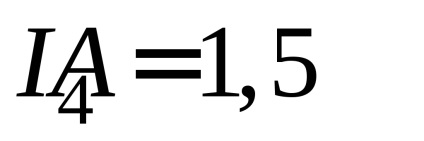
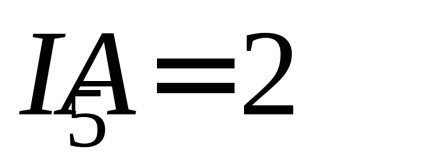
5. Az 1. táblázatban rögzítse a mérések és számítások eredményeit.
6. A mérési eredmények feldolgozása.
Minden egyes számított logaritmikus csökkenési értékre
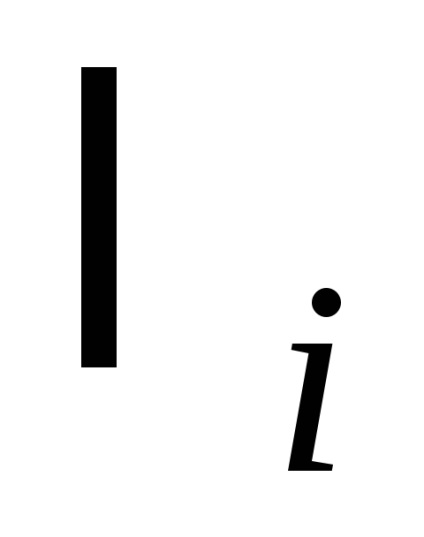
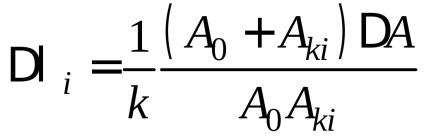
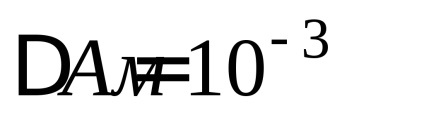
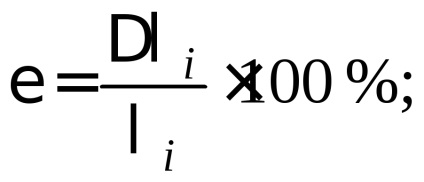
A mérések eredményeit a következőképpen kell írni:
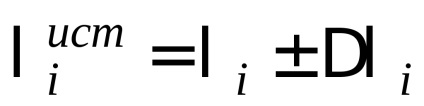
7. Következtetések levonása: hogyan befolyásolja a csillapítás logaritmikus csökkenése és a csillapítási tényező az áram nagyságától.
4. Ellenőrzési kérdések.
1. Írja le a csillapított oszcilláció differenciálegyenletét és megoldását.
2. Írja le a logaritmikus csillapítás csökkentésére és a csillapítási együtthatóra vonatkozó kifejezéseket.
3. A csillapítási inga oszcilláció miatt a kisebb terhelés formájában egy hatalmas rézlemez, oszcilláló pólusai között az elektromágnes egy aktuális a láncban, és anélkül, hogy?
3. N.A. Gladkov. "A" Fizika "kurzus előadásainak anyaga a" Oscillations "témában. Mechanikus hullámok ». M. MSTU, 1987.