Laba-piezoelektromos elem (2018-3)
Reviewer S.S. Nikolaev
Zadorozhny N.A. Chuyev A.S. Sorokina L.A.
Az iránymutatás elméleti részében a közvetlen és az inverz piezoelektromos hatás leírását adjuk meg, a különböző piezo-matériumok jellemzőit és azok alkalmazási területét mutatjuk be. A laboratóriumi beállítás és a kísérlet lefolytatásának leírása megtalálható. A mérési eredmények feldolgozására vonatkozó utasításokat adják meg.
A diákok a 2 éves tanfolyam minden specialitások MSTU. NE Bauman. Ábra. Irodalom. 1 név.
Nikolay Antonovich Zadorozhniy Anatolij Stepanovich Chuev Larisa Alexandrovna Sorokina
A piezoelektromos hatás vizsgálata
Corrector Számítógép elrendezés
A munka célja a piezoelektromos hatás és alkalmazások ismerete;
- piezoelektromos anyagok vizsgálata;
- a kísérlet elvégzésének és az eredmények feldolgozásának készsége.
1756-ban az orosz akadémikus, F. Epinus úgy találta, hogy amikor egy turmalin kristályt melegítettek, az arcán elektromos töltések jelentek meg. Később ezt a jelenséget kapta a piroelektromos hatás neve. F. Epinus feltételezte, hogy a hőmérsékletváltozás során észlelt elektromos jelenségek oka a két felület egyenetlen melegedése, ami mechanikai feszültségek megjelenéséhez vezet a kristályban. Ugyanakkor rámutatott arra is, hogy a pólusok eloszlásának állandósága a kristály egyes végein függ a szerkezetétől és összetételétől, így F. Epinus közeledett a piezoelektromos hatás felfedezéséhez.
A piezoelektromos hatás a kristályok fedezték fel 1880-ban a testvérek és J. P. Curie megfigyelni a felszíni megjelenésével a lemezek kivágott egy bizonyos módon a kvarckristály, elektrosztatikus töltések hatására mechanikai feszültség. Ezek a töltetek arányosak a mechanikai feszültséggel, változtatják a jelet, és eltűnnek a feszültség eltávolításakor.
Az elektrosztatikus töltések kialakulása a dielektrikum felületén és a mechanikai igénybevétel következtében keletkező elektromos polarizáció előfordulása közvetlen piezoelektromos hatásnak nevezik.
A közvetlen piezoelektromos hatás mellett egy inverz piezoelektromos hatás is van. Ez abból a tényből áll, hogy egy piezoelektromos kristálytól bizonyos módon kivágott lemezben mechanikai deformáció következik be az alkalmazott elektromos mező hatása alatt. A mechanikai deformáció értéke pedig arányos az elektromos tér erősségével.
Tekintsük a piezoelektromos elméleti szempontjait.
A piezoelektromos hatás leromlása a deformálható közegben szorosan összefügg a dielektromos polarizáció koncepciójával, amely néhány anyag bizonyos viselkedési jellemzőit tükrözi, különösen a dielektrikumokat elektromos mező hatása alatt.
Az elektrosztatikus mezőben elhelyezett dielektrikum polarizációjának jelensége annak köszönhető, hogy az elektromos töltések jelen vannak a részecskékben és azok egyedi részeiben, amelyek elektromágneses tér hatására elasztikusan eltolhatók. Ellentétben az ingyenes villamos energiával,
egy szigetelő töltés kapcsolódó díjaknak az egyes részek az atomok és molekulák dielektrikumok képesek az anyagi hordozó mozgatható a dielektromos anyag makroszkopikus távolságig, alkotó elektromos dipólusok vagy dipólusok orientálódni mentén rendelkezésre álló mezőbe. Ebben az esetben az atomok vagy molekulák kötődnek a kristályrács teljes vagy elszigetelt részének szerkezetéhez.
Kétféle polarizáció létezik: orientáció és deformáció. Az első a poláris molekulákra vonatkozik, a második a nempoláris molekulákra. A szilárd dielektrikumokban, amelyek kristályrácsjai pozitív és negatív ionokból vannak kialakítva, megfigyelhető az ionpolarizáció.
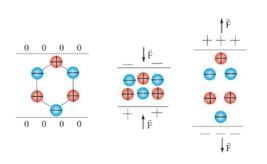
Külső elektromos mező hiányában spontán polarizáció figyelhető meg ilyen dielektrikában; a molekulák teljes elektromos dipólus pillanata eltér a nullától. A ferroelektrics kristályrácsba bejutó ionok mechanikus igénybevételekkel könnyen elmozdíthatók. Egy közvetlen piezoelektromos hatás az elektromos töltések megjelenése bizonyos szimmetriaosztályok kristályainak felületén mechanikai terhelés hatására.
Külső mechanikai igénybevételek hiányában az egységcella elektromos dipólus pillanata nulla (1. Ha ilyen feszültségek hatására a sejtet megnyújtják vagy összenyomják, elektromos dipólus pillanat keletkezik. Ez lesz
,
ahol q az ion töltés, és a a sejt megnyújtása vagy összehúzódása.
A piezoelektromos belsejében lévő elektromos dipólus pillanatainak jelenlétét a piezoelement kristályának vagy elektródáinak ellentétes oldalain megjelenő elektromos töltések jelzik (1.
1. ábra. Piezoelektromos effektus képződése.
A töltés nagysága, amikor a piezoelektromos hatást a reláció határozza meg
ahol: F x - az erő nagysága, amely az i irányba deformálódást okozott; d jk a piezomodul (általános formában, a tenzor).
Kísérletileg bizonyítottuk, hogy a hiányában egy elektromos mező vektort polarizáció a piezoelektromos képviselő térfogatsűrűsége villamos dipólusnyomatékuk társított mechanikai feszültség tenzor lineáris függését képviseli a következő összefüggést:
P i = d ijk σ jk.
P i a P polarizációs vektor komponense az i-i irányban;
σ jk a merőleges irányban keletkező stressztenzens komponense; d ijk - piezoelektromos modulokat három egymásra merőleges irányba.
A teljes polarizációs vektort a
P = P x + P y + P z.
Egyszerűsített formában a polarizáció a következőképpen ábrázolható:
A stressztenzens matematikai kifejezése:
Az új jelölésnél a P polarizációs komponensek kifejezésére kerül sor
P X = d 11 σ 1 + d 12 σ 2 + d 13 σ 3 + d 14 σ 4 + d 15 σ 5 + d 16 σ 6
P Y = d 21 σ 1 + d 22 σ 2 + d 23 σ 3 + d 24 σ 4 + d 25 σ 5 + d 26 σ 6
P Z = d 31 σ 1 + d 32 σ 2 + d 33 σ 3 + d 34 σ 4 + d 35 σ 5 + d 36 σ 6
Így a piezoelektromos hatást egy mátrix írja le 18 piezoelektromos modul részvételével. A kristály fokozódó szimmetriasűrűségével a modulok eltűnése egyre nagyobb lesz.
A közvetlen piezoelektromos hatás megjelenése a Meissner által javasolt modellelemzés segítségével könnyen érthető.
Például a SiO kvarc kémiai képletét. Kristályrácsja pozitív szilícium ionokból és negatív oxigénionokból áll. Ha a kristályt az optikai tengely mentén nézzük, akkor az ionok elrendezése így néz ki:
Az X tengely mentén összenyomva hosszanti piezoelektromos hatást figyelhetünk meg.
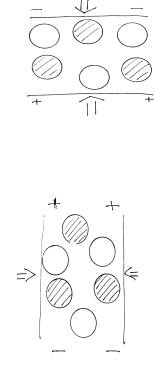
A tömörítés irányának megváltozása a polarizációs töltés jele megváltozásához vezet - egy keresztirányú piezoelektromos hatást figyeltek meg.
A kvarc esetében a piezomodulok a következőkhöz kapcsolódnak:
d 12 = - d 11 d 25 = - d 14 d 26 = - d 11
Mivel minden más modul 0, csak két független modul marad
d 11 = 2,31 10-12 C / H d 14 = 0,7 10-12 C / H
A kvarc piezoelektromos hatását az Eq.
= d 11 σ 1 - d 11 σ 2 + d 14 σ 4
= - d 14 σ 5 - d 11 σ 6
A piezoelektromosság csak akkor jelenik meg, ha a kristály rugalmas deformációjához a kristályegység cellájának pozitív és negatív tölteteinek elhelyezkedési központjainak elmozdulása társul, azaz amikor egy egyedi dipólus pillért indukál, ami szükséges ahhoz, hogy egy dielektrikum elektromos polarizációját mechanikai igénybevétellel kezdjék. A szimmetria-központú struktúrákban a homogén deformáció nem tudja megtörni a kristályrács belső egyensúlyát, ezért a piezoelektromos kristályok csak olyan osztályokból álló kristályok, amelyeknek nincs szimmetria-középpontja. A szimmetria-központ hiánya
Szükséges, de nem elegendő piezoelektromos hatás létezésére, ezért nem minden akcentrikus kristály rendelkezik.
A piezoelektromos hatás nem figyelhető meg szilárd amorf és kriptokristályos dielektrikumokban (szinte izotróp), mivel ez ellentmond a szférikus szimmetriájuknak. Az egyetlen kivétel az, amikor anizotróp hatásúvá válnak a külső erők hatása alatt, és ezáltal részben megszerzik az egykristályok tulajdonságait.
Segnetoele ktri ki (az úgynevezett első anyagot, ahol a ferroelektromos hatást felnyitása -segnetova só) - tvordyedielektriki (nekotoryeionnye ipezoelektriki kristályok), amelynek egy bizonyos hőmérséklet-tartományban elektricheskimdipolnym saját lendület, amely lehet orientálni miatt Alkalmazások vneshnegoelektricheskogo területen. A ferroelektromos anyagok rendelkeznek az elektromos dipólus pillanatnyi hiszterézisével az alkalmazott elektromos tér tekintetében. Ráadásul a ferroelektrics spontán (spontán) polarizáció egy bizonyos hőmérsékleti tartományban, azaz polarizáció és külső elektromos mező hiányában.
Külső elektromos mező hiányában a ferroelektromos olyan, mint a polarizáció különböző irányaival rendelkező domének-régiók mozaikja. A szomszédos tartományokban ezek az irányok eltérőek és egészében a dielektrikum dipólus pillanata nulla. Ha így egy ferroelektromos egy külső elektromos mező csakúgy mint a dipólusmomentumának a domének a területen, és így keletkezett teljes elektromos mezőt domain fenntartása azok egyes orientáció, és megszűnésekor a külső területen. Ezért a ferroelektrics nagyon magas dielektromos permittivitással rendelkezik (például Rochelle só max. ≈ 10 4).
Az anyagok ferroelektromos tulajdonságai nagymértékben függenek a hőmérséklettől. Minden egyes ferroelektrikum esetében van egy bizonyos hőmérséklet, amely fölött szokatlan tulajdonságai eltűnnek, és normál dielektrikumgá válik. Ezt a hőmérsékletet Curie-pontnak hívják (Pierre Curie francia fizikus (1859-1906) tiszteletére). Tipikusan a ferroelektricsnek csak egy Curie pontja van; az egyetlen kivétel a Rochelle-só (-18 és +24 ° C) és az izomorf vegyületek. A Curie pont közelében lévő ferroelektricsen megfigyelhető az anyag specifikus hőjének éles változása is.
Eddig a piezoelektromos hatás nem talál kielégítő kvantitatív leírást a kristályrács modern atomelméletének keretein belül. Még a legegyszerűbb típusú szerkezetek esetében sem lehet közelíteni a piezoelektromos konstansok sorrendjét.
Jelenleg a piezoelektromos hatás fenomenológiai elméletét fejlesztették ki, amely a deformációkat és a mechanikai igénybevételeket mutatja az elektromos térnek és a kristályok polarizációjának. A piezoelektromos kristály hatékonyságát meghatározó paraméterrendszer jön létre. A piezoelektrika fő paraméterei a következők:
A piezoelektromos modul (piezoelektromos modul) dij - meghatározza a kristály (vagy töltéssűrűség) polarizációját egy adott mechanikai terheléshez;
piezoelektromos állandó - meghatározza a kristályban keletkező mechanikai feszültséget egy elektromos mező hatása alatt;
Piezoelektromos állandó g - jellemzi a nyitott áramkörben lévő elektromos feszültséget egy adott mechanikai feszültségnél;
piezoelektromos állandó h - határozza meg a nyitott áramkörben lévő elektromos feszültséget egy adott mechanikai deformációhoz.
Ezek az állandók kapcsolatos mennyiségek és kapcsolódnak egymáshoz a kapcsolatok, amelyek magukban foglalják a rugalmas állandó és dielektromos állandója a kristályok, ezért lehetséges, hogy ezek közül bármelyik. A gyakorlatban a piezomodul a leggyakrabban használt. Piezoelektromos állandók tenzorok, így minden chip lehet több piezoelektromos együtthatók jellemző irányát és nagyságát az alkalmazott deformáció ugyanabban az elektromos töltés.
Minden piezoelektromos egy elektromechanikus energia átalakító, ezért fontos jellemzője az elektromechanikus kapcsolási koefficiens r. Ennek az együtthatónak a négyszöge a mechanikai formában megnyilvánuló energiának az adott típusú deformációhoz viszonyított aránya az áramforrás bemenetén kapott összes villamos energiához viszonyítva.
Sok esetben a gyakorlati alkalmazása piezoelectrics vannak azok jelentős rugalmas tulajdonságokkal, amelyek leírása rugalmassági tényezője - C (Young modulus - E Yu), vagy a reciprok - rugalmassági állandókkal - S.
Amikor a piezoelektromos elemeket rezonátorként használják, egyes esetekben frekvencia-együtthatót vezetnek be. amely a piezoelektromos elem rezonanciafrekvenciája és a geometriai dimenzió eredménye, amely meghatározza az oszcilláció típusát. Ez az érték arányos a hang sebességével a piezoelektromos elem elasztikus hullámainak terjedésével.
Jelenleg számos olyan (több mint 500) anyag ismeretes, amelyek piezoelektromos aktivitást mutatnak. Azonban csak kevesen találnak gyakorlati alkalmazást.
Kvarc. Széles körben rasprostrononny természetben előforduló ásvány, amely alatti hőmérsékleten 573 Celsius fok kristályosodik trigonális trapetsoedricheskom osztály hexagonális rendszerben. Tartozik egy csoportját enantiomer és a természetben előforduló két változatban: balra és jobbra.
A kémiai összetételben a kvarc vízmentes szilícium-dioxid (SiO 2) molekulatömege 60,06 g / mol. A kvarc az egyik legerősebb ásványi anyag, magas kémiai ellenálló képességgel is rendelkezik.
A természetes kvarckristályok külső formái nagyon változatosak. A leggyakoribb forma egy hatszögű prizma és rhombohedra (piramis alakú elemek) kombinációja. A prizma élei a kristály alapjára bomlanak és vízszintes árnyalattal rendelkeznek a felületen.
A piezoelektromos berendezésekben használható kvarc kristályok, töredékek és pelletek formájában található. A kvarckristályok színe színtelen-átlátszó (kőzet kristály) és fekete (morion).
Jelenleg, az autoklávban növekvő hőmérsékleten és nyomással készült, természetes alkáli-telített alkalikus oldatokkal termesztett természetes szintetikus kvarckristályokat használnak.
A kvarc piezoelektromos tulajdonságait széles körben használják a rádiófrekvenciák stabilizálásához és szűréséhez, ultrahang rezgések generálásához és mechanikai mennyiségek méréséhez (piezometria).
Turmalin. A turmalin kristályosodik a trigonális rendszer trigonális-piramisális osztályában. Prizmás kristályok hosszanti árnyékolással, hosszúkás, gyakran tű alakúak.
A kémiai összetétel szerint a turmalin egy komplex alumínium-bór-szilikát, magnézium-, vas- vagy alkálifém-szennyeződésekkel (Na, Li, K).
A szín fekete-zöld, piros is, egyetlen, kevésbé színtelen. A súrlódás villamosítása esetén erős piroelektromos hatása van.
A turmalin széles körben elterjedt a természetben, de a legtöbb esetben a kristályok repedésekkel vannak tele. Ritka a piezoelektromos rezonátorokra alkalmas, hibamentes kristályok.
Lime só. A vas só kristályosodik a rhombikus syngony rhombotetrahedral osztályában. Az enantiomorf osztályhoz való tartozás meghatározza a Rochelle só jobb és bal kristályainak létezésének elméleti lehetőségét. Azonban a Rochelle só kristályai, amelyek borkészítési hulladékból származnak, csak igaz.