A síkgörbék ívének számát, az ingyenes kurzusdokumentumokat, absztraktokat és disszertációkat
Az elemi geometriában mértük az egyenes vonalú szegmensek hosszát, valamint a kör és annak részei hosszát. A kör hosszára a körben beírt rendszeres sokszögek kerületének határát elfogadják, korlátlan számú oldaluk számának növelésével. Ezt a koncepciót minden görbére általánosságban szoktuk.
Definíció. DlinoyL AB ív a határ felé, amely a kerülete a beírt sokszög ebben ív, ha a szám a jegyei, korlátozás nélkül, a maximális hosszát a linkeket nullára:
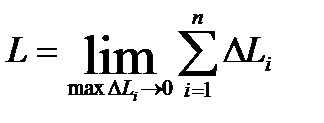
Azokat a görbéket, amelyekre ez a határérték létezik, úgy nevezik, hogy helyrehozható.
Tétel. Adjuk meg az AB görbét az y = f (x) egyenlet alapján, ahol f (x) egy folytonos függvény, amelynek folytonos származéka van a szegmens minden pontján [a, b]. Ezután az AB ív hossza:
/>
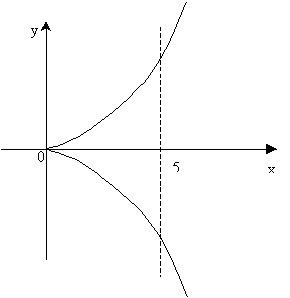
Példa 1. Keresse meg a félkamrás parabola ívhosszát x = 0 és x = 5 között. Megoldás: A görbe szimmetrikus az Ox tengely körül. Találjuk meg a görbe felső ágának hosszát. A talált egyenletből
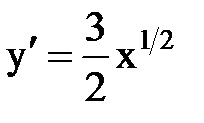
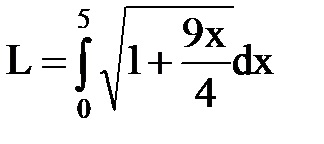
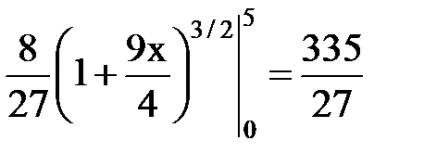
A parabola ívének hosszának megkereséséhez az alábbi képleteket használhatjuk: Azóta az (1) képlet segítségével kapjuk meg a következőket:
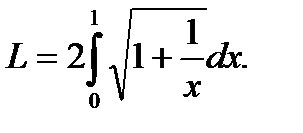
Ebből a célból az x parabola egyenletből és a származtatottnak a "játék" -hoz viszonyított kifejezéséből adódik:
Ezután az ív hossza egyenlő lesz: