Milyen gyorsan mozog a szöcske árnyéka (2018. november 26.)
Tetszett a feladat, mert egyszerű, de nem jól viselt (nem találkoztam hasonló).
A megoldási terv a következő:
Ha azonnal megjelenik. Regisztrálatlan felhasználók számára a gyorsítótárazást 1 óráig használják, a regisztrált felhasználók számára pedig automatikusan letiltásra kerül. De van még gyorsítótár a böngésző oldalán.
Nagyon köszönöm! Győződjön meg róla, hogy kirakja a megoldást. -)
2) Ha T kisebb, mint az ugrás ideje (ami valószínűleg hallható), akkor a legkönnyebb ezt eldönteni:
különben a kérdésnek nincs értelme.
4) Mozgás kinematikai egyenleteket írjon fel ezekre a tengelyekre (ne felejtsd el a g vetületeket, hogy nem nulla),
nem világos, hogy miért kell a mozgás kinematikai egyenleteit összeállítani, ha a sebességet a vízszintes és a függőleges sebesség komponensek összekapcsolásával választjuk meg a nap kiválasztott SC-jén.
5) A kinematikai egyenletből keresse meg a T pontban a vetületben a sebességet a tengelyre merőleges irányban a nap irányába,
nem lesz ez a sebesség függőleges összetevője?
2) rendelkezik. Ezután a sebesség 0. A teljes megoldásnak meg kell határoznia a sebességet a T. függvényében. Ha T kisebb, mint a repülési idő, és a sebesség 0, ha még több.
4) a sebesség egy egyenletét értjük.
5) Ez lesz a sebesség függőleges összetevője?
Ha a tengely a Nap OY-ban van. Az OX merőleges. akkor ez lesz az OX tengelyre vetített vetítés. Mivel az OX tengely nem függőleges, nem lesz függőleges összetevő.
És újra: a hiba megoldása során: írtam nem 1 / cos φ. de 1 / sin φ.
Adjuk meg a koordináta változásának egyenletét az X tengely mentén.
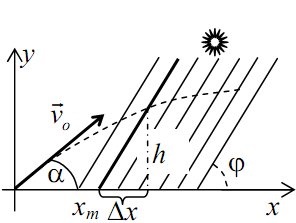
Az árnyék vége koordinátáját a következő kifejezés határozza meg:
xm = x - δx = vo t cos α - h / tan φ.
ahol h a szöcske emelkedése magassága t időpontban.
h = vo t sin α-gt 2/2.
A változás az egyenletben az árnyék koordinátáit:
xm = (vo cos a - vo sin α / tan φ) × t + 2 / (2tg φ).
Az idő koordinátájának egyenletét differenciálva megtaláljuk a szöcskék árnyékának sebességét az idő múlásával: