Határolt függő változókkal rendelkező modellek
Előfordulásakor, ha az adatok közül a nagyobb mennyiségű adatok egy részét (megfigyelések), például a tanulmány tekinthető jövedelmű családok alatti jövedelemmel vagy egy bizonyos szint felett (például a szegénységi küszöb).
A minták csonkítása helyett a cenzúrázás is használható. Különösen a teljes mintát veszik figyelembe jövedelemkutatásban, de feltételezzük, hogy a jövedelemtulajdonosok egy bizonyos jövedelmi szint felett vagy alatt ugyanolyan szinten vannak. A minták cenzúrázásának és csonkításának következménye az eloszlások mintaparamétereinek, különösen matematikai elvárásainak és eltéréseinek a torzítása. Ennek megfelelően a csonka és a cenzúrázott minták alapján kapott következtetéseket nagyon körültekintően kell átadni az általános lakosságnak.
A csonkolt minták modelljei
Tegyük fel, hogy a csonkított eloszlás része egy korlátlan eloszlásnak, amely egy bizonyos küszöb felett vagy alatt van.
Egy folyamatos, véletlen változó sűrűsége z. a b szint fölött csonka. a következő kifejezés szerint határozzák meg:
A kifejezés (10.136) a feltételes valószínűségi képletből következik. Valójában annak a feltételes valószínűsége, hogy egy véletlen változó z bizonyos értéket vesz igénybe azzal a feltétellel, hogy z ò ò /ò A kifejezés bal és jobb oldali oldalainak (10.137) differenciálása z-re vonatkoztatva. kapunk (10.136). Számos gyakorlati tanulmányban azt feltételezzük, hogy a z valószínűségi változót a szokásos törvény szerint osztjuk szét. Ebben az esetben annak valószínűsége, hogy z> b-t a következő kifejezéssel határozzuk meg: ahol m és s a z valószínűségi változó várakozása és szórása; b = (b-m) / s; Φ (.) A normál normál integrált eloszlás értéke a megfelelő ponton. Ezután a (10.136) kifejezés szerint a csonkított normál eloszlás sűrűségfüggvénye a következő: ahol j (.) a szokásos normál eloszlásfüggvény. Az 1. ábrán. 10.6. Ábra egy csonkolt normál normál eloszlás sűrűségének grafikonja m = 0 és s = 1 esetén b = -0,5; 0; 0.5. A grafikonok azt ezen ábra mutatja azt mutatja, hogy a csonkolás az egyfajta „emeli” a függvényt a fennmaradó után csonkolás fölötti területen a grafikont a funkció „nem-csonka” eloszlás. Az alábbiakban egy csonkolt eloszlású véletlen változót nevezünk csonkolt véletlen változónak. Megjegyezzük, hogy a csonkított véletlen változó matematikai elvárásait és varianciáját a következő kifejezések alapján határozzuk meg: M [z | z> b] =ò D [z | z> b] =ò Elvégzése az integráció a (10,140) - (10,141), tekintettel arra a tényre, hogy a sűrűsége f (. Z z> b) által meghatározott expressziós (10,139), azt találjuk, hogy a várható értéke és szórása a csonka valószínűségi változó z, rendre: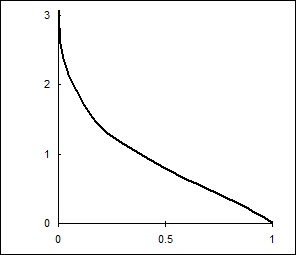
Ris.10.8. A feltételes átlag a csonkítás mértékének függvényében.
Tegyük fel, hogy egy véletlen változó yt. Függése. az őt befolyásoló tényezők értékeiből az alábbiak szerint reprezentálható:
ahol xt a független változók vektora, amelyek befolyásolják a yt változót; a a paraméterek vektora; et a modell hibája, amelyre feltételezzük, hogy azt a normál normális törvény szerint osztják szét nulla matematikai várakozással és állandó varianciával, és
A yt változó. amelyet a (10.148) kifejezés ír le, a normális törvény szerint osztják szét matematikai elvárással mt = a ¢ s xt és variancia s 2.
Tekintsük az yt függő változó eloszlását, feltéve, hogy az yt észlelt értéke meghalad egy bizonyos küszöböt b. A (10.142) kifejezés alapján azt kapjuk, hogy a feltételes matematikai várakozás yt modell (10.148) egy xt és a nemlineáris függvénye. és meghatározása szerint
M [yt | yt> b] = a ¢ s xt +
A (10.149) kifejezést az l (bt) hibák függvényében újraszövegezzük (lásd a (10.144) kifejezést):
Figyelembe véve a kifejezés formáját (10.150), becsüljük az xt faktorok marginális hatásának nagyságát csonkolt minta esetén:
Mivel az xt tényezők mindegyikére a 0 reláció Megjegyezzük, hogy mivel a specificitása expressziós (10.150) et hibamodell (10,146), épített a csonkított minta, ez a várakozás s × l (bt). Ebben az esetben az err hiba varianciája a következőképpen határozható meg: Így, a kifejezések (10.150) és (10,152), hogy a becslések a modell paramétereinek (10,148), alapján meghatározott, a csonkított minta függő változó (yt> b vagy yt