A csomópontok legnagyobb közös osztója
Bármely természetes szám mindig osztható 1 és önmagában. A 2-es szám a legkisebb prímszám. Ez az egyetlen prímszám, a fennmaradó prímszámok furcsaak.
Sok prímszám van, és az első közülük a 2. szám. Mindazonáltal nincs első prímszám.
De sok természetes szám egyenletesen oszlik más természetes számokra.
- a 12 szám 1, 2, 3, 4, 6, 12;
- a 36. szám 1, 2, 3, 4, 6, 12, 18, 36-ra van osztva.
A számokat, amelyekre a szám teljes egészében van felosztva (12: 1, 2, 3, 4, 6 és 12) hívják egy szám osztóinak. A természetes számosztó a természetes szám, amely egy adott számot oszt meg anélkül, hogy fennmaradna. Egy természetes szám, amelynek több mint két osztója van, összetettnek nevezzük. Ne feledje, hogy a 12-es és 36-as számok közös osztókkal rendelkeznek. Ezek a számok: 1, 2, 3, 4, 6, 12. A számok legnagyobb osztóinak száma 12.
Az a és b számú két szám közös osztója az a szám, amellyel mind az a, mind a b értékek maradék nélkül oszthatók. A több szám közös osztója (GCD) egy szám, amely mindegyikhez osztóként szolgál.
Röviden, az a és b legnagyobb közös osztója:
Egy példa. Isten (12, 36) = 12.
A megoldási rekordban lévő számok osztóit nagy "D" jelöli.
A 7. és 9. számok csak egy közös osztószámot tartalmaznak. Az ilyen számokat egymással kölcsönösen egyszerű slimesnek hívják.
A kölcsönös prímszámok olyan természetes számok, amelyeknek csak egy közös osztója van. A GCD értéke 1.
A legnagyobb közös osztó (GCD) tulajdonságai.
- A fő tulajdonság: az m és n legnagyobb közös osztó osztható bármelyik közös osztóval. Egy példa. a 12. és 18. számnál a legnagyobb közös osztó 6; ez a számok összes osztójára oszlik: 1, 2, 3, 6.
- 1. Következtetés: az m és n közös osztók halmaza egybeesik a GCD osztóegységével (m. N).
- 2. összefüggés: a közös többszörös m és n halmaza egybeesik a többszörös LCM-k (m. N) halmazával.
- Ha m osztható n-vel. akkor a GCD (m. n) = n. Különösen a GCD (n.) = N.
- - a közös tényező GCD-jelként tekinthető.
- Ha ezután a számok szerinti megosztás után kölcsönösen egyszerűvé válik, vagyis.
Ez többek között azt jelenti, hogy ahhoz, hogy a lövés, hogy nem csökkenthető jelenti azt, hogy kell osztani a számláló és a nevező által GCD.
- Sokszorozódás: ha kölcsönösen egyszerű, akkor:
- Az m és n számok legnagyobb közös osztóját a lineáris kombinációk halmazának legkisebb pozitív elemeként definiálhatjuk:
és ezért az m és n számok lineáris kombinációjával reprezentáljuk:
.
Ezt a kapcsolatot Bezout-kapcsolatnak nevezik. és az u és v együtthatók a Bezout-együtthatók. A Bezout-együtthatókat hatékonyan kiszámítja a kiterjesztett euklideszi algoritmus. Ez az állítás általánosítható készlet a természetes számok - a jelentése, hogy az alcsoport által generált, - ciklikus és generálja egy elem: GCD (a1 a2 ... an ...).
A legnagyobb közös osztó (GCD) kiszámítása.
A két szám GCD számításának hatékony módszerei az Euklideszi algoritmus és a bináris algoritmus. Ezenkívül a GCD érték (m, n) könnyen kiszámítható, ha az m és n kanonikus dekompozíciója egyszerű tényezőkre ismert:
ahol különböző prímszámok, és u nemnegatív egész számok (lehetnek nullák, ha a megfelelő primer hiányzik a bővítésben). Ezután a GCD (m, n) és az LCM (m, n) a következő képletekkel fejezhető ki:
Ha több mint két szám van: a GCD-t a következő algoritmus találja meg:
- ez a szükséges GCD.
Is, hogy megtalálja a legnagyobb közös osztót. az egyes számokat az elsődleges tényezőkkel bővíthetjük. Ezután külön írja le azokat a tényezőket, amelyek az összes megadott számot beírják. Ezután szaporítjuk egymás között a számokat - a szorzás eredménye és a legnagyobb közös osztó.
Elemezzük lépésről lépésre a legnagyobb közös osztó kiszámítását:
1. Bővítse a számosztók elsődleges tényezőként:
A számításokat kényelmesen rögzíthetjük egy függőleges sáv segítségével. A vonal bal oldalán először írja be az osztalékot, a jobb oldalon - a megosztót. Továbbá a bal oszlopban a hányadosok értékeit jegyezzük meg. Mutassuk meg egyszerre egy példát. A 28-as és a 64-es számokat elsõdleges tényezõvé teszik.
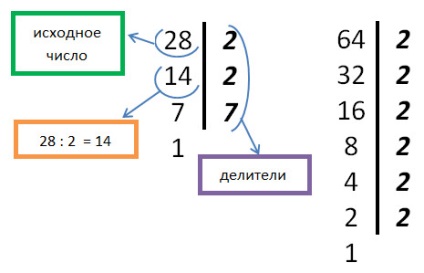
2. Ugyanazokat az egyszerű tényezőket hangsúlyozzuk mindkét számban:
28 = 2 • 2 • 7
64 = 2 • 2 • 2 • 2 • 2 • 2
3. Keresse meg ugyanazokat az egyszerű tényezőket, és írja le a választ:
GCD (28; 64) = 2 • 2 = 4
A válasz: GCD (28; 64) = 4
A GCD helyét kétféle módon találhatja meg: egy oszlopban (mint fent) vagy "sorban".
A GCD írásának első módja:
Keresse meg a 48 és 36 GCD-ket.
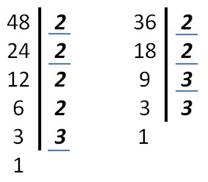
GCD (48; 36) = 2 • 2 • 3 = 12
A második módja a GCD írásnak:
Most leírjuk a GCD keresés megoldását a sorban. Keresse meg a GCD 10-et és a 15-öt.