20. fejezet nyírási (nyíró) 20L
A nyírás egyfajta deformáció, amelyben csak a keresztnyaláb keresztmetszetében keletkezik keresztirányú erő. Az eltolódás deformációja megfigyelhető például fém ollók vagy rudak olló ollóval (20.1. Ábra, a).
Vegyünk egy A keresztmetszetű sávot, amely merőleges a tengelyre, amelyre két egyenlő és ellentétes irányú F erő alkalmazható; A cselekvési irányok párhuzamosak és
viszonylag kis távolságra vannak egymástól. A keresztirányú Q erő meghatározásához a keresztmetszeti módszert alkalmazzuk (20.1, b ábra).
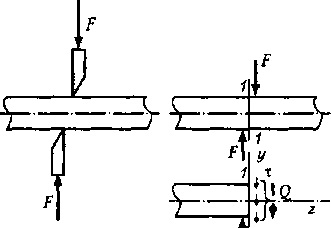
A keresztmetszet minden pontján elosztott erők hatnak, amelynek eredményét a gerenda bal oldalának egyensúlyi állapota határozza meg;
ahonnan meghatározzuk a keresztirányú erőt
A keresztirányú erő a nyíróvonal keresztirányú szakaszában lévő belső tangenciális erők eredménye.
Természetesen azt feltételezzük, hogy a rúd keresztmetszetében csak nyírófeszültségek hatnak a nyíróerőre, feltételezzük, hogy ezek a feszültségek egyenletesen oszlanak el a keresztmetszeten, és ennek következtében meghatározhatók
Nyilvánvaló, hogy a keresztmetszet alakja nem befolyásolja a nyírási feszültség értékét.
Megjegyzés. Az ebben sub számítás nyírófeszültségek nyíró hozzávetőleges, mert kényszeríti a vonal cselekvési FIQ (lásd. Ábra. 20.1, B) nem irányul egy egyenes vonal, és szigorúan véve, ezek a B-ly nem kiegyensúlyozott rendszert, és képviselik egy pár erők . Azonban ennek a párnak (a kis vállnak köszönhetően) a pillanata kicsi, és az ennek megfelelő feszültségek elhanyagolhatók.
A nyírószilárdság számítása
A szerkezeti rész szilárdságának feltétele, hogy a benne lévő maximális feszültség (működési feszültség) ne haladja meg a megengedett értéket.
Becsült képlet a nyíráshoz
a következőképpen olvasható: a% = Q / A képlet által kiszámított tangenciális nyírófeszültség nem haladhatja meg a megengedett feszültséget.
A tervezési képlet szerint elvégzik a tervezési és vizsgálati számításokat, és meghatározzák a megengedett terhelést.
Az anyag megsemmisítéséhez hozzárendelt nyírási deformációkat fémdarabokra való hivatkozással vagy nyírással (nem fémes szerkezetekre utalva) neveznek.
A megengedhető nyírófeszültség a kitermelési ponttól függően szálkás anyagokra van kiválasztva. A gépiparban csapokhoz, csavarokhoz, tüskékhez stb. vesz
A fa esetében a vágás megengedett nyírási feszültsége 0,5 és 1,4 MPa között változik, és függ a fa típusától és a vágás irányától a rostok irányához képest.
A szelet kiszámításánál, ha a csatlakozást több azonos alkatrész (csavar, szegecs stb.) Teszi ki, feltételezzük, hogy mindegyikük egyenletesen van betöltve.
A nyírócsatlakozások számításánál rendszerint ellenőrizni kell ezeknek a csatlakozásoknak a szilárdságát a zúzáshoz.
20.1 példa. Határozza meg a szükséges F erő értékét, hogy az a = 25 mm méretű négyzet alakú nyílást az 5 mm vastagságú acélszalagban érje el, ha a nyírószilárdság végső szilárdsága 360 MPa. Határozza meg a préselési feszültségeket a lyukasztásnál (20.2. Ábra).
A megoldás. Határozza meg az F destruktív terhelést:
Az Asp nyírási területe megegyezik a lyukasztott lyuk oldalfelületének területével:
Ap = 4 * 25 * KG 3 • 10 • 10 '3 = 1000 10 "* m 2. Következésképpen F a D = 360-10 6 -1000 10 -6 = 360 10 3 N tartományban lévő mennyiség.
Határozza meg a préselési feszültségeket a lyukasztásban:
ahol A a lyuk keresztmetszete;
A = n 2 = 25 2 -10 -6 = 625-10 -6 m 2,
<ус = F/A= 360-10 3 / (625 ■ 10 -6 ) = 576 1 0 6 Па = 576 МПа.
20.2. Példa. Határozzuk meg a feszítéseket és a nyírást a rúd fején, az F = 100 kN erővel meghúzva. Tekintettel: D = 32 mm, d = 20 mm, h = 12 mm (20.3 ábra).
A megoldás. Határozza meg az LSN1 összetapadási területét és az Asp-fej nyíró területét. A fej csapágyfelületének területe, amely a zúzással dolgozik, a következő:
A vágási terület egyenlő a henger oldalfelületének a d átmérővel és a h \
Határozza meg a fej feszülését és nyírását:
20.3. Példa. A 19.6. Példa szerinti körülmények között határozza meg a csavarban lévő nyírófeszültségeket (lásd a 19.14. Ábrát).
A megoldás. A csavarban lévő nyírási feszültségeket az m = F / Ap képlet határozza meg. A levágási terület a két szegmens keresztmetszetét jelenti:
Asp = 2. 2/4 = nd 2/2,
Deformáció és Hooke törvénye a nyírás alatt
Annak megállapítására, a jellemző paraméterek a nyírási alakváltozás, tekintsünk egy gerenda elem formájában egy paralelepipedon Abed, a szélén, amely a fellépés-nyírófeszültségek léteznek csak az x és protivopo hamis kötött képviselnek parallelepipedon schemlennoy mereven (ábra. 20.4). A nyírási alakváltozás ebben az elemben úgy van kialakítva, hogy a parallelepipedés derékszögét csavarja az arc bc transzlációs elmozdulása következtében a szakaszhoz viszonyítva, feltételezve rögzítve. A eltolódás deformációját az y szöge határozza meg, és nyírási szögnek nevezik, vagy o m - nyírással (mivel ez a paraméter
nem függ a h távolságtól, amelynél a váltás történik). Az a nagyságú bbv, amelyen a mozgatható felület a nem mozgatható felülethez képest mozog, abszolút eltolásnak nevezik. A relatív y eltolódást radianban fejezzük ki.
A nyíróerő alatt húzódó stresszek és deformációk összefüggésben vannak egymással a függőséggel, amit Hooke nyírási törvénynek neveznek.
Hooke törvénye a váltás alatt csak bizonyos terhelési határértékeken érvényes, és a következőképpen van megfogalmazva: a tangenciális stressz közvetlenül arányos a relatív elmozdulással.
Matematikailag Hooke törvényét egyenlőség formájában lehet megírni
Az arányossági tényező G jellemzi az anyag merevségét (vagyis az ellenállóképességét az elasztikus alakváltozások ellen) a nyírás alatt, és a második fajta nyírási modulusának vagy elasztikus modulusának nevezik.
A rugalmas modulus és a feszültség ugyanabban az egységben fejeződik ki:
G, MPa értékeit adjuk meg néhány anyag esetében:
Sárgaréz (3,5, 3,7) -10 4
Alumínium (2,6 2,7 V 10 4
Következtetésként megjegyezzük, hogy az E, G és v elasztikus konstansok között a következő kapcsolat áll fenn:
A v = 0,25-ös acélok esetében kapjuk
A nyírási törvény hangsúlyozza
A tangenciális feszültségek törvénye a következőképpen van megfogalmazva: tangenciális feszültségek két egymásra merőleges, közös élükre merőleges felületen abszolút értékben egyenlők.
A test belsejében egy bizonyos pont közelében levágunk egy elemi párhuzamos tengely méretét dr, dy, dz (20.5, a ábra).
Engedje meg, hogy a tangenciális feszültség m ezen parallelepiped felső felületére hatjon, és az ebben az arcban ható erő egyenlő
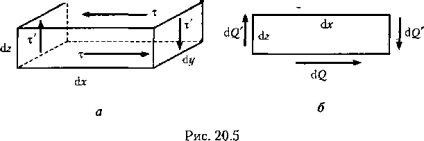
Mivel a parallelepipedus a test belsejében egyensúlyban van, akkor - O, ezért a parallelepiped alsó oldalán
ugyanazzal az erővel dQ, de az ellenkező irányba. Egy pár erő (dQ, dQ) hajlamos elfordítani az irányt ellentétes irányba (20.5. Ábra, b).
Mivel a parallelepipedus egyensúlyban van, akkor = 0,
következésképpen a két erőt (dQ, dQ) kiegyenlítjük egy másik párral egy pillanattal, amely egyenlő az első pár pillanatával. Természetesen azt feltételezzük, hogy a második párt a parallelepipedus oldala (jobb és bal oldali) érintőfeszültségei alkotják dQ '= χ' dydz. ezért
xdxdydz - t 'dxdydz,
Felhívjuk a figyelmet arra a tényre, hogy a két egymásra merőleges keresztmetszetű páros tangenciális feszültség a szakaszok síkjainak metszésvonalához vagy ebből a vonalból áll.
Feszültség alatt álló szakaszokban hangsúlyozza.
A deformált test minden pontján végtelen számú, különböző módon orientált szekcionált repülőgépet lehet rajzolni.
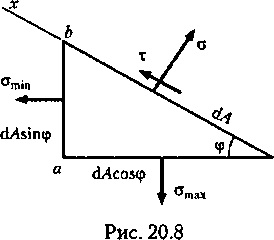
Tekintsünk egy állandó A keresztmetszet egyenes nyalábját, amelyet F erővel terítünk (20.6. Ábra, a). Vágja a gerendát az 1-1 síkkal, haladjon át a B ponton, és szögben keresztmetszetű legyen <р, отбросим верхнюю часть и рассмотрим равновесие нижней.
Nyilvánvaló, hogy a létrejövő N belső erő egy ferde szakaszban megegyezik az F feszítőerővel:
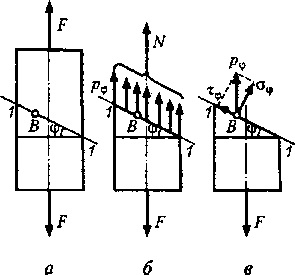
és a pf feszültségek párhuzamosak a gerenda tengelyével (20.6.6 ábra). Feltéve, hogy a pv feszültség egyenletesen oszlik el a ferde keresztmetszet felett, akkor megkapjuk
ahol A a ferde részszakasz területe.
A keresztmetszeti normál feszültségek egyenlők
A p teljes feszültséget a ferde szakasz pontjánál a normál cf és a Tf érintőfeszültség (20.6, c ábra) bontjuk; majd
= pφ costp = acos 2 ф;
= ru sincp = stsoff etf - (o / 2) 5t2f.
A következtetés az, hogy a húzó rúd keresztmetszete ferde-Niyah előfordulnak egyenletesen elosztott merőleges keresztmetszetben kiterjedő és a nyírófeszültség és a megfelelő ezeknek feszültség-zheniyam húzó és nyíró deformációt.
Tekintsünk különleges eseteket:
A normál feszültségeknek a keresztmetszetben maximális értéke van:
A keresztmetszet tangenciális feszültsége nulla;
A tangenciális feszültségek 45 ° -os szögben érik el a tengelyre hajló szelvényeket. Ezek a feszültségek az oka a lejtős Luders-Chernov-vonal kialakulásának egy szakaszon, amikor az olvadékfolyási határértéket elérik;
A gerenda hosszirányú szakaszain nincs érintő vagy normál feszültség (emlékeztetünk a szálak nem préselésének hipotézisére).
A fentiekből következik, hogy amikor egy adott ponton a stresszről beszélünk, mindig feltétlenül meg kell jelölni a vágási sík helyzetét, amelyben ez a feszültség merül fel.
Az adott ponton áthaladó végtelen számú, különböző módon orientált helyszínen felmerülő normál és tangenciális feszültségek halmaza jellemzi a stressz állapotot egy adott ponton.
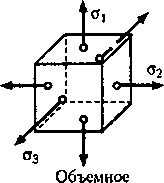
Platform, a kotoryekasatelnye feszültség nulla, on-zyvayutsyaglavnymi párna és feltörekvő normális feszültségek -principal napryazheniyami.Kak bizonyította rugalmasságát, az általános esetben a stressz állapot az övezetben a pont létezhet három egymásra merőleges imno-főtáblán. "
Attól függően, hogy hány ilyen helyek (ahol a * 0), a különbségek a három fő típusa stressz állapot: lineáris (egytengelyű), lapos (biaxiális) iobemnoe (triaxiális) (ábra 20,7.).
A jövőben csak az első két fajta stressz-állapot érdekel.
Nyilvánvaló, hogy a mérlegelt esetben az uniaxialis feszültség, a fő helyek a keresztirányú és a hosszirányú szakaszokban helyezkednek el, azaz egymásra merõlegesek. Figyelünk rá is
hogy a főfeszültségek egy adott ponton maximális és minimális értékkel rendelkeznek ".
A következőkben két egymásra merõleges területre (egy sík gerjesztett állapotra) és a maximális feszültségekre
a tangenciális feszültségek a ferde (a fő) területekhez képest.
Tekintsük a prizma egyensúlyát, amelyre az arcokon fellépő erőket a tengelyeken vizsgáljuk:
Ebből az egyenletből az következik, hogy mikor <р = 45°
Ha abban az esetben sík stressz STI a szomszédságában ezen a ponton lehet kiosztani egy elemi hasáb úgy, hogy annak arca járt csak egyenlő egymással nyíró igénybevételnek (lásd. Ábra. 20,5), akkor ez a fajta stressz állapot további nazyvaetsyachistym sdvigom.V tiszta elmozdulással találkozunk, amikor tanulmányozzuk a körhenger torsolásának elméletét.