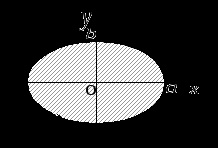
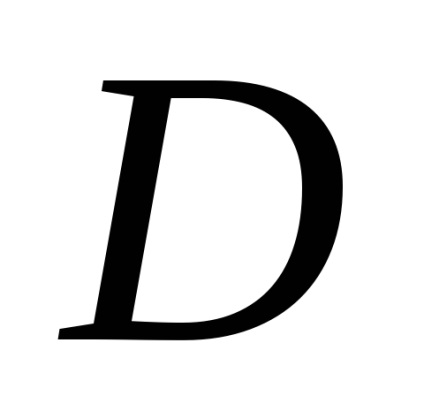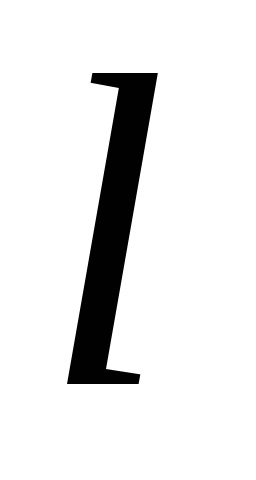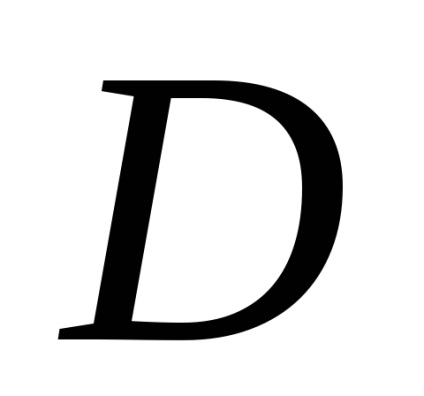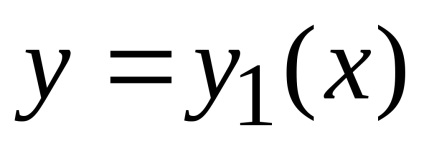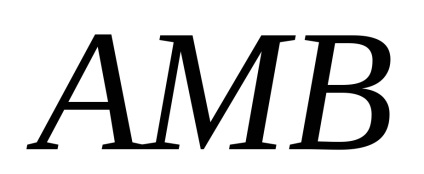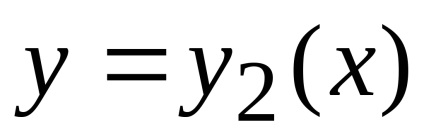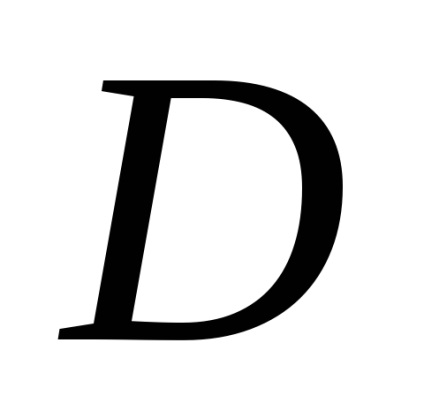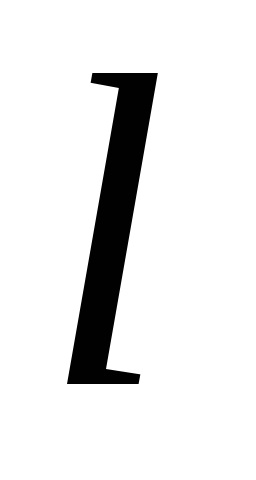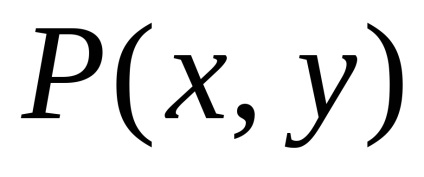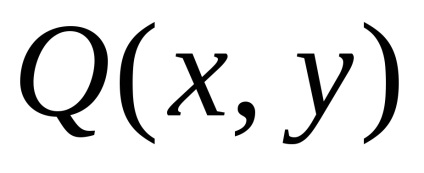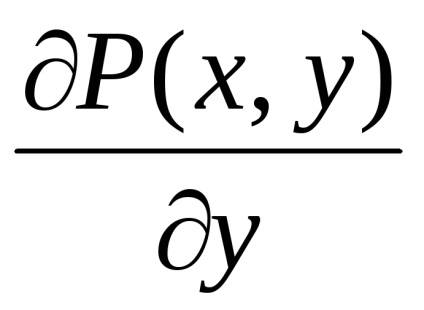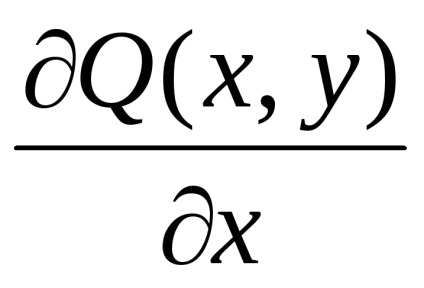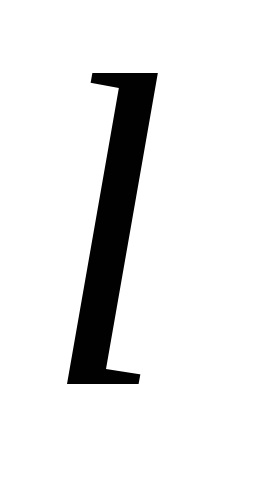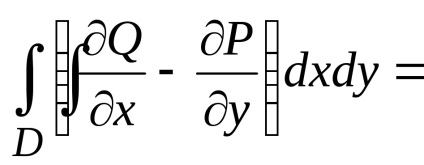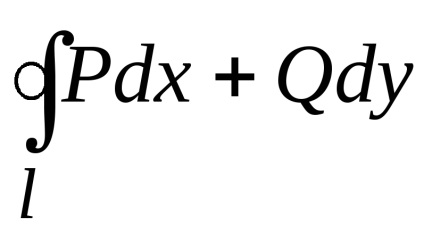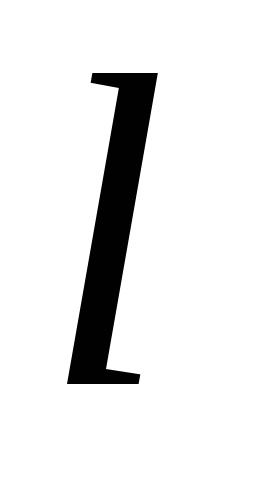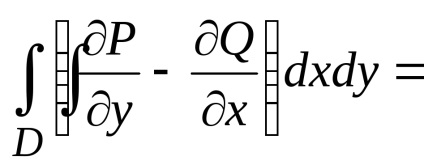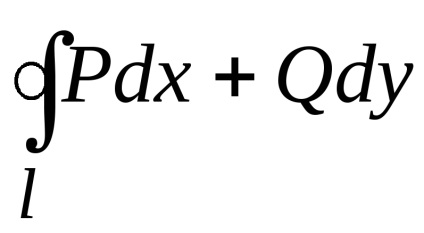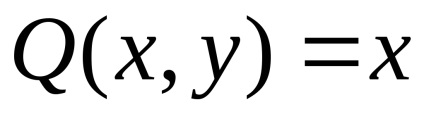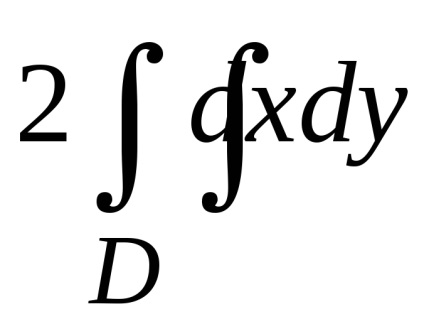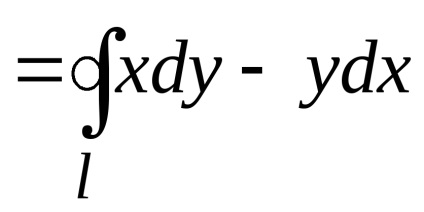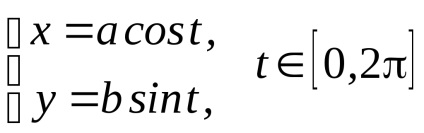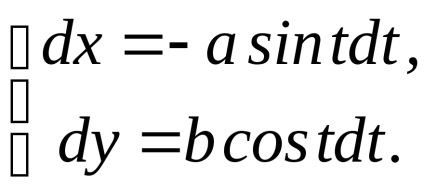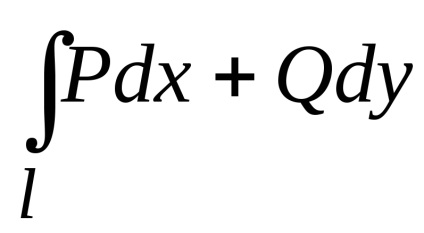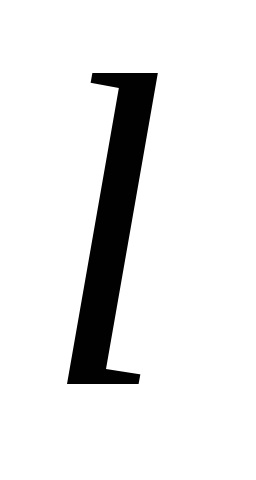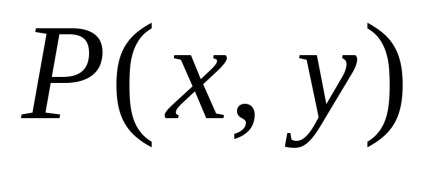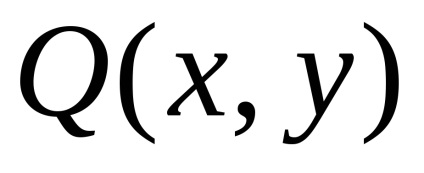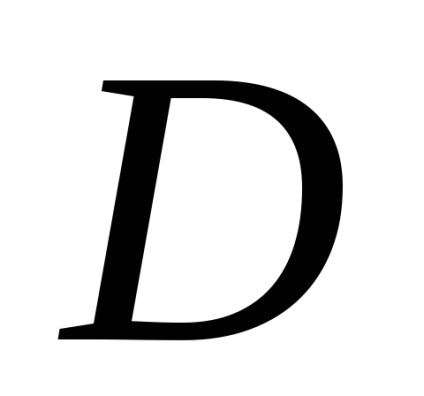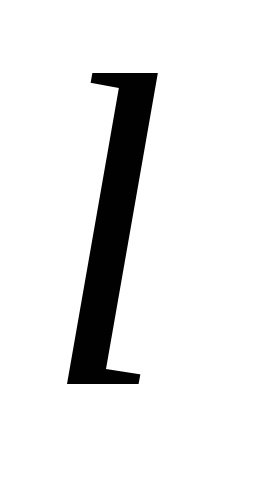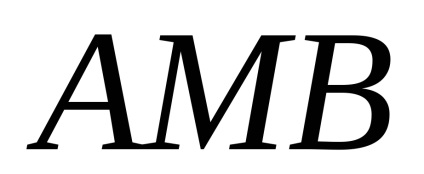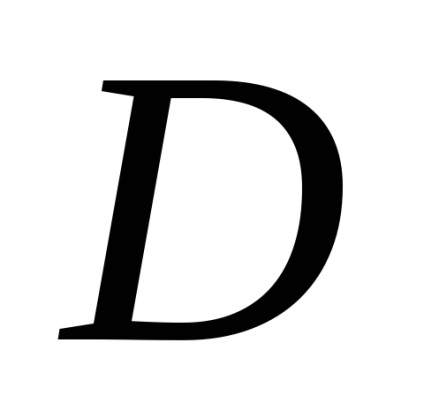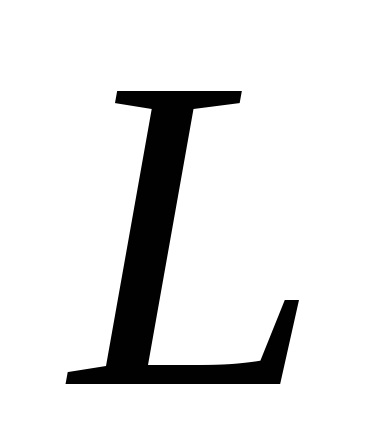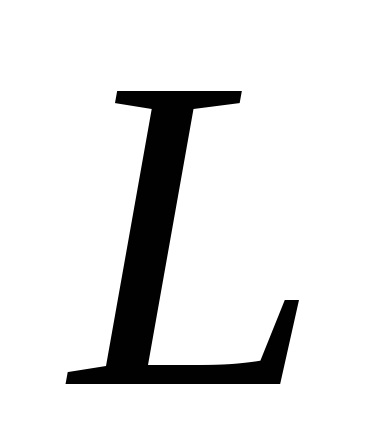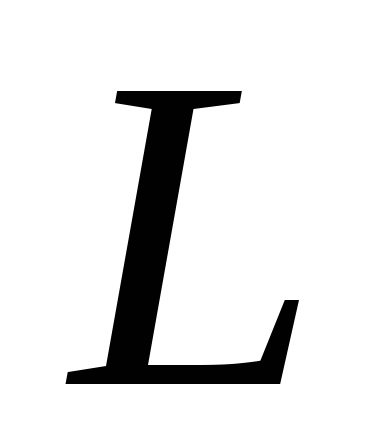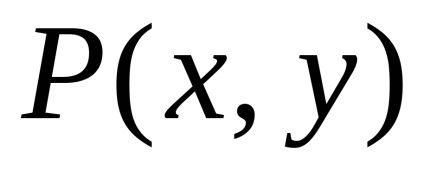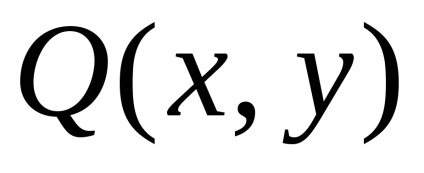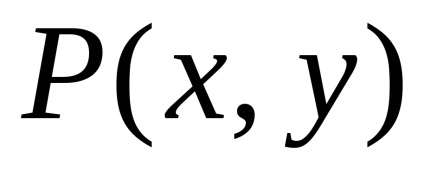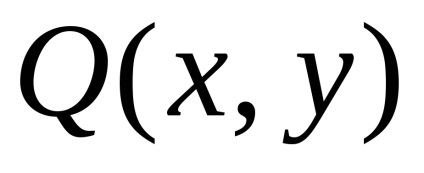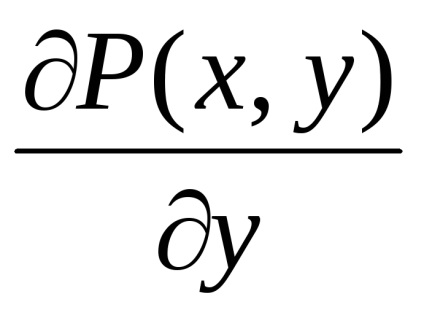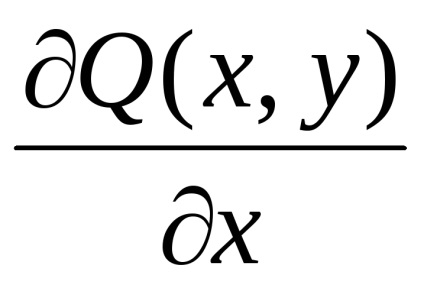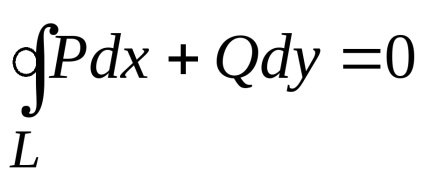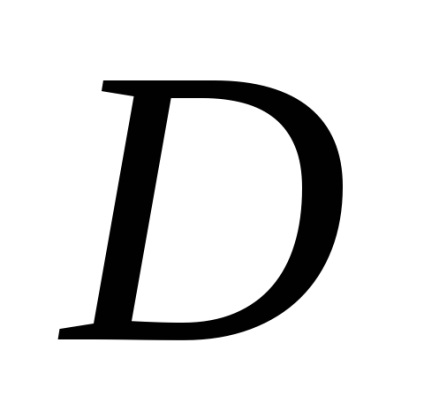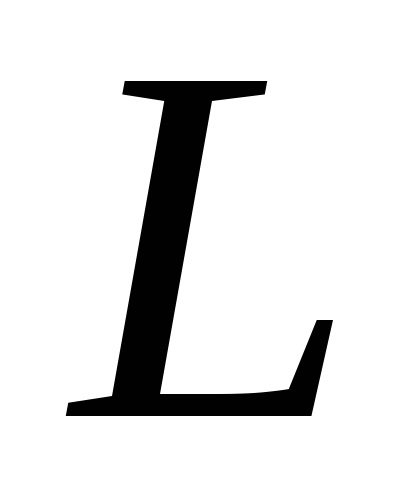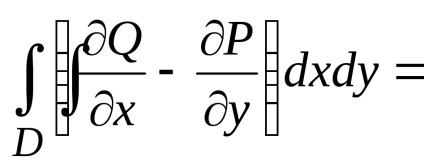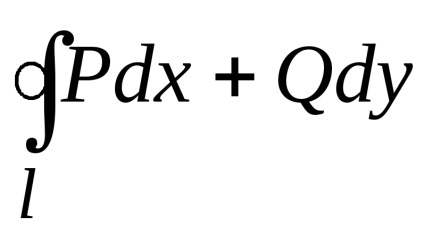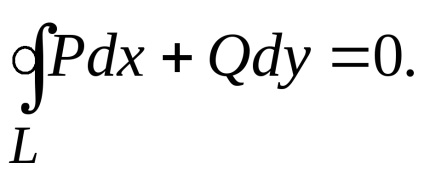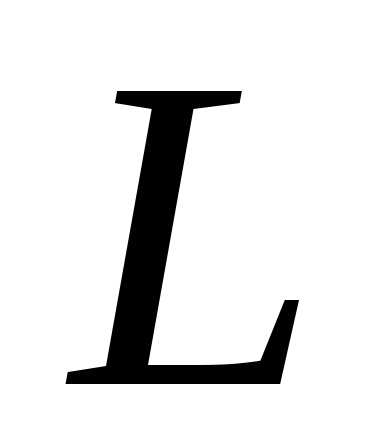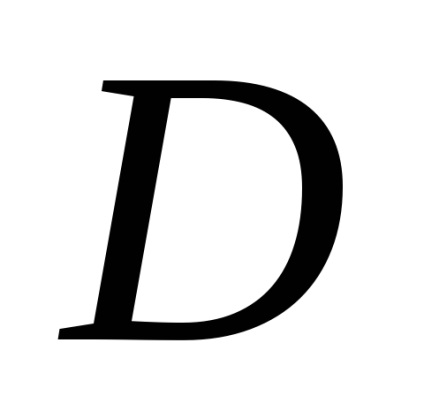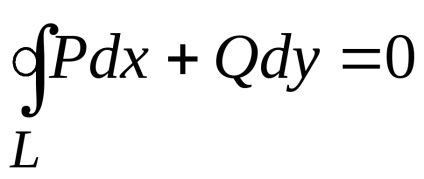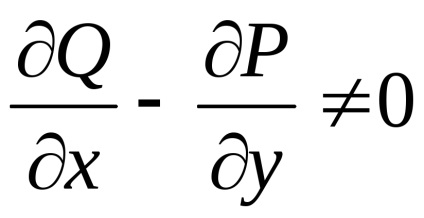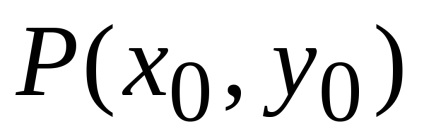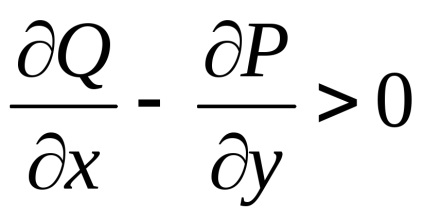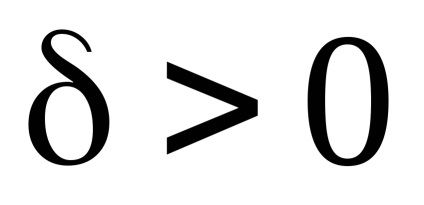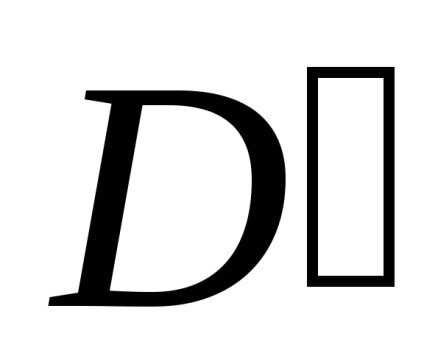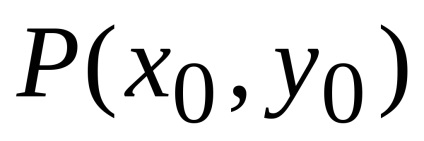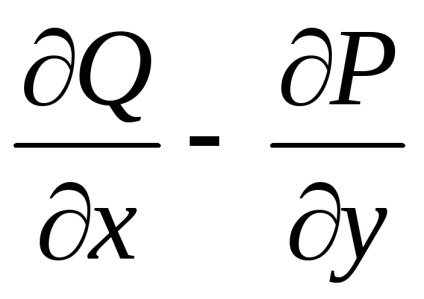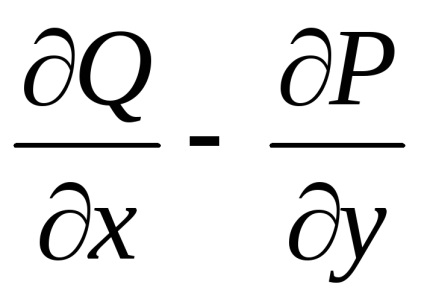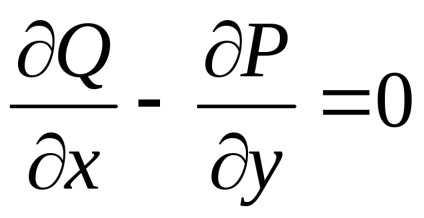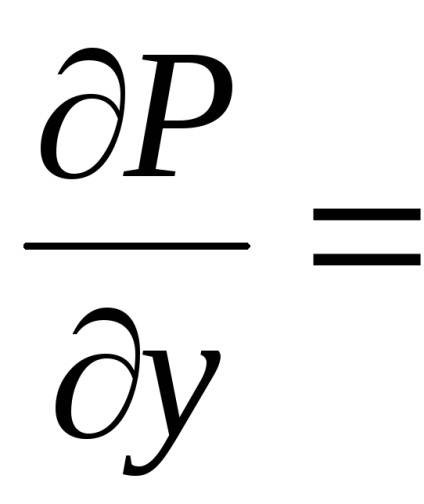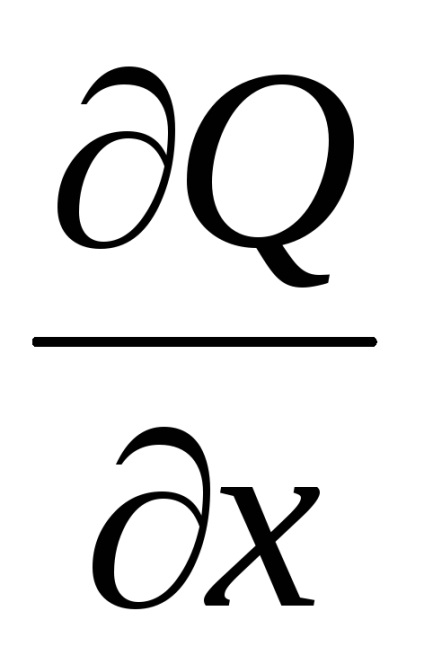A Zöld képlet létrehozza a kapcsolatot a kettős integrációval a domain fölött
és egy görbe vonal mentén a kontúr mentén
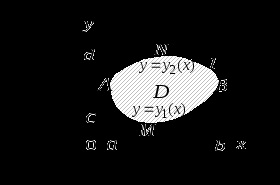
, határolja ezt a régiót. Feltételezzük, hogy a domain
standard az egyes koordináta-tengelyek irányában, és alulról a funkciógrafikon korlátozza
(ív
), fent - a függvény grafikonja
(ív
), amelyek együtt zárt hurkot képeznek
.
Tegyük fel, hogy a domainben
és annak határán
hozzárendelt funkciók
és
a részleges származékaikkal együtt
,
, majd
,
ahol kontúrperiódus
pozitív irányban, azaz az óramutató járásával ellentétes irányba (régió
balra marad). ezért
ahol kontúrperiódus
szintén pozitív irányban zajlik.
Ha a (2) kifejezésből az (1) kifejezéssel elvonjuk a kifejezést, megkapjuk a zöld formulát
.
Megjegyzés 1. Ha egy útvonalat halad át
negatív irányban, azaz az óramutató járásával megegyező irányban (régió
marad a jobb oldalon), akkor a zöld formulája a forma
.
Megjegyzések 2. A Zöld képlet lehetővé teszi egy tartomány területének számítását egy görbe vonalú integrál segítségével. Valójában, ha,
, akkor a zöld képlet átírható az alábbiak szerint:
,
ahol kontúrperiódus
az óramutató járásával ellentétes irányban történik.
Egy példa. Határozzuk meg, egy görbe vonalú integrál segítségével, egy félperselyes ellipszis által körülhatárolt területet
és
.
A megoldás. Az ellipszis paraméteres egyenleteit írjuk le
.
És a (3) képlet segítségével
.
Az integráció útjának görbületi integráljának függetlenségi feltételei
Tekintsük a görbe vonalú integrált elemet
,
átvette a sík görbét
, csatlakozási pontokat
és
.
Feltételezzük, hogy a funkciók
és
folyamatos részleges származékokat tartalmaznak a vizsgált tartományban
. Lássuk, milyen feltételek mellett, a görbületes integrált írás nem függ a görbe alakjától
, de csak az eredeti és a végpontok helyzetétől függ
és
.
Vegyünk két önkényes görbét
és
, a vizsgált régióban fekszik
és csatlakozási pontokat
és
. enged
.
Ezután a görbületi integrálok 1. és 2. tulajdonságai alapján:
,
azaz egy kanyargós, egy zárt kontúr felett
Az utolsó képletben a görbe vonalú integrál egy zárt kontúr mentén történik
, görbékből áll
és
. Ez az áramkör
nyilvánvalóan önkényesnek tekinthető.
Így abból a feltételből, hogy bármely két pontot
és
a görbe vonalú integrál nem függ az összekötő görbék alakjától, hanem csak ezeknek a pontoknak a pozíciójától függ, ebből következik, hogy a kanyargós illesztés bármely zárt kontúrra nulla.
Az ellentétes is igaz: ha a kanyargós illesztés bármely zárt kontúr fölött nullával egyenlő, akkor ez a görbe vonalú integrál nem függ a két tetszőleges pontot összekötő görbe alakjától, de ezektől a pontoktól függ. Valójában az egyenlőség (2) egyenlőséget jelent (1).
Természetesen felmerül a kérdés: milyen feltételeknek kell a funkciók
és
úgyhogy a görbületi integrál minden zárt kontúr fölött nullával egyenlő. A kérdésre adott válasz a következő tételből áll:
Tétel. Tegyük fel, hogy valamilyen tartomány minden pontján
funkciók
és
a részleges származékaikkal együtt
,
folyamatosak. Ezután annak érdekében, hogy a görbületes integrál minden zárt kontúr fölött
, ebben a térségben fekvő, nulla volt,
,Szükséges és elegendő az egyenlőség
a régió minden pontján
.
Bizonyítás. Vegyünk egy tetszőleges zárt hurkot
a D tartományban, és jegyezze fel a zöld formulát:
.
Ha a feltétel (3) teljesül, akkor a kettős integrál a bal oldalon azonos, nulla,
Tehát a (3) feltétel elegendő.
Most igazoljuk ennek a feltételnek a szükségességét; azt bizonyítjuk, hogy ha (2) bármelyik zárt görbéhez tart
területén
, akkor a (3) feltétel teljesül ezen a ponton.
Tegyük fel, hogy éppen ellenkezőleg, (2) elégedett,
,
és a feltétel (3) nem rendelkezik,
legalább egy ponton. Legyen például egy bizonyos ponton
.
Mivel az egyenlőtlenség bal oldala folyamatos funkciót tartalmaz, pozitív lesz és nagyobb, mint egy bizonyos szám
minden eléggé kis tartomány minden pontján
, egy pontot tartalmaz
. Ezt a kettõs integrált szerepet választjuk a különbségnek ebben a régiójában
. Értékes lesz. Tény, hogy
.
De a zöld képlet alapján az utolsó egyenlőtlenség bal oldala egyenlő a határvonal mentén a görbe vonalú
mezője
, amely feltételezés szerint nulla. Következésképpen az utolsó egyenlőtlenség ellentmond a (2) feltételnek, és így a feltételezés, hogy
legalább egy ponton nem nulla, hamis. Ebből következik
a régió minden pontján
, és ezért
.
Kapcsolódó cikkek