Mikroszkóp nagyításának meghatározása és a kis tárgyak lineáris méreteinek mérése
Eszközök és tartozékok:
egy biometrikus mikroszkóp, egy megvilágító, egy mikrométer, egy milliméteres vonalzó, egy vékony vezetékkel ellátott csúszda, egy hajszálas csúszda, egy csíkos izom szövettani előkészítése és egy kép vázlatának támogatása.
mikroszkóp tanulmányozására, egy mikroszkóp nagyításának és egy kis objektum lineáris méretének meghatározására.
A kézikönyvben használt optika fogalmai:
1. A lencse átlátszó, két gömbös felület által határolt test, az egyik felület sík lehet.
Vékony lencsék - olyan lencse, amelynek vastagsága kicsi a görbület sugaraival összehasonlítva.
Optikai rendszer - több lencse rendszere.
A lencse fő optikai tengelye egyenes vonal, amely áthalad minden gömbfelületének központján.
A rendszer fő optikai tengelye egy egyenes, amelyen minden gömbfelületének központjai fekszenek.
A gyűjtőlencse egy olyan lencse, amely egy párhuzamos sugár sugarát átalakítja rá egy közelítő sugárra.
A vékony lencsék optikai középpontja a fő optikai tengelyen található pont, amelyen keresztül a fénysugár az irányváltoztatás nélkül áthalad. Általában egybeesik a lencsék geometriai középpontjával.
A szem optikai középpontja a modell szemének hagyományos pontja, amikor a sugáron áthaladva nem változik az iránya.
A lencse fókuszpontja az a pont, amelyen a sugarak a reflexió után keresztezik egymást, a fő optikai tengelyével párhuzamosan. A gerenda terjedésének irányával összhangban az első és a hátsó fókuszpontok megkülönböztethetők
A fókuszsíkok olyan síkok, amelyek a lencsének a fő optikai tengelyére merőleges főmeccsén haladnak keresztül. A fókuszsíkban a fő optikai tengely bármely szöget bezáró párhuzamos sugarai metszenek.
A fókusztávolság a vékony lencsének optikai középpontjától a fókuszpontig terjed.
A legjobb nézet távolsága a szemtől szemben a legrövidebb távolság, amelynél a szem éles képet ad a minimális szállásfeszültségről. Normál szemmel 25 cm.
A látószög az objektum legkülső pontjaiból érkező sugarak által alkotott szög, amely a szem optikai középpontján keresztül történik.
Az immersziós rendszer egy mikroszkóp célja, amelyben az első lencse és a vizsgált tárgy közötti tér egy nagy törésmutatójú folyadékkal tölthető be, amelyet merítésnek neveznek.
Optikai rendszer és a mikroszkóp működésének elve
A mikroszkóp két rövidlátófókuszú optikai rendszer - objektív és okulár kombinációja.
lencse - néhány milliméter,
okulár - néhány centiméter.
A mikroszkóp optikai rendszere és a benne lévő sugarak útvonala a 3. ábrán látható. A fókusztávolság és a cső optikai hosszának aránya feltételesen van kiválasztva.
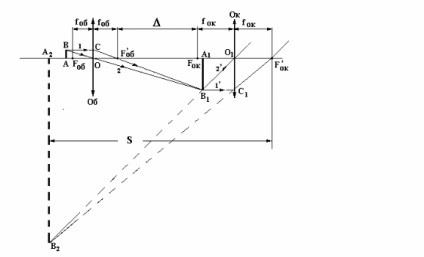
A lencsét és a szemlencsét két gyűjtőlencse Oh és Ok formájában ábrázolja. Egy kis AB objektumot helyezünk az objektum színpadára a lencse előtt, kissé nagyobb távolságra, mint a gyújtótávolság.
Az 1. ábrán látható kép a vékony lencsék képének szerkesztésére vonatkozó szabályoknak megfelelően készült, a legegyszerűbb esetben. Ha az objektum a fő optikai tengelyen van. Beam 1 megy a B pontból párhuzamosak a fő optikai tengely és OO1 után fénytörés lencse áthalad a hátsó fő hangsúly FOB. Beam 2 megy a B pontból, anélkül fénytörést keresztül optikai középpontja a lencse A. A metszéspontja a sugárzás rejlik B1 pont - a kép a B pont Mi csepp merőleges, hogy pont a fő optikai tengelyre, és kap pontot A1 A1 B1 közbenső kép.
Így egy objektív objektív segítségével egy valós, nagyított, inverz közbenső képet kapunk a síkban, amely feltétlenül a Fock szemlencse előrehaladó főfókusza mögött fekszik.
Hasonlóképpen, az 1 'és a 2' sugár használatával a szemlencse által létrehozott végleges képet készítjük. A szemlencse fénytörése után ezek a sugarak divergens sugarat alkotnak, ezért nem metszenek egymással. Folytassuk őket az ellenkező irányba, a B2 kereszteződési pont a B1 pont képzeletbeli képe. és a szegmens A2 B2 - a végleges képet az objektum AB, megnagyobbodott, képzeletbeli és inverz az objektumhoz képest, fekvő tartományában a legjobb S. Ez a kép, és megvizsgálja a szem: egy széttartó köteg sugarak 1 „és 2” a szemlencse belép a szembe, akkor megtörik az optikai rendszer által, és valódi képet képez a retinán. Amikor dolgozik mikroszkóp szem van elhelyezve, hogy az optikai középpontja egybeesik a hátsó fókusz elsősorban szemészeti Fok. Ezért a legjobb látás távolságát feltételesen mérik ebből a pontból.
A mikroszkóp által adott nagyítás azt mutatja, hogy hányszor az objektum képének értéke nagyobb, mint az objektum értéke (1. ábra)
Az OCF'ob és az A1 B1 F'ob háromszögek és az AB = OS, F'ob A1 egyenlők hasonlóságából
ahol - a cső optikai hosszúsága - a lencse hátsó fókusza és a szemlencse első fókusza közötti távolság; S a legjobb nézet távolsága; FOB. a lencse és a szemlencse fókusztávolsága. Miután a (3) és (4) képletet a (2) kifejezéssel helyettesítjük, a kapott vegyületet kapjuk
A lencse és a szemlencsék nagyítása a peremén látható, például a lencsén: 8,20,40,60; a szemlencsén: 7x, 10x, 15x.
A MIKROSCOPE FELHÍVÁSA
A mikroszkóp felbontási ereje mikroszkóp tulajdonsága, hogy külön képet adjon a vizsgált tárgy apró részleteiről.
A felbontási határ a legkisebb távolság két pont között, amely külön-külön látható mikroszkópban.
Minél kisebb a felbontási határ, annál nagyobb a mikroszkóp felbontási ereje. A felbontási határ meghatározza az alkatrészek legkisebb méretét, amely mikroszkóp segítségével különböző lehet a készítményben.
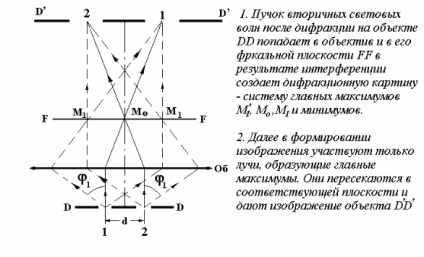
A mikroszkóp felbontásának elméletét a Jena-i K. Tseis-i üzem igazgatója dolgozott ki, az E. Abbe professzor-optikus (1840-1905). Egyszerű mikropreparációként diffrakciós rácsot vett, mikroszkópban tanulmányozta a képalkotás mechanizmusát, és a következőket mutatta.
Bemutatjuk a nyílásszög fogalmát - ez a szög a kúpos fénysugár extrém sugarai között, amely az objektum közepétől a célig halad (3a. Ábra).
Egy kép létrehozásához, vagyis egy objektum feloldásához elegendő, ha a sugarak az objektívlencsét érintik, és legalább az egyik oldali nullát és elsőrendű maximumot alkotnak (2. és 3. ábra). Részvétel a magasabb magasságú sugarak képződésében növeli a kép minőségét és kontrasztját. Ezért a maximálisan képződő sugaraknak a tárgy rekesznyílásán belül kell lenniük.
Így, ha az objektum egy diffrakciós rács egy időszak d, és a beeső fény ez normális (2. ábra és a 3b), a kép kialakulása kell részt sugarai képező maximumai nulla, és elsőrendű mindkét oldalról, és az a szög 1 - szög az első sorrendet alkotó sugarak eltérései szélsőséges esetben egyenlőnek kell lenniük az U / 2 szöggel. Ha veszünk egy kisebb rács időszak d”, akkor '1 szög nagyobb, mint a szög U / 2, és a kép nem fordul elő. Ezért osztásperiódus d lehet venni, mint a felbontás határa a mikroszkóp Z. Ezután a rács képlet, írunk k = 1 :. A d helyett Z, és 1 U / 2, akkor megkapjuk (6)
Mikroszkópos eljárás során a fénysugarak különböző szögben esnek az objektumra. A Ferde beesés sugarak (Ris.3g) felbontású határérték csökken, mint a kép kialakulása magában csak a sugarak, hogy létrehozzák a maximumai nulladrendű és elsőrendű egyfelől, és az a szög 1 egyenlő lesz a nyitási szög U. A számítások azt mutatják, hogy a képlet a A felbontási határ ebben az esetben a következő formában van
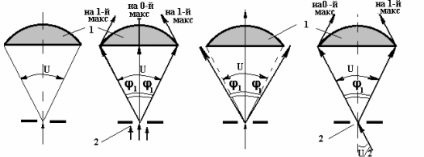
1 - az objektív első lencséje, 2 - az objektív.
Ha az objektum és a tárgy közötti tér egy n törésmutatóval rendelkező merülő közeggel van töltve, amely nagyobb, mint a levegő törésmutatója, akkor a fény hullámhossza n = n. Ha ezt a kifejezést a felbontási határérték (7) képletébe helyezzük, akkor megkapjuk
Így a (7) képlet meghatározza a száraz célra szolgáló mikroszkóp felbontási határát és a (8) képletet egy merülési célú mikroszkóp számára. A fenti képletekben a sin0.5U és nsin0.5U értékeket az objektívlencse numerikus nyílásának nevezik és az A. betűvel jelöljük. Figyelembe véve ezt, a mikroszkóp felbontási határértéke általában az alábbiak szerint van leírva. (9).
Amint látható képletekkel (8) és (9), a felbontás mikroszkóp függ a fény hullámhossza, a nagysága egy nyitási szög, a törésmutatója a közeg között a lencse és a tárgy, a beesési szög a fénysugarak a tárgyat, de független a szemmel kapcsolatos paraméter. A szemlencse nincs további információt a szerkezet a tárgy nem a kép minősége nem javul, akkor csak növeli a közbenső kép.
A mikroszkóp felbontása javítható egy merítéssel és a fény hullámhosszának csökkentésével.
A merülés használatakor a felbontás növelése az alábbiak szerint magyarázható. Ha a lencse és a tárgy levegő (száraz lencse), a fénysugár az átmenet során a fedőlemez a levegőbe közeget egy kisebb törésmutatójú, jelentősen megváltoztatja az irányát eredményeként a fénytörés, ezért kevésbé gerenda belép a lencse. Amikor a merítés közeget, amelynek törésmutatója körülbelül megegyezik a törésmutatója az üveg, a változó az utat a sugarak a környezetben nem megfigyelt és a nagyszámú sugarak belép a lencse.
Mivel a bemerítés folyékony take víz (n = 1,33), cédrus olajat (n = 1,515) és mások. Ha a maximális nyitási szög a modern lencsék 140 eléri a 0, a száraz lencse A = 0,94, és a lencse olajjal merítés A = 1,43. Ha a számítás a fény hullámhossza használt = 555 nm, amelyre a szem a legérzékenyebb, majd a felbontás határa a lencse száraz 0,30 mikron, és olaj immerziós - 0,19 mikron. A numerikus rekeszérték értéke a lencsetartón: 0,20; 0,40; 0,65 és mások.
Az optikai mikroszkóp felbontásának növelésével a fény hullámhosszának csökkentésével ultraibolya sugárzás alkalmazásával érhető el. Ehhez vannak speciális ultraibolya mikroszkópok kvarcoptikával és eszközök megfigyelésére és fényképezésére. Mivel a szóban forgó mikroszkópokban a fényt körülbelül kétszer kisebb, mint a látható fény hullámhosszán használják, képesek körülbelül 0,1 μm méretű gyógyszerszerkezetek feloldására. Az ultraibolya mikroszkóp további előnye - a festetlen készítmények vizsgálata. A legtöbb biológiai tárgy látható fényben átlátszó, mivel nem veszi fel. Azonban szelektív abszorpcióval rendelkeznek az ultraibolya-tartományban, és ezért könnyen megkülönböztethetők az ultraibolya sugárzástól.
A legnagyobb felbontás egy elektronmikroszkópban. Mivel az elektron mozgása során az hullámhossz 1000-szer kisebb, mint egy fényhullám hossza.