Interpolációs kvadratúra formulák
Interpolációs kvadratúra formulák
3. fejezet. Numerikus integráció
A numerikus differenciálásban a függvény szoros értékeit kell elvonni egymástól. Ez az első jelentős számok megsemmisüléséhez vezet, azaz a szám hiteles jeleinek egy részének elvesztéséhez.
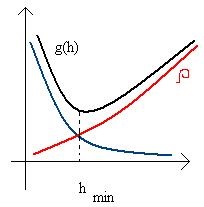
# 961; meghatározza a módszer hibáját, és határozatlan ideig csökken h → 0 -ként. Ugyanakkor a f (x) függvény kiszámításakor a hibával kapcsolatos visszaélhetõ hiba is létezik :. Kötés nélkül növeli h → 0 értéket.
Így a teljes hiba nem haladja meg. Ezért az optimális lépés a legkisebb g (h) -nek megfelelő módszer.
Egy kisebb lépés nem nyereséges, és kisebb hiba nem érhető el. Ez a minimális hiba kisebb, annál kisebb a bemeneti adatok hibája.
A probléma az integrál hozzávetőleges számításából áll. például az x1 csomópontok f (x) függvényének diszkrét értékeiből. xn. egy függvénynek a hozzá közelítéssel való helyettesítésére stb.
Tehát az integrált összeg. A közelítő összegek általános nézete. ahol Ak egy bizonyos együtthatók.
Legyen feltétlenül egy meghatározott integrált,
ahol f (x) az x1 ... xn csomópontokban meghatározott diszkrét függvény;
q (x)> 0 egy súlyfüggvény.
Ezután a hozzávetőleges számítási képletnek az a formája:
Az (1) jobb oldala kvadratúra.
Az alábbi megközelítés alkalmazható: az f (x) függvényt az x1 ... xn csomópontok Pn-1 (x) interpolációs polinomával közelítjük.
Ebben az esetben megkapjuk az (1) képletet és a szükséges integrál kvadratúráját.
Feltételezzük, hogy. Kapunk :.
- interpolációs polinom Lagrange-ben,
A f (x) függvény helyett az (1) polinomiális Pn-1 (x) helyettesítését kapjuk:
A hiba ebben az esetben az alábbi formában reprezentálható:.
Az építés során az interpolációs kvadratúra formula pontos,
1. tétel A kvadratúra-formula (1) pontos bármely Pk (x) polinom esetében,
k ≤ n-1 ha és csak akkor, ha interpoláció van.
Legyen az (1) képlet pontos legyen minden Pk (x), k ≤ n-1 polinom esetében, azaz.
Bizonyítsuk be, hogy az Ak ezt a (2) képletben találjuk meg.
Fontolja meg a függvényeket - fokú polinomok (n-1):
Ezután az egyenlőség: i. Az Ai-t a (2) képlettel számoljuk.
Az (1) képletnek interpolációs képletnek kell lennie, azaz. Az Ak értékeket (2) számítják ki. Bizonyítsuk be, hogy az (1) pont minden Pk (x), k ≤ n-1 polinom esetében pontos.
Vegyünk egy tetszőleges Pk (x), k = n-1 polinomot.
A Lagrange formájában való képviselete a következőképpen alakul:
Másrészt a kvadratúra
, ahol az Ak-ot a (2) képlet alapján számítjuk ki, i = J.
Amint bizonyítani kell.
Értékeljük az interpolációs típus kvadratúra-képletének hibáját: