Módszerek egy anyagpont, sebesség, gyorsulás - stadopedia mozgásának meghatározására
Egy pont mozgásának meghatározása annak érdekében, hogy beállíthassa pozícióját az egyes időpontokban. Ezt a pozíciót meg kell határozni, ahogy azt korábban már említettük, bármely koordinátarendszerben. Azonban nem kell mindig megadnia a koordinátákat; olyan értékeket használhat, amelyek valamilyen módon kapcsolódnak hozzájuk. A pont mozgásának meghatározására három fő mód van az alábbiakban.
1. A természetes út. Ezt a módszert akkor használjuk, ha a pont mozgásának pályája ismert. A pálya olyan térbeli pontok gyűjteménye, amelyen keresztül egy mozgó anyag részecske halad. Ez az a vonal, amelyet az űrben húz. A természetes módszerrel meg kell adnia (1. ábra):
a) a mozgás pályája (bármely koordinátarendszerhez viszonyítva);
b) tetszőleges pont van nullára, amiből az S távolságot a mozgó részecske méri a pályán;
c) az S minta pozitív iránya (ha az M pont az ellenkező irányba mozdul el, S negatív);
d) a t időpont eredete;
e) az S (t) függvényt, amelyet a pont mozgásának jogának ** nevezünk.
2. Koordináta módszer. Ez a leginkább egyetemes és kimerítő módja a mozgalom leírásának. Ő javasolja a feladatot:
a) koordinátarendszer (nem szükségszerűen Descartes) q1, q2, q3;
b) a t idő eredete;
c) a pont mozgásának jogát; függvények q1 (t), q2 (t), q3 (t).
Egy pont koordinátáiról beszélünk, akkor mindig szem előtt tartjuk (hacsak másként nem jelezzük) a Descartes-koordinátákat.
3. Vektoros út. Egy térbeli pont helyzetét meghatározhatjuk egy adott eredetből egy adott pontra húzódó sugárvektorral (2. ábra). Ebben az esetben a mozgás leírásához meg kell adnia:
a) az r sugárvektor eredete;
b) a t idő eredete;
c) az r (t) pont mozgásának jogát.
Gyorsuláspont. [m / sec2]. Ss.-I előrejelzések stb. Modul usk.-y. célja. koszinuszok. és így tovább.
Amikor megadja a mozgást a polárkoordinátákban: a gyorsítás sugárirányú vetülete. keresztirányú. gyorsító modul. A természetes sp. A mozgási feladatok teljes gyorsulása a normál és a tangenciális (tangenciális) gyorsulásra bomlik. Normál gyorsítási modul. r a pályának a görbületi sugara, a normál gyorsulás a normális irányba halad a pályához (^ az érintőhöz) mindig a görbület középpontjáig; a konkáv irányába. A normál gyorsulás jellemzi a sebesség változását az irányba. A tangenciális gyorsító modul. A pályát érintő tangens irányában, akár fordulatszámon, akár fordított irányban. A tangenciális gyorsulás jellemzi a sebesség változását nagyságrendben. Gyorsított mozgással az érintő iránya. USK. és a sebesség ugyanaz, míg a lassú fordulatszám az ellenkezője. ^. Þ. A gyorsító vektor a folytonos síkban van Þ a binormálra vetített vetület 0 (a fő normális a folytonos síkban van, vagyis a síkgörbe síkjában, a binormális a fő normalhoz és a tangenshez). A pont mozgásának egyes esetei:
1) Egyenes vonal: görbületi sugár r = ¥ (végtelenül nagy) Þ a = 0, a = az.
2) Egyenletes görbületi mozgás: v = const Þ = 0, a = an. Usk. csak a sebesség irányának megváltozása miatt jelenik meg. A mozgás törvénye: s = s0 + v × t, az s0 = 0 v = s / t esetében.
3) egyenletes egyenes vonalú mozgás: a = at = an = 0. Az egyetlen mozgás, ahol a = 0.
4) egyenlő görbületi mozgás: at = const, v = v0 + at × t. Ha egyenlő. az és a v jelzései azonosak, és másképpen lelassulva a jelek eltérnek.
Tétel. Egy merev test transzlációs mozgása során minden pontja ugyanolyan és párhuzamos pályák mentén mozog, és minden egyes pillanatban azonos nagyságú és irányú sebességgel és gyorsulással rendelkezik.
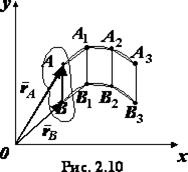
Bizonyítás. A tétel bizonyításához egy vonalszakasz mozgását vesszük figyelembe. amelyet a transzlációs mozgást végző testben végzünk (2.10 ábra). A transzlációs mozgás meghatározásából következik, hogy minden adott pillanatban a szegmens. egymás után elfoglalt pozíciókat. . és így tovább. párhuzamos marad az eredeti helyzetével. Tekintettel erre és az a tényre, hogy. arra a következtetésre jutunk, hogy a törött vonalak párhuzamosak, és ha alkalmazzák őket, egybeesnek minden pontjukkal. A szegmens megfontolt pozíciói közötti időintervallumok végtelen csökkenésével látjuk, hogy a pont és a pont ugyanazokat a görbéket írja le, vagyis az átfedésnek egybeeső görbéket.
A tétel második részének bizonyításához megjegyezzük
Az időt a jobb és bal oldali származékokat vesszük
A fenti tétel lehetővé teszi számunkra azt a következtetést, hogy a merev test transzlációs mozgását teljesen meghatározza bármely pontjának mozgása