Mérési módszerek
A mérési módszer olyan technikák halmaza, amelyek biztosítják a mért fizikai mennyiségnek a mértékegységgel való összehasonlítását.
A mérési módszerek a mérési objektum és a mérőeszköz közötti kölcsönhatás fizikai elvein alapulnak a mérési adatok megszerzéséhez megengedett hibával.
Megkülönböztetik a mérési módszereket:
1) a mérés fizikai elvén (mechanikus, pneumatikus, akusztikus, optikai, elektromos stb.);
2) a mérőeszközök típusának mérőszáma (analóg (a megfelelő függvény folyamatos) és digitális (a függvény kvantált);
3) a mért fizikai mennyiség és mérték összehasonlításának módszerével megkülönböztetik a közvetlen értékelési és összehasonlítási módszerek módját.
A közvetlen értékelés legelterjedtebb módja, amelyben fizikai értéket a mért érték egységeiben előretöltött eszközök (közvetlen mérések) vagy több (közvetett mérés) bizonysága alapján ítélnek meg.
Az összehasonlítási módszereknél a mért értéket összehasonlítjuk egy olyan mérőeszközzel, amely kívül esik a mérési eszközön.
Tüntesse fel a differenciálódási módszert, ahol a mért értéket az egyes standardokkal való különbség alapján ítélik meg.
Vegyünk egy U-alakú folyadékmérőt, amelynek mért értéke Px nyomás (88. ábra).
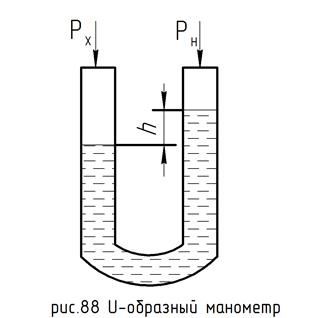
A Px nyomást az alábbi képlet adja meg:
Ha Px> PH. akkor a megfelelő folyadékot az intézkedéshez csatlakoztatott csőbe (standard) kinyomjuk.
A különbözeti módszereknél azt feltételezzük, hogy a mért mennyiség összehasonlításának pontosabb értéke, mint maga az érték - Px. így a hiba beágyazódik a mérésbe .. # 961; gh, vagy inkább, hogy az, hogy meglehetősen pontosan ismert sűrűsége és gravitációs gyorsulás, a teljes hiba a magasságának mérésére - h, és a több, ez a magasság, annál kisebb a hiba.
A Px és a PH közötti különbségnek a lehető legkisebbnek kell lennie, ezért növelni kell a h magasságot, például amikor egy rakétamotor égéskamrájában a nyomást mérjük, ezt a sűrűség csökkentésével érjük el - # 961; - a víz helyett olaj használatos, vagy a kar lejtése piezométer, ha a magasságmérés hibája 1,5 m magas cső jelenlétében kb. 1 mm, akkor a hiba 1 mm / 1500 lesz. Jelenleg a PH nyomását nagy pontossággal mérik, így a differenciálmű módszer lehetővé teszi a Px nyomás pontosabb mérését. azaz manométerrel.
A differenciális forma egy változata a nulla módszer. amikor a mérőeszköz mért értékkel töltött állapotban visszatér eredeti helyzetébe.
A vizsgált példában a mennyiség # 961; gh → 0, mivel h = 0. Hiszterézis nincs jelen, a bal váll a jobb utáni ki - a felületi feszültség a folyadék marad a falon, és, természetesen, hogy a mért értékek torz, ha a nyomás egyensúlyt Px. t. e. a nyomás PH cserélje változó nyomást, amely képes pontosan mérni, az oszlopok visszatér az eredeti helyzetébe, és a paraméterek az energia disszipációs lesz jelen.
A nulla módszer pontosabb, mivel a hiba elsősorban a szabványban koncentrálódik, vagyis a szabvány hibája, így a hiba ennek a módszernek.
A helyettesítési módszerben a mért értéket a mérési jel változása alapján ítélik meg, amikor a mérési objektumot egy szabvány helyettesítik.
Tekintsünk egy betöltött fékpadot, amely tömegegységekben végzett (89.
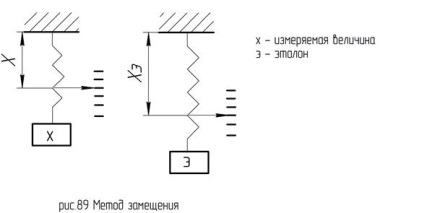
A mért érték helyett a mérőeszközt egy standarddal töltjük be.
A mért mennyiséget a kapcsolat alapján ítéljük meg:
Minél pontosabb a mért értékre való hivatkozás, annál pontosabb a mérés.
A véletlen módszerben a mért mennyiség és a reprodukált mérés közötti különbséget bármely periodikus jel, például a skálaértékek (féknyergek) egybeesése határozza meg.
§ 27.7. A mérések pontossága és pontossága. Alapfogalmak. A mérési hibák típusai.
A mérési hiba a mért () és az ideal () értékek közötti különbség.
Nem ismerjük az ideális mennyiség jelentését, akkor a tényleges hiba fogalmát használjuk:
- egy adott mérés során a lehető legnagyobb pontossággal meghatározott mennyiség.
Pontos eszköz nem használható a közvetlen gyakorlati mérések, különösen nyomás méréséhez a az égéstérben használhatja a dugattyú manométer, amely lehetővé teszi a magas fokú pontosság határozza meg a nyomást, de magában hordozza a hosszú fagyasztva statikus feltételek, így használata piezometrikus érzékelőt, amely rákerül a készülék karja, és az értéket egy dugattyús mérővel végzik el, így a tényleges nyomásérték található, ezért lehetséges a tényleges hiba meghatározása és a mért érték értékét egy másik nyomásmérő vagy -érzékelő értékének megfelelően olvassuk le.
Megkülönböztetni a származási helyen a mérési láncban, objektív és szubjektív hibákat.
A cél:
1) hangszeres (a skálaeszköz nyíljának elmozdítása stb.);
2) telepítés (nem horizontális, nem párhuzamos, stb.);
3) a mérési módszer hibája (a mozgó közeg hõmérsékletének mérése nyílt csomóponttal ellátott termoelem segítségével) a legnehezebb, a mechanikai folyamatok alapos ismerete szükséges az elimináláshoz;
4) elméleti -. Mérésekor a valós mért tárgy helyébe egy bizonyos modell e modell helyesen kialakított, akkor tenni módszeres elméleti hibákat. Például, meg kell találni a terület a kritikus szakasz a rakéta, azt feltételezzük, hogy van egy egyszerű forma, de a méretei után a motor indításakor, a fúvóka melegítjük, mert - köszönhetően a hőmérséklet és a képlékeny válik különböző alakú, és a kritikus keresztmetszeti területe nehezen mérhető.
A szubjektív hibák a megfigyelő tulajdonságaihoz kapcsolódnak (dinamikus jellemzők).
Az interferencia (változhatatlan értékek) hatása különbözteti meg az alap és a további hibát.
Ezen értékek tartománya (nyomás, környezeti hőmérséklet, stb.) A műszer útlevelében található, amelyen belül a mérési hiba nem haladja meg a megadott értéket. Számos esetben rendelkezésre áll egy ilyen tartomány bővítési területe, ami egy további hibát okoz (például hőmérsékleti hibát).
Ha az útlevél nem határoz meg területet, akkor vannak olyan módszerek, amelyek lehetővé teszik a határon kívüli értékek értékelését.
Például a hőmérséklet-hiba a következő összefüggéssel függ össze a lineáris terjeszkedés együtthatójával (# 945;):
A hőmérsékleti hibák elkerülése végett a mérőeszköznek és a mérési objektumnak ugyanolyan normál hőmérsékletnek kell lennie, mint t0 = 20 ° C. Különösen pontos méréseket kell kondicionálni.
A reprezentáció formája szerint az abszolút () és relatív () hibákat különböztetjük meg:
A feldolgozás módszerével véletlenszerű és szisztematikus hibákat különböztetünk meg, az utóbbit korrekciókkal lehet megszüntetni.
Tekintsünk egy pontos dugattyút (példaértékű mérőeszköz) és egy hagyományos mérőműszert (működő mérőműszert) tartalmazó nyomásmérőket, amelyek ugyanolyan nyomással vannak terhelve - Px.
A méréseket több ponton, többször is elvégzik. Szerezd meg az alábbi hibákat # 916; x a mért értéken.
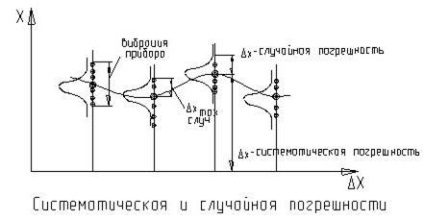
A hatótávolságon belül az üzemi nyomásmérő leolvasása több ponton történik, minden alkalommal, amikor a referencia mérőműszer újra be van töltve.
Az ugyanolyan nagyságú méréseket azonos körülmények között megismételjük.
A pontok az ismételt kísérletek eredményei, elég sokan lehetnek. A Gauss-eloszlás legalább 30 dimenzióban használható, különben a Student-tesztet használják.
Vegyük a Hobr-értéket, amely a példamutató mérési módot mutatja. A hiba nagysága a műszer és a modell olvasásának összehasonlításával érhető el:
A közvetlen mérési eredmények feldolgozásával meghatározzuk a fennmaradó elosztási paramétereket.
A mérés első statisztikai paramétere a matematikai elvárás:
Sok véletlen mérési hiba:
Átlagos négyzetes eltérés:
Ennek eredményeképpen bármely pont köré terjeszthetünk - a matematikai elvárásokat.
A matematikai elvárásnak a mérés tényleges értékétől való eltérése a hiba szisztematikus összetevője:
Az egyszeri ismételt mérések eltérése a matematikai várakozástól a véletlen eleme a hibának:
A véletlenszerű hibák elterjedését a matematikai elvárásokhoz képest a mérési eszközök változása jellemzi.
§ 27.8. A mérési eredmények feldolgozása. Egy és több mérés. A mérések bruttó és szisztematikus hibáinak elhárítása. A mérési hiba véletlen komponensének becslése.
- egy sor véletlenszerű mérési eredmény (ismételt kísérletek, amelyek közül a mérési hiba szisztematikus összetevője kizárt).
Használata képletű (27,12) van a matematikai elvárás egyenlet alkalmazásával (27,13) - több véletlen mérési hibák segítségével (27.14) - az átlagos négyzetes eltérés, és a hibákat ki vannak zárva:
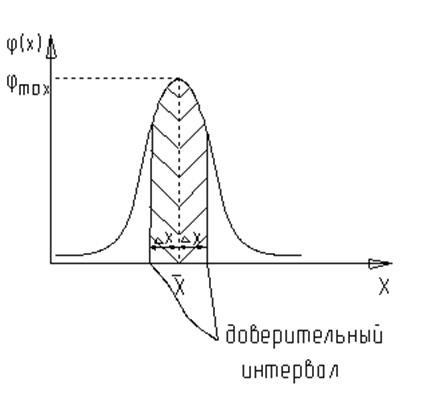
A grafikon az ismételt kísérletek eredményeit mutatja. Miután építése hisztogramok vagy matematikai feldolgozást alkalmazzuk a megfelelő Gauss-féle eloszlás görbe, a maximális, amely található egy megfelelő pontban az elvárással, formájában a görbe határozza meg két statikus paraméterek - átlagos és standard deviációját.
A görbe ismeretében bizonyos időközönként meg lehet állapítani a mérés előfordulásának valószínűségét, a többi dimenzióval ellentétben a matematikai várakozással szimmetrikus konfidenciaintervallum fogalmát hozza be, és viszonylagos bizalmát relatív értékkel határozzuk meg. A Gauss-függvény egyenlő, így meg lehet határozni az egyetlen mérés eredményének megjelenési valószínűségét a normál eloszlás kvantilis Laplace függvényének kétszerese között:
A technikai mérésekben a bizalmi érték általában 0,95, ami megfelel a normál eloszlás kettős kvantilusának:
Néha a szignifikáns tényezőt használják. egyenlő az egység és a bizalom közötti különbséggel
intervallum # 916; x ebben az esetben hívják - bizalom. és a valószínűség bizalmi valószínűség.
Tegyük fel, hogy 1000 mérést végeztünk el, 0,95 valószínűséget választunk ki, ezért egy adott x-ben meg kell határozni a hiányokat. Természetes, hogy a 950 mérés a konfidenciaintervallumon belül van, és 50 lehet a határértékeken kívül, azok a mérések, amelyek kívül esnek a konfidenciaintervallumon, természetesek a mérések számához. 100 mérésnél 95-nek kell beírnia az intervallumot, 10 mérés kívül, az egyik lehet az intervallumhatárok mellett, vagy semmi. Továbbá a mérések eltérnek a matematikai várakozástól, minél kisebb a valószínűsége a megjelenésnek, és annál nagyobb a valószínűsége, hogy ez a mérés hibás.
Annak érdekében, hogy a véletlenszerű változók egész sorából kimaradjon, válassza ki azt az eredményt, amelynek maximális eltérése a matematikai elvárástól. a kvantilis helye található. amely ha nem haladja meg az S (n) Chauvin kritériumot. a mérések számától függően az eredmény nem tekinthető hibásnak:
Ha a feltétel nem teljesül, a mérés eredménye megszűnik, és a feldolgozást új értékekkel ismételjük meg. amíg az összes hiba megszűnik. Ezután a mérési eredmény a következő formában van írva: