Tigrisek, ellenőrzés 1
[szerkesztés] Leírás
[szerkesztés] Elmélet
[szerkesztés] Nyeregpontok
Saddle pont mátrix - egy formális eleme a mátrix, vagyis az ő oszlopban, ez a legnagyobb (az egyik legnagyobb, hogy nem feltétlenül a>), és az ő sorban ő az egyik legkisebb. Például egy mátrixban
egy nyeregpont a második sor első oszlopának eleme, mivel> = az első oszlop minden más eleméből és <= всех остальных элементов второй строки. Довольно просто показать, что если у матрицы несколько седловых точек, то все их значения равны. Для поиска всех седловых точек в матрицах большой размерности не нужно рассматривать каждый элемент отдельно, можно воспользоваться алгоритмом, опирающимся на вспомогательную теорему. Работу алгоритма покажем на примере поиска всех седловых точек матрицы
Összegyűjtjük a legkisebb értékeket minden sorban, kapunk (-4, 2, 2, -3). Az összes oszlophoz (7, 2, 7, 2) a legnagyobb értékeket is összegyűjtjük. Ellenőrizzük, hogy az első sorozat legnagyobbja megegyezik-e a második sor legkisebb számával. Esetünkben ez így van, és ez a szám 2. Ha kiderült, hogy az első készlet maximális értéke kisebb, mint a második, akkor a nyeregpontok nem léteznének. És az a helyzet, hogy az első készlet maximális értéke nagyobb, mint a másodperc minimális értéke, külön bizonyítható. Tehát most nézzük meg, milyen pozíciók vannak 2-ki a mi készletünkben. Az első az. és a másodikban. Ezen készletek termékein minden nyeregpont található (azaz X = <. . .> )
De hol van a játékok elmélete? Az a tény, hogy amikor egy-egy játékot játszik, amikor a játékosok érdekei közvetlenül szembenézünk, akkor a stratégiák mátrixát és a nyeregpontok fogalmát használjuk. Például, amikor kő papír ollót játszik, a stratégiák mátrixa így néz ki
ahol a stratégia közvetlenül kiválaszt egy kőt, ollót vagy papírt, és a stratégiák kereszteződésében, az első játékos nyereménye. Az első játékos kiválasztja a sort, a második az oszlopot választja. Meg lehet győződni arról, hogy a mátrixnak nincs nyeregpontja. Csakúgy, mint az érdekes játékok szinte minden mátrixát. De képzeljük el, hogy a mátrix kicsit más lesz
És a stratégiák kereszteződésekénél az első játékos nyereménye rubelenként. Ez azt jelenti, hogy ha az első játékos kiválasztotta a papírt, és a második játékos választotta a papírt, akkor a második játékos az első 2 rubelt fizeti. És ha az első játékos az ollót választja, és a második kő, akkor az első játékos fizet a második 1 rubelt. Nyilvánvaló, hogy az első játékos azonnal megérti, hogy mindig papírt kell mutatni, azóta csak győzni fog. És a második, megpróbálva kevésbé veszít, megmutatja a kőből, mert kőből mutatkozik, elveszíti a rubelt, nem kettőt. Mint valószínűleg már kitalálta, a második oszlop első sorában a pont a nyereg (ellenőrizhető). A profitorientált játékosok stratégiákat választanak, hogy a nyeregpontok a kereszteződésüknél legyenek. És az érték ebben a pontban (ebben az esetben 1) nevezzük a játék értékét. A triót a játék döntése jelenti. A mi esetünkben ez (vagy mi ugyanaz a dolog).
De nagyon torzítottuk a stratégiák mátrixát, és így a szabályokat, a játék "kőpapír olló". Egy ritka személy szeretne részt venni benne, mint Player 2. A mi módosításaink tisztességtelenné tették a játékot. A nyeregpont jelenléte, mint általában, a játék igazságtalanságát jelzi
[szerkesztés] Vegyes stratégiák
Ha nincs nyeregpont, elindul a valószínűségek keresése, amellyel a stratégiákat el kell osztani a legnagyobb nyereség elérése érdekében. Vagyis már világos, hogy nincs "mágikus" stratégia az élet minden esete számára, és hogy különböző stratégiákat kell választanunk különböző valószínűségekkel

[szerkesztés] Mátrix játékok megoldásának módszerei
A grafikus algoritmus a második feladat megoldásának példáján látható a kontrollból.
Van egy módja annak is, hogy a nem-informatív húrokat és oszlopokat kidobjam a stratégiai mátrixból. Ehhez szükség van a gyenge domination és a konvex kombináció fogalmára:
- A vektor gyengén dominálja a b vektort. ha bármely i-edik elem a nagyobb vagy egyenlő az i-edik elemvel b.
- A konvex kombináció olyan vektorok lineáris kombinációja, amelyben az együtthatók nem negatívak és az összegben egységeket adnak. Például a 0,2a + 0,3b + 0,5c vektorok konvex kombinációja a. b és c
Szóval, akkor dobhatunk ki egy sztringet, ha létezik egy olyan domború kombináció a többi sorról, amely gyengén uralja ezt a sort. És csak akkor oszthatunk ki egy oszlopot, ha gyengén uralja a fennmaradó oszlopok konvex kombinációját.

[szerkesztés] Feladatok
[szerkesztés] Probléma 1
[szerkesztés] Pont a
Válaszoljon a kérdésre és indokolja, hogy az N xN mátrix pontosan (lekerekített) nyeregpontokkal rendelkezik-e?
- Egyenetlen N, igen, mivel ez pontosan a mátrixelemek fele. Töltsd be a bal felét nullákkal és a megfelelő értékekkel. Pontosan megkapjuk az elemek számát, mivel minden nullánk a legnagyobb az oszlopokban és a legkisebb a sorokban
- A páratlan N ott, mint módszer megtalálására nyereg pont alatt ismertetett elmélet alapja a tétel, a következménye, ami az, hogy több nyereg pontot képviseli, mint egy téglalap, vagyis a ponthalmaz [x, y] ahol x tartozik és X. Y Y. Azaz, tartozik a száma nyereg pontot kell bontani két tényező, amelyek mindegyike kisebb, vagy egyenlő, mint N. tehát a 3x3 mátrix lehet nyereg pont 7, például a 7 - prímszám. N = 25 = 313, de ez a szám nem osztható bármelyike szám 2 és 25
[hivatkozás szükséges] b. pont b
Válaszolj a kérdésre és indokold meg, hogy az N xN mátrixban nincs nyeregpont?
Igen, természetesen. És ez nem függ N (N> 1 esetén). példa
Minden 0 a legkisebb a sorában, de az oszlopban nem a legnagyobb.
Minden 1 az oszlopban a legnagyobb, de nem a legkisebb a sorában.
[szerkesztés] Mutasson be
Válaszoljon a kérdésre és indokolja, hogy az N xN mátrix pontosan egy nyeregponttal rendelkezik-e?
Igen, természetesen. És nem is függ N. példa
Az egyetlen nyeregpont itt 1 (könnyű ellenőrizni)
[szerkesztés] 2. feladat
Keresse meg a játék megoldását a stratégiai mátrixhoz
Megoldjuk az n = 25, de valójában kevés, hogy attól függ, N. Látjuk, hogy nincs nyereg pont, ami azt jelenti, van egy megoldás (ahol szükséges) csak a kevert stratégiák
A grafikus módszert használjuk, melyet 2xn és m x2 mátrixokra tervezünk
A mátrixunk három oszlopának együtthatóit használva a vonalak három egyenletét írjuk le
A metszéspontok kiszámításánál a grafikonokat (p értékek 0-tól 1-ig veszi fel)
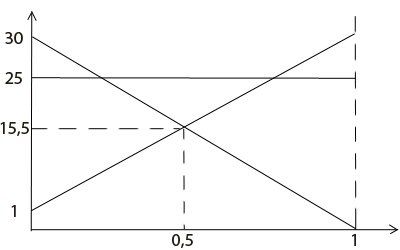
Az összes kereszteződések választani azokat, amelyek nem felelnek meg az egyéb közvetlen választani, amelyik balra. A mi esetünkben, minden egyszerű, ez a egyenes metszéspontja az L1 és L3. P-érték azon a ponton, 1/2, és így a forgalmazási stratégia az első játékos van P = p. 1-p> =. Az érték a játékban van 15,5 (érték L1 és L3 találkozásánál). Továbbra is megtalálja a második játékos terjesztési stratégiáját. Ehhez még egy egyenletet kell megoldanunk. Átmentünk vonalak L1 és L2, így veszi az első és a harmadik oszlop az eredeti mátrix. Mind a felső elem alsó kivonó (így megkapjuk az együtthatók az egyenlet a második játékos): K1 = 1 - 30 = -29, k3 = 30 - 1 = 29. azokkal helyettesíti Eq
most Q = q. 0, 1 -q> (azoknál a vonalaknál, amelyek nem vesznek részt a metszéspontban, beállítjuk a nulla valószínűséget), ezért Q =
Ui Még könnyebb megoldást találni. Ha N> 15, akkor ki tudja dobni a középső oszlopot, mert uralja az első és a harmadik oszlop összegének felét. Ezután kapunk egy ciklikus 2x2 mátrixot, amely grafikus módszer nélkül könnyen megoldható