A plazma tomográfiája - 1. rész, a szerző platformja
A monográfia a plazmaelemek tomográfiai diagnosztikájának modern módszereit mutatja be a kibocsátott vagy áthaladó fényhullám jellemzői alapján. Megrajzolják a számítógépes tomográfia matematikai alapjait, leírják azokat a megfelelő két- és háromdimenziós algoritmusokat, amelyek a plazma valós kísérleti tanulmányaiban találtak alkalmazást. A TO PAS alkalmazási programjainak rövid leírását a számítógépes gáz- és plazma tomográfia feladatokra fejlesztették ki. A diagnosztikai információk gyűjtésére szolgáló emissziós, interferometriás és árnyékképző rendszerekben működő plazma tomográfiai rendszerek szerkezeti jellemzőit jellemzik. A számítógépes tomográfia elméleti és kísérleti alapjainak megfelelő szakaszairól részletes bibliográfiát adunk.
A könyv a plazmafizika, az informatika, a számítástechnikai matematika, valamint a szakterületen dolgozó egyetemisták szakemberei számára készült.
IL. 122. Bibliograf. 540 név.
Ez a monográfia a plazma tomográfia diagnosztikájának modern problémájával foglalkozik. A plazmakoncentráció emissziós és átviteli adatainak értelmezésével foglalkozik. A számítógépes tomográfia matematikai hátterét két- és háromdimenziós algoritmusokkal együtt adják meg, amelyeket a plazma valós kísérleti vizsgálata során alkalmaztak.
A speciálisan a gáz- és plazma tomográfiára kifejlesztett "TOPAS" szoftvercsomag rövid leírása. A könyv a plazma tomográfiás rendszerek széles skálájának jellemzőit mutatja be, amelyeket a kibocsátás, az interferometriás és a schlieren típusú diagnosztikai beállítások számára fejlesztettek ki.
A könyvet akadémiai és ipari kutatóknak szánják, különösen az új területeket és a diákokat.
A SERIES PUBLIKÁCIÓS TANÁCSA
E. P. Volchkov, G.-N. B. Dandaron, BN kilencedik (felelős áll.), GA Dyuzhev, MF Zhukov (szerk.), V. V. Kudinov, Yu. V. Kurochkin, A.I. Leontiev, VP Lu-
kashov, HL Novikov, AA Ovsyannikov, IG Panev, VD Parkhomenko, LS Polak, NA Rubtsov, LM Sorokin, PI Tamkivi, BA Uryukov (főszerkesztő-helyettes), Yu. V. Tsvetkov, VS Engel'sht
A fizikai és matematikai tudományok doktora. Buchheim, AN. Papyrin
Elfogadta az Elméleti és Alkalmazott Mechanika Intézet SB RAS
Az olvasó számára felajánlott könyv egy kísérletet tesz a plazma tomográfia problémáinak megfontolására, amint azt a kísérletező és a teoretikus együttes álláspontjaiból látjuk.
A plazma diagnózis inverz problémáinak megoldása lehetetlen lenne a megfelelő matematikai berendezés nélkül, ezért a fizikai szigorúsági szinten belül a plazma tomográfia problémáinak megoldására szolgáló módszerek és algoritmusok egydimenziós vagy háromdimenziósak.
BEVEZETÉS A TOMOGRÁFIA MÓDSZEREIN
A közelmúltban a plazma kölcsönhatásai során felmerülő folyamatok, amelyek egymással és különböző típusú mágneses mezőkkel lépnek fel, jelentős érdeklődést mutatnak. Gyakran előfordul, hogy az interakció komplexitása miatt a plazmaképződés tengelyirányú szimmetriája zavart lesz. Ezért ezeknek a területeknek a plazma paraméterekre gyakorolt hatásának vizsgálata során szükségessé válik a tomográfiai vizsgálati módszerek alkalmazása.
Ez a fejezet bemutatja a számítógépes tomográfia (CT) alapelveit, valamint a plazma tomográfiás (PT) metódusainak azon tulajdonságait, amelyek lehetővé teszik a plazma objektumok lokális paramétereinek meghatározását nagyon korlátozott kísérleti adatokkal.
1.1. OPTIKAI MÓDSZEREK
A CT az alkalmazott tudomány területe, amely ötvözi a számítástechnikai matematika, a számítástechnika, a fizika és sok más modern tudományos trend eredményeit [485, 490, 534]. Tekintsük a kétdimenziós esetben a kibocsátási és abszorpciós plazma tomográfia legegyszerűbb problémájának általános megfogalmazását.
A sugárzás átviteli egyenlet az L vonal mentén van [514]
ahol e és x a helyi emissziós és ab szorpciós együtthatók egy fix frekvenciájú v; I az L vonal mentén lévő koordinátája. A kimenő sugárzás ezen egyenletének megoldása a következőképpen íródott:
(1.1.2) a következő eredményt kapjuk:
Integrált plazma sugárzás / „(£, p) (kiálló rész) mentén mérjük közvetlen sugarai a rendszer (ábra. 1.1) által meghatározott irányt £, és a r távolság eredetű 0 (néha sugarai integrációs beállítva a rendszerben (R, c), ahol a szög jellemzi a normális sugarak szöghelyzetét a sugárhoz, és néha a szokásos közvetlen referencia-rendszert is használjuk).
Ábra # 9632; 1.1. A plazma sugárzás tomográfiai regisztrálása.
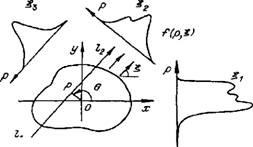
A közelítése opti-lag vékony plazma (n = 0) által leírt klasszikus sugárzás észleltünk NYM integráltranszformáció Ra-Dong [457] (a továbbiakban: neiz-Vestn helyi együtthatója kibocsátás együtthatóit
g (x, y), és a rögzített integrált sugárzást f0, t) jelöli:
Az 1. ábrán. Az 1.1. Ábra a vizsgált plazmaobjektum sík keresztmetszetét mutatja a g (x, y) helyi kibocsátási együtthatók eloszlásával. Miután megmértük az integrált sugárzást a diagnosztikai kísérletekben egy szögkészlethez, £ (0.180 °), és egy koordináták számára, megkaphatjuk a szükséges megoldás becslését:g = R'a \ f + V) - (1.1.4)
Itt az "1" az inverse radon transzformációhoz tartozó közelítés, és rj a vetítési adatok zajösszetevője.
E könyv következő fejezetei az egyenlet (1.1.3) inverziójának módszereire vonatkoznak különböző közelítésekben. Itt vázlatosan bemutatjuk a megoldás megszerzésének legfontosabb lehetőségét.
Bemutatunk egy forgást egy szög alatt koordinátarendszer (s, p): s = x cos | + Y sin |, p = - xsinJ + ycos |. (1.1.5)
Az elforgatott rendszerben g (s, p) g (s, p) függvényt fejeznek ki kétdimenziós Fourier transzformációjával (vs, vp):
g (s, p) = ff Kv ^ exp + pvp)] dvsdvp. (1.1.6) - 00
Most írjuk a g (s, p) függvény kirajzolásának kifejezését az s irányba:
1) = fg (s, p) ds = f / g (vs, v \ dv3dvj ds exp [A (n> n + pv)
- / / exp [Oji (pvp) \ g (vslvp) 6 (vs) = advsdvp = -00
= Ay Ayaplfiltr ^ p ti (yt, v) I = 0. (1.1.7)
Könnyű látni, hogy a kivetítés kifejezése keresztül
inverz Fourier-transzformáció a Fourier transzformáltja kívánt tomogramok g (vs, vp), a középső szakasz hozott vs = 0. Ebből közvetlenül követi az úgynevezett központi szelet tétel, amely összeköti a egydimenziós Fourier transzformáltja vetületét kétdimenziós Fourier - módon megoldások:
Az (1.1.6) egyenletet átírjuk a poláris koordinátarendszerben:
= f dJ f g (v, ψ) exp [fbrvr sin (
Itt (r,
Végül van egy olyan formula, amelyet inverz radon transzformációnak nevezünk:
ahol p0 = - xsin | + ycos | = rsin (
Széles körben ismert az orvosi tomográfia sikere, amely lehetővé teszi az orvos számára, hogy megfigyelje a beteg különböző szerveinek szerkezetét a képernyőn, diagnosztizálja betegségét. Mi a plazma tomográfia (PT) feladatainak sajátossága, különbsége az orvosi CT feladataitól? Nézzük meg azokat a PT-feladatok jellemzőit, amelyek megnehezítik azok megoldását:
- a megfigyelések kis számú iránya (előrelépések) K \
- kisszámú számlálás (p-rel szemben) N \
- szögkorlátozások az előrejelzések nyilvántartásában;
- az előrejelzések lehetséges eltérése;
- a jel-torzító hardverfunkciók széles körének jelenléte a detektáló rendszerekben;
- a mérési csatornák különböző statisztikájú zaj jelenlétét;
- bizonyos esetekben a plazmaobjektumok átlátszatlan zárványainak megjelenése;
- a sugaras pályák lehetséges eltérése a rectilinearis pályától a refrakció miatt.
A vetületi adatok PT-ben történő mérésére szolgáló módszerek általában a plazma diagnosztikai információinak megszerzésére szolgáló klasszikus módszerek továbbfejlesztése. Alapvetően ez a kibocsátási (különböző spektrális tartományban - infravöröstől lágy X-th) Hajtómű: interferométer (szintén a különböző területeken Meas-elektromágneses hullámok) deflektometricheskie (szemcsekép, Schlieren és árnyék), stb A korpuszkuláris és módszerek .. [422, 434, 501, 506, 507, 532]. Mindegyikük természetesen elsõsorban egyszögmérõ rendszerekhez készült. Bizonyos korlátozások az osztály a vizsgált plazma formáció még az ilyen adatgyűjtő rendszereket lehet tulajdonítani a tomográfia, ha azok lehetővé teszik a mért adatok alapján határozza meg a helyi plazma jellemzőit több szakasza, és néha az egész kötetet.
Az egyszög tomográfia változatai olyan problémákat jelentenek, amelyekben ismert a helyi emissziós együtthatók izolátuma (vagy isosaurusz). A leghíresebb ilyen példa az axiális (vagy hengeres) szimmetria. Ezután az izolinok koncentrikus körök, és az egyedi f (p) vetület kapcsolódik a kívánt g (r) megoldáshoz az integrál Abel-egyenlettel:
a plazma plazmamagnosztikája a JI-2 stellarátoron [370, 408], valamint az ívplazma diagnózisában [442].
Hangsúlyozni kell, hogy a Ref. [484] -ben kifejlesztett rekonstrukciós elmélet (egy korábbi cikk [466] alapján) lehetővé teszi egy lövéses tomográfia mind a ventilátor, mind a párhuzamos rögzítési rendszerekben. A [260] orientált diagnózis tokamak ASDEX, különösen kapott eredményeket a kontúr-cal ellipszis alakú (kontúr koaxiális, a = p = 0 (1.1.13)) a ventilátor nyilvántartási rendszerben.
Vannak olyan plazma berendezések, amelyeknél a mágneses fluxus kiszámítása "azt sugallja, hogy létezik egy háromszögletű izolinrendszer a helyi kibocsátási tényezők számára. Ezek közé tartozik a tróna törzs, és különösen a különböző üzemmódokat torsatron Hurricane-3 [328] értelmezése odnorakursnyh fan leírt dimenziók egyszerű algoritmusokat háromféle kontúrok rendszerek [487, 489, 490]. Az egyszög tomográfia legáltalánosabb esetét a [487, 489] írja le. Itt, az információt a forma körvonalait a kívánt kibocsátási faktort lehet definiálni, mint néhány más funkciót a két változó (x, y), gyakran nevezik a táblázatot [V ^. Az ilyen funkciók egy példája a mágneses egyensúlyi egyensúlyban levő mágneses fluxus eloszlások.