A lineáris automatikus vezérlőrendszerek elemeinek egyenletessége és átviteli funkciói
Az automatikus vezérlés bármely rendszere meglehetősen bonyolult lehet, és több elemből áll, amelyek különböző kapcsolatokkal vannak összekapcsolva. A vezérlő objektum lehet több objektum összekapcsolása, és a vezérlőnek más elemei is lehetnek, kivéve a korábban megfontolt alapokat. Ezután a vezérlőrendszer szerkezeti rajza alakulhat ki
A rendszerben található hivatkozások lehetnek: alap, kiegészítő, kiegészítő inverz.
A fő kapcsolatot a fő befolyási lánc alkotja (a rendszer fő átjárója). Például: mob - 1 - 2 - 3 - # 966; - az objektumhoz; # 966; → 4 - 5 - 6 - 7 - mreg - a vezérlőhöz.
További kommunikáció - a főbbeken kívül a hatások átvitelének módját képezi. Például: a 9. elem, amely párhuzamosan helyezkedik el a 6 elemhez.
A további visszacsatolás egy elem kimenetére irányul a bemenetére vagy az előző elemek bemenetére. Például: a 8 elem a 7 elem kimenetétől az 5 elem bemenetéhez tartozó jelnél.
Elemek szerepelnek a vezérlőrendszer legyen egyszerű, vagyis át a jelet a bemenettől a kimenetig, és annak viselkedését időben leírható egy differenciálegyenlet nem magasabb, mint a második sorrendben, amelyek kialakulhatnak mindig is a fizika a folyamat.
Mivel egy komplex vezérlőrendszer differenciálegyenletét szinte lehetetlen fordítani, a következő megközelítést használják az automatizálásban:
1) fel kell szakítani a rendszert egyszerű elemekké;
2) megkapják az elemek differenciálegyenletét;
3) differenciálegyenletük segítségével átvitelük funkciójukat;
4) figyelembe véve az elemek kapcsolódását a vezérlőrendszerben, a rendszer átviteli függvénye az elemek átviteli függvényéből származik;
5) a rendszer differenciálegyenletét a rendszer átviteli függvényéből kapjuk meg.
Tegyük a tartály differenciálegyenletét vízzel vízszint-szabályozó objektumként. Ez a szabályozási rendszer egyik eleme (13.
Ábra. 13. Q1. m 3 / s - vízbeáramlás; Q2. m 3 / s - a tartályból folyó víz; S - tartály rész, = const, m2; H0 a statikus érték szintje; DH = H - H0 - a szint eltérése a statikus (meghatározott) értéktől; V0 - a folyadék térfogata a tartályban statikus üzemmódban; DV - dinamikus üzemmódban változtassa meg a folyadék térfogatát.
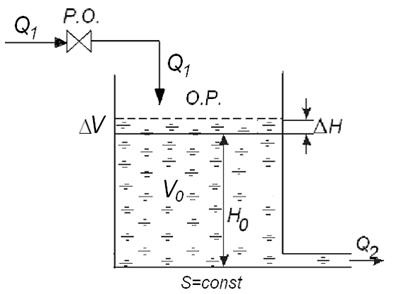
- a dinamika egyensúlyi egyenlete
Tüntesse fel a költségeket eltérésekben:
(a statikus rendszer egyenletéből).
Az ábrából következik, hogy a H szint nem befolyásolja a Q1 beáramlását. A H-szint a Q2 tartály vízmennyiségét befolyásolja. következésképpen Q2 a szint függvénye. Az automatikus vezérlőrendszerek elméletében a paraméterek kis mértékű eltéréseit (H szint) egy adott értéktől (H0) tekintjük. Ebben az esetben feltételezhető, hogy a kimeneti mennyiségek a bemeneti mennyiségek változásával arányosan változnak. Ebből kiindulva le lehet írni
ahol k n - arányossági tényező (nyereség).
Ezután a tartálydinamika egyenlet lesz
A (6.1) egyenletet a formában írjuk
Bevezetjük a jelölést :; és írja le a (6.2) egyenletet ezt a jelölést használva
Ebben az egyenletben K a dimenziós nyereségtényező. A kimeneti mennyiség (DH) aránya a bemeneti mennyiség (DQ1) dimenziójához tartozik. A T [c] derivált együtthatója az idő dimenzióját jelenti, és az időállandónak nevezzük. Ez egy lineáris differenciálegyenlet.
Összeállításában differenciálegyenlet bármely más elem ellenőrző rendszerek, amelyekben más fizikai folyamatok zajlanak (például, a fűtés kemence), az expressziós kiszámítására az R és T tartalmazni fogja más fizikai mennyiségek, de a forma az egyenlet lehet ugyanaz.
Az automatizálás során leggyakrabban az egyenleteket dimenzió nélküli formában kezelik. Ezután ugyanazok az elemek, amelyekben teljesen más fizikai folyamatok vannak, de ugyanolyan típusú differenciálegyenletek, az automatizálás szempontjából.
Az elem differenciálegyenletének dimenzió nélküli formája.
Ha az egyenletet dimenzió nélküli formában írjuk, válasszuk ki az egyenletbe belépő mennyiségek alapértékét. Az alapérték a beállított paraméterérték (H0) és a maximális beáramlások (költségek) lehetséges változása.
Bevezetjük a szint (# 966;) és az áramlási sebesség dimenzió nélküli értékeit a mellékfolyóba (# 956;)
Ezután a tartálydinamika egyenlet lesz
Ezután az egyenletet az automatikus vezérlés elméletében általánosan elfogadott formában írjuk
Ebben az egyenletben T. [c] az idő dimenziója, ezért időállandónak nevezzük. és k a dimenzió nélküli elem nyereség (átviteli együttható).
A statika egyenletének formája lesz. ahonnan a k erősítés azt jelzi, hogy a kimenet hányszor nagyobb vagy kisebb, mint a bemeneti érték statikus üzemmódokban.
Lehetőség van a két sorozatban összekapcsolt tartály differenciálegyenletének vízzel való kialakítására. Ezután megkapjuk a forma másodrendű differenciálegyenletét
Ebben az egyenletben a származékok koefficienseinek időbeli dimenziója van, ezért T1 és T2 időállandó.
Bonyolultabb elemekben bonyolultabb differenciálegyenleteket lehet beszerezni, pl.
Mivel a munka a jövőben differenciálegyenletek elég kényelmetlen és nehézkes a automatizálási paraméterek időtől függően t, át a sík komplex számok bevezetése a különböző szereplők számára. E számok síkjában olyan algebrai egyenleteket kapunk, amelyek sokkal könnyebb dolgozni. Ha a differenciálegyenleteket más paraméterek síkjába fordítjuk, a Laplace transzformációt alkalmazzuk, de gyakrabban formális fordítást vezetünk be a differenciálódási operátor bevezetésével.
Írjon egyenleteket a kezelői formában.
Használja hivatalos átutalási differenciálegyenletek szereplő formában, amely teljesen egybeesik szigorú alkalmazásával Laplace-transzformáció, a nulla kezdeti feltételek, ami gyakorlatilag mindig történik a lineáris szabályozási elmélet.
Bemutatjuk a differenciálást végző operátort:
Itt p a differenciálási operátor. Ezután a kezelői formában a korábban írt differenciálegyenletek a következő formában lesznek:
Ezek az egyenletek algebraiak. Számukra egy algebra tulajdonságait alkalmazhatjuk például, hogy konstans tényezőt alkossunk # 966; és # 956; a zárójelben. A fenti egyenleteket a következő formában kapjuk meg.
Ezek az egyenletek általános formában írhatók:
ahol D (p) a függvény sajátfunkciójának nevezzük # 966; és k (p) a hatások kezelője # 956;.
Ezután a fenti egyenleteknél (6.12) a sajátvektorok és a műveletek kezelői a következők:
Bevezetjük egy átviteli függvény fogalmát:
Szigorú meghatározás. A W (p) átviteli függvény a kimeneti mennyiség Laplace képének aránya # P (p) az m (p) bemeneti mennyiség Laplace képére zéró kezdeti feltételek mellett
Az egyenlet általános képletben (6.13) való jelzéséből következik
Tól (6,17), ebből következik, hogy a megtalálja a kimeneti érték j (p) egy előre meghatározott művelet bemenet m (p) elegendő ahhoz, hogy tudjuk, az átviteli függvény W (p) az elem vagy a rendszer.
Az átviteli függvény második meghatározása
Az átviteli függvény a K (p) műveletek operátorának arányát és a D (p) függvény sajátfunkcióját jelenti, amely a differenciálegyenletek kezelői formában történő írásából származik.
Az egyes elemek átviteli funkcióinak ismerete lehetővé teszi a különféle elemcsatlakozások és az átviteli függvény átviteli funkcióinak megszerzését.
Különböző elemcsatlakozások átviteli funkciója.
Három fő kapcsolattípus létezik: soros, párhuzamos és soros kapcsolat visszacsatolással.
1. Transzfer funkció soros összekötő elemekben
Ábra. 14. Az elemek egymás utáni csatlakoztatása
Az átviteli függvény definíciójából következik, hogy e kapcsolat átviteli függvénye
Ebből következik
Ezután a kapcsolat átviteli funkciója lesz
Következésképpen az elemek soros összekapcsolásának átviteli függvénye megegyezik az összes elem átviteli funkcióinak eredményével.
2. Az elemek párhuzamos csatlakoztatásának átviteli funkciója.
Ha az elemek párhuzamosan vannak csatlakoztatva, ugyanazt a bemeneti jelet kapják, és a kimeneti jeleket összegzik (15. ábra).
Ezért az elemek párhuzamos csatlakoztatásának átviteli függvénye megegyezik az összes elem átviteli funkcióinak összegével.
Ábra. 15. Elemek párhuzamos csatlakoztatása
3. A soros kapcsolat átviteli funkciója visszacsatolással.
Vannak kapcsolatok az egyszemélyes és nem egységes visszajelzésekkel.
Kapcsolat egyetlen visszajelzéssel.
Ábra. 16. Az elemek szekvenciális összekapcsolása egyetlen visszacsatolással
Az egység visszajelzéseinek átviteli funkciója
A visszajelzések pozitívak és negatívak lehetnek.
Pozitív - erősíti a fő bemeneti jelet: xvx + xv
Negatív - gyengíti a fő bemeneti jelet: хвх - хвых.
Ahhoz, hogy az átviteli függvényt E vegyület razorvom visszajelzést és annak hatása a nyílt jelet fogja venni annak igazgatási rendszer bemenetére az első elem (x € X ± hvyh). Három elemből álló soros kapcsolatot kapunk, amelynek átviteli funkciója ismert - az átviteli funkciók terméke. Definíció szerint a zárt rendszer átviteli függvénye
Nyitott hurok átviteli funkció
Innen egy zárt rendszer átviteli funkcióját szerezhetjük meg:
A nevezőben lévő "-" jel (6.20) azt jelzi, hogy a rendszerben pozitív visszajelzést használnak. A bemeneti jel növekedésével az xv növekszik, ami ellentmond a szabályozási folyamat jelentésének. Ezért szabályozási célokra a pozitív visszacsatolás nem megfelelő. Ezt elsősorban különféle bemeneti jelerősítőknél használják.
A "+" jel a nevezőben (6.20) azt jelzi, hogy negatív visszajelzést használnak a rendszerben. A bemeneti jel növelésével az xv csökken. Következésképpen a szabályozási rendszerekben negatív visszacsatolást alkalmaznak. Ezután a rendszer átviteli funkciója lesz a formában
Csatlakozás nem egységes visszacsatolással (16. ábra)
Ábra. 17. Az elemek szekvenciális összekapcsolása nem egység visszajelzéssel
A visszacsatolás funkció átvitele definíció szerint
Ha megnyitja a rendszert, akkor az 1. elem bemeneténél jel lesz. Miután ugyanazt a dolgot végeztük el, mint egy visszacsatolás, egy zárt rendszer átviteli függvényét kapjuk negatív visszacsatolással a formában
Értékeljük a visszacsatolás hatását az xv rendszer kimeneti mennyiségének változására, amikor a xxx bemeneti változó változik. figyelembe véve a három elem (6.18) nyitott rendszerét és a zárt egység visszacsatolást (6.21) és a nem egységet (6.22).
Hagyja, hogy a rendszer elemei a legegyszerűbbek legyenek, és az átviteli függvények megegyeznek az amplifikációs tényezőkkel :; ; ; . Ezután a nyitott rendszerben (14. ábra) a kimeneti érték egyenlő lesz. vagyis az xv változása az xBx-ben jelentősen változik K-szeresben ().
Egy zárt rendszerben, egyetlen visszajelzéssel
azaz az xv változatlanul változik az xvx változásával összehasonlítva.
Zárt rendszerű, nem egységes visszajelzéssel ()
A visszacsatolás rendszerre (k4) gyakorolt hatás megváltoztatása széles tartományon keresztül lehetséges az xv kimeneti mennyiség változásának befolyásolása a k1 állandó értékeknél; k2; k3.
Tekintsük az automatikus vezérlõ rendszert (ATS) a szabályozási tárgy és a szabályozó aggregátumaként (18. ábra) a szabályozó befolyási csatorna mreg
Ábra. 18. Automatikus vezérlőrendszer
A zárt vezérlési rendszer (6.22.) Alapján az átviteli függvény leírása lehetséges
Mivel a vezérlő objektum jól definiált Wob (p) átviteli függvényt tartalmaz, amely gyakorlatilag lehetetlen megváltoztatni, a szabályozó viselkedését csak a szabályozó tulajdonságainak megváltoztatásával lehet megváltoztatni (a Vper (p) értékek megváltoztatásával).
Egy komplex rendszer átviteli funkciója.
Komplex rendszerekben különböző elemek kapcsolata lehet. Egy komplex rendszer átviteli függvényének meghatározásához a különböző vegyületekkel rendelkező régiókat azonosítják benne. A kapcsolatok átviteli funkcióinak képletei alapján megtalálják az átviteli funkciókat, és a rendszert ismert formába állítják - egy soros kapcsolatot visszajelzéssel.
Ábra. 20. Összekötő elemek összetett rendszere
Feltételezzük, hogy a W1 ... W15 transzfer funkciók ismertek. Tüntessük fel ebben a rendszerben az összetett vegyületeket: I, II és III.
Határozza meg a vegyületek transzfer funkcióit: WI. WII; WIII.
I - párhuzamos összekötése két lánc elem: 3 - 4 és 7 - 8
II - kapcsolat a visszacsatolással, amely tartalmazza a 14 elemet
III - a 12. és 15. elemek párhuzamos csatlakoztatása
A visszacsatolással rendelkező elemek egymást követő összekapcsolását kapjuk, amely magában foglalja.
Egy komplex rendszer átviteli funkciója lesz
hol van az elemek közvetlen összekapcsolásának átviteli függvénye? a visszacsatolás átviteli függvénye.