Chinmay chandrakar, kowar m
Átutalás: Tkachenko S.V.
Forrás: Open System Resuorces Online
Kivonat:
Az egyik fő probléma az EKG, a orvosbiológiai adatfeldolgozás elválasztani a kívánt jel által okozott interferencia távvezeték zavaró külső elektromágneses mezők, és alkalmi testmozgások a légzés. Jelenleg különböző típusú digitális szűrőket használnak a nemkívánatos frekvenciasávok jelének törléséhez. Az orvosbiológiai jelek interferenciájának csökkentése érdekében azonban nehéz rögzített együtthatókkal ellátott szűrőket alkalmazni, mivel az emberi viselkedés nem lehet pontosan előre jelezni. Az adaptív szűrés a technika, amely a probléma megoldásához szükséges. Ez a cikk előírja többféle adaptív szűrők zajcsökkentést az EKG jelek, például PLI és szűrés interferenciát az alapvonaltól. A MATLAB szűrők működésének modellezésének eredményeit bemutatjuk. Ez a cikk a rekurzív legkisebb négyzetek módszerét (RLS) használja. Az RLS algoritmust a jelek kis frekvenciájú komponenseinek eltávolítására használják. A legkisebb négyzetek algoritmust úgy tervezték, hogy minimalizálja a hasznos jel és a kimeneti szűrő modell közötti különbség négyzetének összegét. Amikor új mintát a beviteli jeleket mindegyik ismétlésnél, hogy megoldást találjanak a legkisebb négyzetek lehet számítani rekurzív formában eredményeként a rekurzív hívás legkisebb négyzetek algoritmust (RLS). Az RLS algoritmusokról ismert, hogy gyors konvergenciát mutatnak még azokban az esetekben is, amikor a bemeneti jel korrelációs mátrixának értékei nagyok. Ezek az algoritmusok kiváló teljesítményt nyújtanak, ha nem helyhez kötött állapotban dolgoznak. Mindezen előnyök elkerülhetetlenül kíséri növekedése számítási komplexitás és stabilitási problémák, de ezek a problémák nem kritikus a algoritmusok alapján LMS.
Kulcsszavak: EKG jel, Dirichlet feltételek, adaptív szűrő.
1. BEVEZETÉS
A háttérzajjal szennyezett nagy felbontású EKG-jelek eltávolítása fontos kérdés a kutatásban. E vizsgálatok célja az EKG-jel javítása. Az EKG pontos értelmezésének megkönnyítése érdekében el kell különíteni a megengedett jelösszetevőket a nemkívánatos mellékhatásoktól. Számos megközelítést írtak le az irodalomban az EKG adaptív szűrők alkalmazásával történő javítására [1] - [3]. Az ilyen szűrők lehetővé teszik a különböző idő-potenciálok érzékelését és a jelek dinamikus változását. A [4] - [6] -ben egy LMS-en alapuló adaptív szűrőt javasoltak a normál QRS komplexek impulzusválaszának periodikus vételére. Ezt a szűrőt ezután arra használják, hogy észleljék az aritmiákat a járóbeteg-EKG rekordokban. Az LMS algoritmus bemenetei determinisztikus függvények, és periodikus kiterjesztések határozzák meg, amelyek viszont ortonormális alapfunkciók csonkolt sorozata.
Ezekben az iratokban az LMS algoritmus egy azonnali alapon működik, például a vektor súlya, amelyet minden egyes új minta esetében aktualizálnak, egy azonnali gradiens becslés alapján. Vannak olyan klinikai EKG-jelfeldolgozó alkalmazások, amelyek nagyszámú indítással rendelkező adaptív szűrőket igényelnek. Ilyen esetekben a szokásos LMS algoritmus elfogadhatatlan, mivel a számítási erőforrásokra nagy igények vannak. Az LMS algoritmus és az NLMS (normalizált LMS) algoritmusok több számítást igényelnek, ezért széles körben használják az akusztikus visszhang-szupresszorokat. Az RLS (rekurzív legkisebb négyzetek algoritmusa) algoritmus, amelynek konvergenciája nem függ a bemeneti jeltől, a leggyorsabb az összes hagyományos adaptív algoritmus közül. Az RLS algoritmus fő hátránya a nagy számítási költségek. Mindazonáltal a közelmúltban gyors RLS algoritmusokat fejlesztettek ki. Ebben a cikkben gyorsabb algoritmust szeretnénk kapni, beleértve az impulzusszám ismeretét az RLS algoritmusban. Az NLMS és más projekciós algoritmusokkal ellentétben az RLS algoritmus nem rendelkezik skaláris lépésmérettel. Így az EKG-jel jellemzőinek változása nem tükröződik közvetlenül az RLS algoritmusban. Az RLS algoritmust az adaptív szűrők szempontjából vizsgáljuk, mert (a) az RLS algoritmust az adaptív szűrő speciális változatának tekintjük, és (b) az adaptív szűrő minden paraméterének fizikai jelentése van. A számítógépes modellezés azt mutatja, hogy ez az algoritmus kétszer olyan gyors, mint a szokásos algoritmus. Ez fontos szerepet játszhat a biotelemetriában, ahol az effektív diagnózis és a nagy adatsebesség közötti interferenciamentes EKG-jel eltávolítása szükséges az impulzusok megkettőzésének és a bizonytalanságok feloldásának elkerülése érdekében. Amennyire tudjuk, a domén-transzformáció nem tekinthető korábban az EKG-jelek interferencia jelének szűrésében. Ebben a cikkben bemutatjuk az RLS algoritmust az EKG interferenciájának eltávolítására. Ez az algoritmus kevesebb számítási komplexitást és jó szűrési képességeket kínál. A javasolt algoritmus hatékonyságának tanulmányozása érdekében az EKG-jel interferenciájának hatékony eltávolítása érdekében egy MIT-BIH adatbázis felhasználásával végzett szimulációt végeztünk különböző interferenciákra.
2. ALAPELV: NÉGYSZERŰ SOROZAT
A Dirichlet-feltételeket kielégítő időszakos funkciók skálázható szinusz- vagy koszinusz-értékek sorozata a gyakoriságnak az alapfrekvencia többszörös rezgésének frekvenciájára való tekintettel.
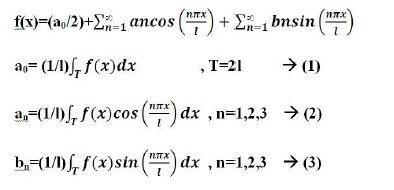
Az EKG jel periodikus, frekvenciája megegyezik a szívveréssel. A Dirichlet feltételeit is kielégíti:
Amint az az 1. ábrán látható, egy EKG jelidőszak egy háromszög és egy szinuszos hullámforma keveréke. Az EKG-jel mindegyik fontos jellemzője az oszcillogramok egyikének eltolt és skálázott változata lehet, az alábbiak szerint.
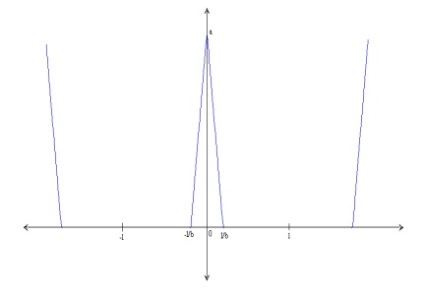
Ábra. 1. A QRS oszcillogram
Az (1) kifejezésből:

Az EKG-jel időszakos p-hullám részeinek generálása:
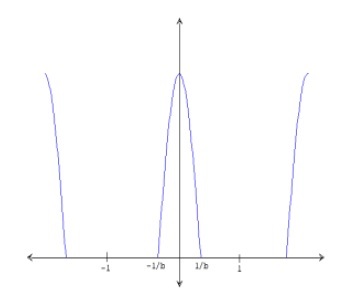
Ábra. 2. A jel p-hullámrészének oszcillogramja

4. INTERFERENCIA
Az interferenciával kombinálva a jel a kompenzátor "fő bemenetére" kerül. A második érzékelő megkapja az n1 interferenciát, amely nem korrelál a jelrel, de korrelál valamilyen ismeretlen útvonalhoz n0 interferenciával. Ez az érzékelő "bemeneti arányt" biztosít a kompenzátorban. Az n1 interferenciát szûrjük az "y" kimenet elõállítására, amely n0 szoros másolata. Ezt a kimenetet kivonjuk az "s + n0" fő bemenetből az s + n0-y kimenet létrehozásához. Ha ismeri azon csatornák jellemzőit, amelyeken keresztül interferenciát továbbítanak az elsődleges és a másodlagos érzékelőkhöz, létrehozhat egy fix szűrőt az n1 és y = n0 változások összehasonlításához. Ezután a szűrő kimenet kivonható a fő bemenetből, és a rendszer kimenete egyetlen jelet tartalmaz. Mivel azonban az átviteli útvonal jellemzői ismeretlenek vagy csak megközelítőleg ismertek, nem lehetséges rögzített szűrő használata. Sőt, még ha rögzített szűrő használata is lehetséges, annak jellemzőit nehezen elérhető pontossággal kell korrigálni, és a legkisebb hiba nagyobb interferenciához vezethet. A 2. ábrán látható rendszerben A 3. ábrán a másodlagos bemenet egy adaptív szűrővel van feldolgozva, amely a legkisebb négyzetek módszerével automatikusan beállítja impulzusválaszát. Az ilyen RLS algoritmusok a szűrő kimenetén a hibajel nagyságára reagálnak. A zajcsillapító rendszerekben a gyakorlati cél olyan s + n0-y rendszer kimeneti rendszer létrehozása, amely leginkább megfelel az s jelnek, figyelembe véve a legkisebb négyzetek módszert. Ezt a célt úgy érik el, hogy a rendszer kimenetét adaptív szűrő és szűrő beállítások segítségével adaptív algoritmus segítségével táplálják, hogy minimalizálják a teljes rendszer teljesítményét. Más szavakkal, az adaptív interferencia-elnyomó rendszerekben a rendszer kimenetét az adaptív folyamat jelzési hibájaként használják.
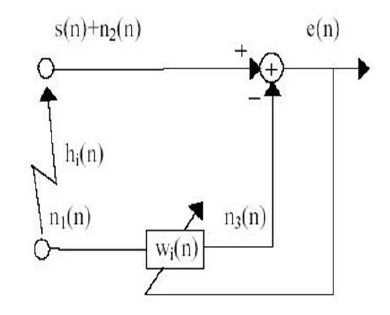
Ábra. 3. Adaptív zavarszűrő
5. RLS ALGORITHM
Az algoritmus célja az adaptív szűrő együtthatóinak kiválasztása oly módon, hogy az y (k) kimeneti jel a megfigyelési időszak alatt a hasznos jelnek felel meg, amennyire csak lehetséges a legkisebb négyzetek értelemben. A minimalizálási folyamat megkívánja a bemeneti jel rendelkezésre bocsátására vonatkozó információkat az előző időben. Ráadásul az objektív függvény, amelyre minimálisra törekszünk, determinisztikus. Az általános FIR adaptív szűrőt a 3. ábrán közvetlen formában hajtjuk végre. 3. A bemeneti jel információi jelenleg a k vektorban vannak.
az inverz determinisztikus korrelációs mátrix a következő formában számítható ki:
A teljes RLS algoritmust az 5.1 algoritmus írja le.

6. A MODELING EREDMÉNYEI
Annak bizonyítására, hogy az RLS algoritmus valóban hatékony klinikai helyzetekben, ezt a módszert több EKG rekord felhasználásával tesztelték, a hullám morfológiák széles skálájával a MIT-BIH arrhythmia adatbázisból. Munkánkban különböző frekvenciák interferenciájával szennyezett EKG-jeleket használtunk, amelyeket 200 csatornánként másodpercenként digitalizáltunk minden csatornán, 20 mV tartományban. Azonban valódi interferencia érhető el a normál sinus ritmus adatbázisból (NSTDB).
A. Az áramellátás interferenciájának adaptív szűrése
Az elektromos vezetékre való interferencia súlyos károkat okozhat az orvosbiológiai nyilvántartásokban. Javított adaptív kompenzátorral kínáljuk az átviteli vonal fő összetevőjének és az elektrokardiogramon (EKG) történő harmonikus interferenciát. A módszer 4 Hz-es frekvenciákon figyelemmel kíséri az összes vezeték interferenciájának amplitúdóját, fázisát és frekvenciáját. A tisztított jelet az összes módszer alkalmazása után az eredeti EKG-jelhez hasonlítjuk. Javított alkalmazkodó kompenzátorunk azt mutatja, hogy a fő komponensekhez viszonyítva a közvetlen interferencia zóna ereje akár 30 dB-rel magasabb, mint más módszerekkel. Ráadásul a módszerünk hatékonyan hat a hálózati vonal interferenciáinak összehangolására. A teljesítményinterferencia (PLI) kimutatására 50 Hz szinusz hullám szimulációt választottunk.
B. Alapvető vándorlás
A szennyezett EKG-jelet az 1. ábra szerinti adaptív szűrő fő bemenetére tápláljuk. 3.
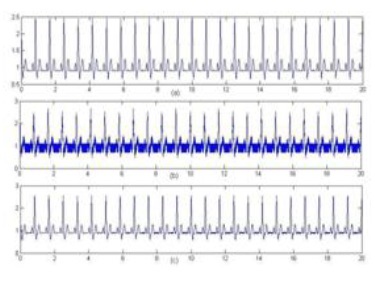
Ábra. 4. a) Tiszta EKG jel, b) EKG PLI interferenciával, c) RLS szűrt algoritmus.
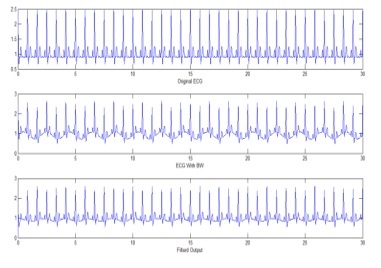
Ábra. 5. a) tiszta EKG jel, b) EKG BW interferenciával, c) RLS szűrt algoritmus.
C. Az izomzaj adaptív szűrése.
A nem-stacionárius interferencia jelenlétében végzett szűrés hatékonyságának bemutatásához az izomzajt (MA) az MIT-BIH adatbázisból vettük. Az EKG-k gyakran elektrofiziológiai potenciállal szennyezhetők, amelyek az emberi izmok összehúzódásával kapcsolatosak. Az ilyen izomtermékek bonyolítják az EKG értelmezését, vagy akár lehetetlenné teszik. Az ilyen interferencia eltávolításához az aluláteresztő szűrőket használják. Az izomzavarok frekvenciaspektruma azonban átfedhet az agyi jelek gyakoriságával. Így a szűrők elnyomják nemcsak az izmokat, hanem értékes információkat is.
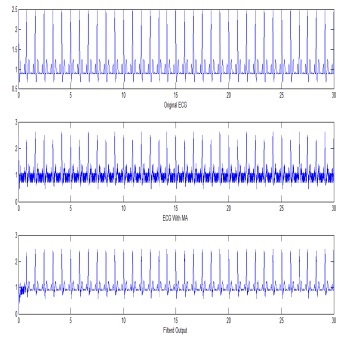
Ábra. 6. a) tiszta EKG jel, b) EKG MA-interferenciával, c) RLS szűrt algoritmus
D. Adaptív elektródák eltávolítása
Ennek bemutatásához tiszta EKG jelet használunk az elektródákból, EM-behatások hozzáadásával. Az EM interferenciát 15 Hz feletti frekvencián generálják. Az EM interferenciával szennyezett EKG jelet az adaptív szűrő bemenetére táplálják. Az EM-interferenciát referencia jelként használják. A szűrő kimenetén megkapjuk az előírt EKG jel nagy felbontását. Az eredményeket az 1. ábrán mutatjuk be. 7.
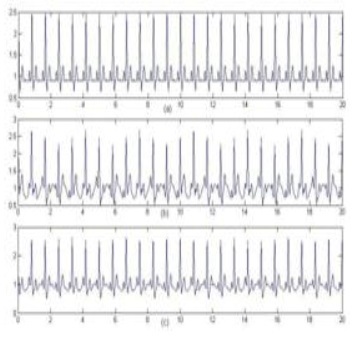
Ábra. 7. a) tiszta EKG jel, b) EKG EM zavarással, c) RLS szűrt algoritmus.
Ebben a cikkben bemutatunk egy eljárást az EKG-jel interferenciájának eltávolítására az RLS adaptív szűrő használatával. Ehhez a bemenetet és a hasznos jeleket úgy választják ki, hogy a kimeneti szűrő az eredeti EKG-jel legjobb minimális négyzetes becslését adja ki. A javasolt módszer a súlycsökkentési képlet változásait veszi figyelembe, és ezért a megfelelő LMS-alapú implementációkhoz képest növeli a sebességet. Tanulmányainkban azonban megerősítést nyert, hogy a javasolt algoritmus SNR-je adja a legjobb eredményt. Ráadásul a konvergencia sebessége gyorsabb, és a számítások összetettsége kisebb, mint az LMS implementációk esetében. Az eredményeket az 1. táblázatban mutatjuk be.
SNR szűrés előtt (dbs-ben)