A játékelmélet alapfogalmai
A játékelmélet célja a konfliktushelyzetek megoldása. azaz Olyan helyzetek, amelyekben két vagy több fél különböző célokat követelő érdekei ütköznek egymással.
Ha a felek célja közvetlenül ellentétes, akkor egy ellentétes konfliktusról beszélnek.
A játék egy konfliktushelyzet egyszerűsített formalizált modellje.
A játék egyszeri rajzát elejétől a végéig pártnak nevezik. A tétel eredménye fizetés (vagy győzelem).
A játék mozog. azaz választani a játékosok számos lehetséges alternatíva.
A mozdulatok lehetnek személyesek, véletlenszerűek. szemben a véletlenszerűen. egy változat játékosának tudatos választása feltételezi.
Olyan játékokat, amelyekben legalább egy személyes lépés van, stratégiainak nevezik.
Azok a játékok, amelyekben minden mozdulat véletlenszerű, nevezik szerencsejátéknak.
A személyes lépés során a játékos stratégiájáról is beszélnek, pl. A játékszabály kiválasztására vonatkozó szabály vagy szabálykészlet. Ebben az esetben a stratégiának átfogónak kell lennie, azaz. A választást a játék során esetlegesen felmerülő esetleges helyzetekben kell meghatározni.
A játékelmélet feladata megtalálni a játékosok számára optimális stratégiákat, azaz olyan stratégiákat, amelyek maximális nyereményt vagy minimális veszteséget biztosítanak számukra.
A játékelméleti modellek osztályozása
A n játékosok játékát általában úgy nevezik, mint ahol
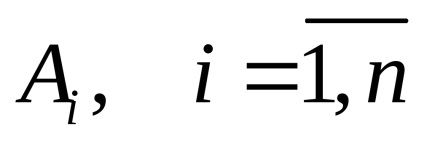
Ennek a kijelölésnek megfelelően javasolt a játékelméleti modellek alábbi osztályozása:
Diszkrét (stratégiák készlete

Folyamatos (stratégiák készletei)

Antagonisztikus (nulla összegű játék)
(a felek érdekei ellentétesek, azaz egy játékos elvesztése megegyezik a másik nyereményével)
Teljes információval (ha a játékos személyes mozdulatot készítő játékos tudja a játék teljes őstörténetét, vagyis az ellenfél összes mozdulatát)
Hiányos információkkal
Zéró összeggel (a teljes kifizetés nulla)
Nem nulla összeggel
Pár antagonista játék mátrix ábrázolása
Ebben a kézikönyben két ember ellentétes játékát tekintjük. a mátrix formában megadva. Ez azt jelenti, hogy ismerjük az első játékos (A játékos) Ai>, i = 1, ..., m stratégiáit és a második játékos stratégiáit (B játékos) Bj>, j = 1.n. és az A = || aij || mátrix is az első játékos nyer. Mivel ez egy ellentétes játék, feltételezzük, hogy az első játékos nyereménye megegyezik a második játékos elvesztésével. Feltételezzük, hogy a mátrix aj eleme az első játékos nyeresége, amikor az Ai stratégiáját választja, és válaszol a második játékosra a Bj stratégiával. Az ilyen játékot a következőképpen jelölik meg
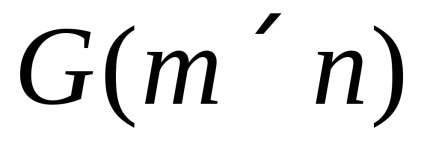
Nem nehéz látni, hogy ez a játék ellentétes, ráadásul ez nem teljes információval rendelkező játék B játékos személyes mozdulattal nem tudja, milyen választási lehetőséget adott a játékos.
Mint már említettük, a játékelmélet problémája az, hogy megtaláljuk a játékosok számára az optimális stratégiákat, azaz olyan stratégiákat, amelyek maximális nyereményt vagy minimális veszteséget biztosítanak számukra. Ez a folyamat a játék döntése.
Amikor a játékot mátrix formában választja, ellenőrizze a játékot egy nyeregpont jelenlétének ellenőrzésére. Ehhez két értéket kell megadni:
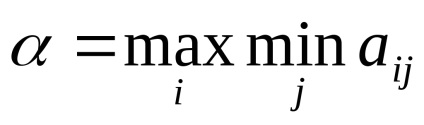
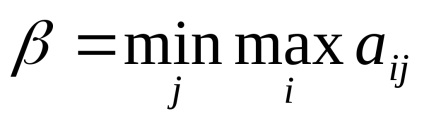
Az első játékos legvalószínűbb választja azt a stratégiát, amelyben a második győztes minden lehetséges válaszánál a legnagyobb győzelmet kapja, a másik pedig a saját veszteségét minimálisra csökkenti. lehetséges győzelem az első.
Bizonyítható, hogy α ≤V≤ β. ahol V a játék ára. azaz az első játékos várható nyereménye.
Ha az α = β = V reláció teljesül. akkor azt mondják, hogy a játéknak nyeregpontja van
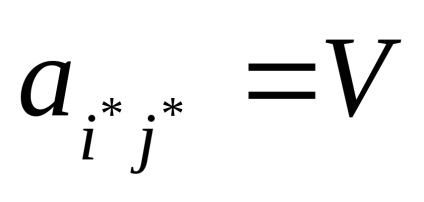
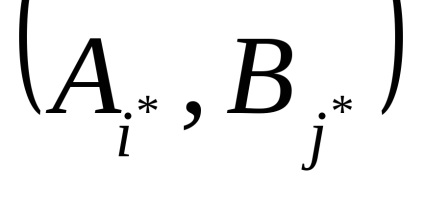
Térjünk vissza a játékba, amelyet az 1. példában megvizsgálunk, és ellenőrizzük egy nyeregpont jelenlétét.
Ez a játék teljes információval rendelkezik.
Ebben az esetben
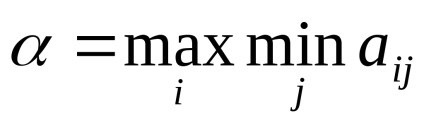
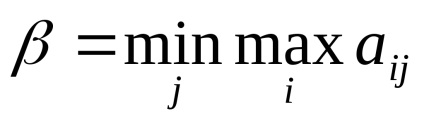
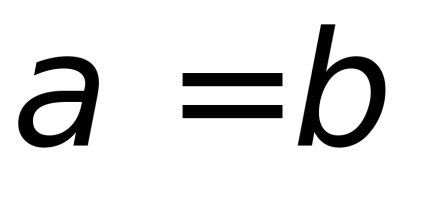
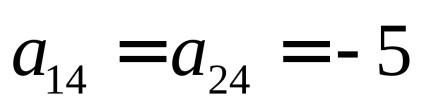
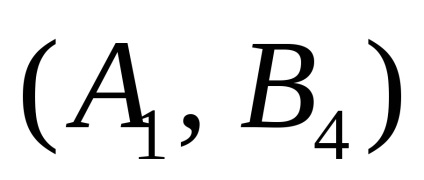
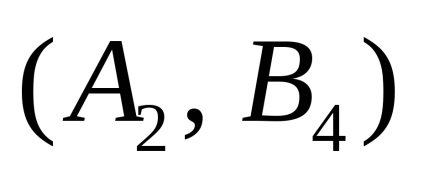
A 2. és a 3. példa a következő tétel tükrözi a játékelméletben:
Minden párt antagonisztikus játék, teljes információval megoldható a tiszta stratégiák.
így Az 1. tétel szerint minden két, teljes információval rendelkező játéknak nyeregpontja van, és két tiszta stratégia létezik
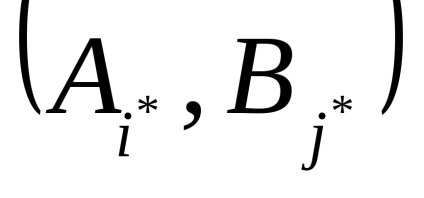
Vsluchae azonos hiánya nyeregpontja, használt oldatok t.n.smeshannye stratégia gdepiiqj - kiválasztási valószínűségeket Bj strategiyAi, és az első és a második játékos, ill. A játék megoldása ebben az esetben egy pár vegyes stratégia
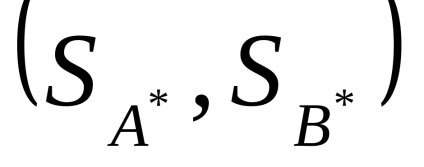
A következő tétel az 1. Tétel általánosított értelmezését jelenti egy hiányos információval rendelkező játék esetében:
Bármilyen páros antagonista játéknak legalább egy optimális oldata van, azaz páros a vegyes stratégiák általános esetében
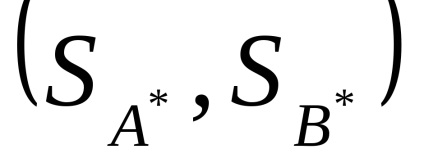
A konkrét esetben egy nyeregpontú játék esetében a vegyes stratégiák megoldása úgy néz ki, mint egy pár vektor, amelyben egy elem egyenlő egy, a fennmaradó pedig nulla.