A floyd-warshell algoritmus végrehajtása c
A szokásos Floyd-Warshell algoritmus végrehajtásához szükségem van arra, hogy az MPI könyvtár segítségével párhuzamosan kiszámítsam ezt a feladatot. Hamarosan beszámolok a párhuzamosság eredményéről (nagyon remélem). És most beszéljünk a Floyd-Warshell szabványos algoritmusáról.
A Floyd-Worshell algoritmus lényege
Mint említettem, az algoritmus célja, hogy megtalálja a legrövidebb útvonalat a gráf összes csúcsa között. Tény, hogy egyszerűen keresi az összes útvonalat, és a választásuk a legkevésbé. A keresést az NxN méretű úgynevezett "szomszédsági mátrix" végzi, ahol N a gráf csúcsainak száma.
Az i-es sor metszéspontjában és a mátrix j-os oszlopában az i csúcstól a j-csúcsig terjedő él súlyának értéke. A szomszédsági mátrix fő átlója mindig nulla, mert az i-th gráfban az i-edik csúcsból nincsenek szélek. Abban az esetben, ha a csúcsok között nincsenek szélek, a feltételes végtelenség (INF) a mátrixban lesz.
A Floyd-Worshell algoritmus megvalósítása
A legkisebb távolság keresése az összes útvonal egymást követő keresésével történik. Három ciklusban a külső választja a csúcsot, amelyen keresztül megpróbáljuk megtalálni a legjobb módszert. A belső két rendezi a csúcspontokat, amelyek között keressük a minimális távolságot.
A szomszédsági mátrix leginkább a következő formában tárolódik: az első sor a csúcsok száma, majd maga a mátrix. Végtelen hosszú távolságként (INF, ha a csúcsok nem kapcsolódnak egy élhez) egy meghatározott konstansot vesz fel. A megvalósításomban ez 101, ami azt jelenti, hogy a szél maximális súlya nem lehet 100-nál több.
Példa egy mátrixfájlra
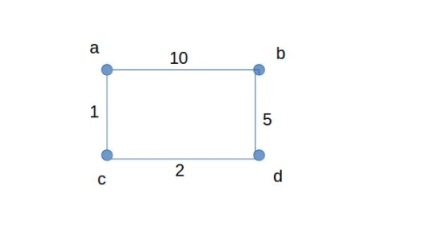
Az algoritmus forráskódja
Példa egy algoritmussal való együttműködésre
következtetés
A szokásos Floyd-Warshell algoritmus nagyon egyszerűen működik, de nagyon jól működik nagy mátrixokon. Ideális jelölt az MPI könyvtárnak való átadásához. A mai napig mindennek köszönhetően köszönöm figyelmedet.