Számjegyekkel ellátott vetületek
1.3. Felszíni számítással ellátott előrejelzések
A numerikus jelekkel ellátott vetületek felületét általában a kontúrok határozzák meg. A felszíni horizontok ezen felületek metszetvonalaként ábrázolhatók vízszintes síkokkal, amelyek állandó pályán vannak rajzolva. Az ilyen kontúrok kialakítása a felszín osztályozásának feladata. A felületekre alkalmazott meredekségi vonal általában egy adott pontra vonatkozik, és merőlegesen húzódik az áthaladó vízszintes vonalakra.
A besorolási probléma egy gyakran tapasztalt probléma, amelyet a numerikus jelekkel rendelkező vetületek felületével kapcsolatban megoldottak.
Nézzük meg a probléma megoldását bizonyos felületekre.
a. Kúpos felület
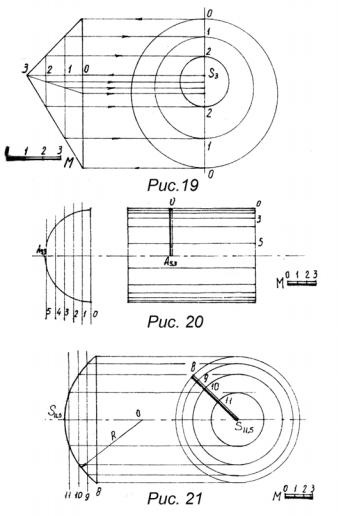
A kúpfelület függőleges tengelyű egyenes kúpként és ferde kúpként ábrázolható, először egy egyenes kúpot (18. Ábra, a). A kúpos felület szelvényei vízszintes síkokkal egy sor kört adnak. Egyenes kúp esetében vízszintes síkra vetítve egy sor koncentrikus kört kapunk (18. ábra, b). A közvetlen kúp legnagyobb meredekségének vonala a kúp generátorának osztályozásával érhető el. A művelet elvégzéséhez ismerni kell a generátor bármely két pontjának jelét, vagy egy pont és a lejtő jelét.
A helyzet kissé bonyolultabb, ha a kúp hajlik. A párhuzamos síkokban levágott körök középpontjai nem fekszenek egy függőleges tengelyen, ezért ha vízszintes síkra
koncentrikus körök formájában nyújtson előrejelzéseket. A kalibrációs ferde kúp (ábra. 19) van kalibrálva, hogy a leghosszabb és a legrövidebb generátort. Pontosítsa a generátorok azonos jelölőpontjait, jelöli, hogy a kör átmérője vízszintes. Ahhoz, hogy megtalálja a közepén ez a kör használhatja a választóvonal intervallum (átmérő) két egyenlő részre, vagy mint a 19. ábrán látható, a függőleges tengelyen, hogy tartsa a vetítési kúp, amely ezek a központok a körök tartoznak.
b. Hengeres felület
Ha a henger generátorai függőlegesek, akkor a henger vízszintes vetülete kör, azaz degenerált. Ebben az esetben a numerikus jelzésekkel ellátott vetületekben a henger tetején lévő jelölés látható a degenerált vetületen. Ebben az ügyben nincs különösebb érdeklődés. Ha a henger tengelye vízszintes, akkor a felület osztályozásának problémája csökken azon generátorok feltárásához, amelyeknek jelölései egész számok. Ehhez a henger függőleges vetülete vagy annak egy része kiépítésre kerül, amelyet meg kell mérni (20. ábra). Magasságban osztályozva, vízszintes síkok függőleges vetületeit hajtjuk végre. Megemlítjük a henger függőleges vetületeinek metszéspontjait, és az ismeretlen generátorok vetületeinek numerikus jelölésével továbbítják a vetületbe. A lejtővonal egy ilyen felület bármely pontjára egy körív.
a. Gömbölyű felület
A gömbfelület átvágása ugyanolyan elvvel történik, mint egy hengeres felület kalibrálása (21. ábra). A gömb függőleges vetülete felépítésre kerül, függőleges tengelyét osztályozzák, a vízszintes síkok függőleges vetületének metszéspontjai és a gömb függőleges vetülete található. Ezután a gömb elülső vetületén a körök sugarait jelölik, amelyek levágják a gömb felületén lévő vízszintes síkokat. Ezek a sugarak tartják a kívánt köröket, amelyek a gömb horizontálisak a vetületen numerikus jelekkel. A gömbfelület bármely pontjának lejtős vonala egy körív.
Az egyenlõ meredekség városa
Ha a csúcsonként egyenes kör alakú kúp egy tetszőleges görbe mentén mozog (22. ábra), az ezzel az elmozdulással kapott felületet egyenlő lejtésű felületnek nevezzük. A kúp a felület meghatározója, és a görbe útmutatóként szolgál. Az ilyen felület bármely pontján a lejtővonal ugyanolyan meredeksége van a vízszintes síknak. Az ugyanazon rámpa felületének kalibrálása során figyelembe kell venni, hogy a felszín meredeksége bármely pontján ugyanaz, és a szomszédos vízszintek közötti távolság megegyezik a lejtős vonal intervallumával. Az osztályozáshoz helyezzük a kúpokat az adott görbék pontjára, és méretezzük a felületüket. A gyakorlatban (23. ábra) ez úgy tűnik, hogy a görbe pontjai elé állítják a koncentrikus köröket, amelyek sugarai különböznek az intervallum értékétől és a magasságjelek egyenként. A kúpos felületek horizontális felületét érintő ívelt vonalak rajzolásával, amelyek azonos jelzéssel rendelkeznek, az egyenlő lejtő felszínének látószögét kapjuk.
1. Mi a szokásos definíciója a felületek numerikus jelölésekkel rendelkező vetületeinek?
2. Melyek a felszíni kontúrok?
3. Mit jelent felvenni?
4. Melyek a kúp horizontái?
5. Mi a különbség az egyenes és a ferde kúp beosztása között?
6. Mi köze van a gömb alakú és hengeres felületeknek?
7. Melyek a hengeres felület horizontái?
8. Mik a gömb alakú felület horizontái?
9. Mi az egyenlő előítélet felülete?
10. Mi az egyenlő lejtésű felület meghatározója?
11. Mi az egyenlő lejtő felületi vezetője?
12. Hogyan osztályozható az egyenlő gradiens felülete?
1. Húzza át a hengeres felületet (24. ábra).
2. Húzza fel egyenlő lejtésű felületet (25. ábra).
1.3. Topográfiai felület
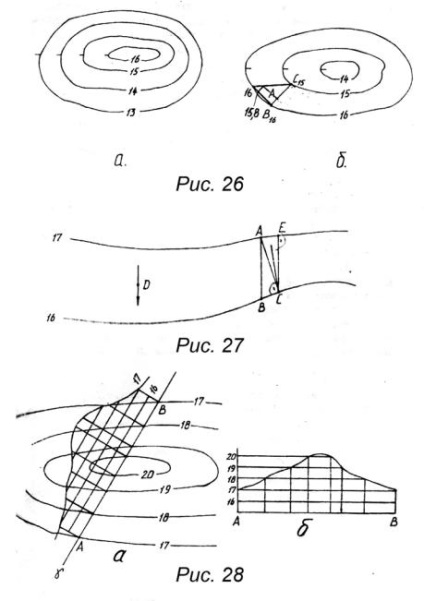
A földfelszíni (topográfiai) felületet a keretmodell vízszintes vetülete jelenti, amelyet a Föld felszíne vízszintes síkokkal történő boncolása okoz. Ahogy a kontúrok nőnek, meg lehet ítélni a megjelenített felület típusát. Tehát a 26. ábrán látható a a terep (hegy) növekedése és a 26. ábra b csökkenése. A vízszintes magasságokon kívül a Bergstriks általában a terep esése irányát mutatja. Fontos feltételezés a numerikus jelek előrejelzéseiben a lineáris karakter feltételezése a terep változásának lineáris jellege között. Ez a feltételezés lehetővé teszi számunkra, hogy megoldjuk a következő problémákat:
1. Keresse meg a terep közbenső pontjainak jelöléseit (26. ábra, b).
Például az A pont jelzésének meghatározásához tetszőleges irányú szegmenset rajzolunk át rajta. A szegmens kezdete (azaz B) és vége (azaz C) az A ponthoz kapcsolódó szomszédos pontokon helyezkedik el. A szegmens beosztásának megfelelő művelet végrehajtásával (lásd 1.1. §) meghatározzuk az A pont (-15.8.) Jelét.
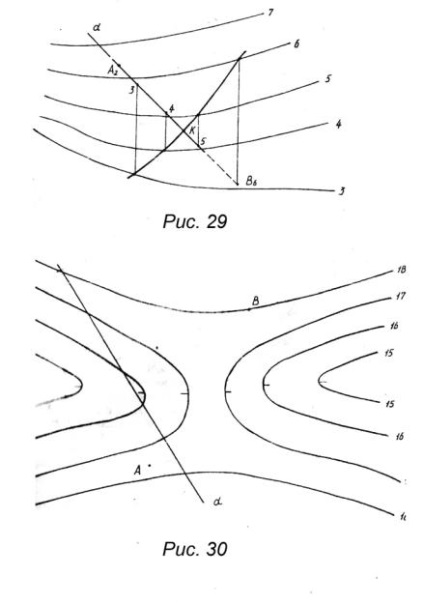
2. Készítse el a felszín lejtését (27.
Például, az irányt a vonal a legnagyobb emelkedő D pontban egybeesik az irányt a merőleges levonni ezen a ponton, hogy a szomszédos vízszintes irányába csökken jelek (nyíl jelzi). Meghatározása lejtése a vonal önmagában, egy tetszőleges pontja a felület (. A mi esetünkben R A) a következő:
A szomszédos vízszintesre merőleges (C. C). Mivel a görbült felület, a merőleges felépült t. C, az ellenkező irányba, a kiindulási pont nem egyezik, és lenne azon a ponton, E. ACE szögfelező lesz irányba vonal legnagyobb lejtését a legközelebbi a referenciapont egy felületi pont. Az A pontnál a legnagyobb rámpa vonala párhuzamos az ACE szögfelezőjével.
3. Határozza meg a topográfiai felület szakaszvonalát a kiálló síkkal. Ilyen szakasz (28. ábra, a, b) a felületi profilnak nevezzük. A secant síkot a vízszintes vetület γ adja. Figyelembe véve a sík metszéspontjait a felület kontúrjaival, felépítünk egy felületi profilt. Ehhez egy olyan alapot választunk, amely vízszintes, vagy kissé alacsonyabb, a terep horizontjának minimális jelével, amelyet a γ sík keresztez. Merőlegesen követte a vonal síkját
felvetettük a megfelelő kontúrok jelét, és egy sima görbével összekötöttük őket. Tipikusan a vízszintes skála nagyobb, mint a vízszintes skála, amelyben a kommunikációs vonalak mentén a függőleges magasságok lerakódnak. Ebben az esetben a kapott profil sokkal kifejezőbb. A profilra vízszintes rácsot alkalmaznak. Az első profilhorizontot alapprofilnak nevezik. A profil egymásra helyezhető, amint azt a 28. ábrán, a ábrán vagy ábrázoltuk (28. ábra, b). Rendezett profil esetében a rajzon tetszőleges helyen található, tetszőleges tájolással a vágási sík nyomvonalához képest (lásd a grafikai feladat végrehajtásának mintáját).
4. Keresse meg egy egyenes vonal metszéspontját egy topográfiai felületen (29. ábra). Ez a feladat a következő szakaszokra oszlik:
a. Végrehajt egy adott AB vonalat;
b. Megállapítjuk az egyenes vonalat az α általános pozíció síkjában; a. Keresse meg az adott sík körvonalainak metszéspontjait a kontúrokkal
topográfiai felülete (mint a síkban, amely abban rejlik közvetlenül van egy tetszőleges orientációban, a vízszintes sík az, fennmaradó egymással párhuzamosan, az AB vonal a megdöntött egy tetszőleges szögben);
d) Miután összekapcsoltuk a sima görbével kapott pontokat, megkapjuk az a sík és a topográfiai felület metszésvonalát. E vonal és az adott vonal metszéspontjában a topográfiai felület és az AB vonal metszéspontja a kívánt K pont.
1. Mi nevezik topográfiai felületnek?
2. Melyek a Bergstriks céljai?
3. Mi a feltételezés a kontúrok közötti terepi változások természetéről?
4. Melyik vízszintes vonalat kell alapnak nevezni a terepprofil ábrázolásakor?
5. Mi a különbség a felhalmozott terepprofil felépítése között?
1. Határozza meg a topográfiai felület A középtengelyének jelölését (30. ábra).
2. Építsd fel a legnagyobb felszíni lejtés vonalát a B ponttól kezdve (30. ábra).
3. Hozzon létre terepprofilt az α szekvenciasíma adott pályamenti irányában
2 AZ EPIUR TELJESÍTÉSÉRE VONATKOZÓ UTASÍTÁSOK
A rajz kereteit és a főbb feliratok keretét kirajzolva meg kell rajzolni az építési terület területének topográfiai tervét. Akkor vegye fel a földmunkák tervét. A rajz méretét három vagy négy alkalommal kell növelni a feladat skálájához képest. A feladat változata az alkalmazásban van. A változó számát a tanár állítja be. Az építési tervben a következő feladatokra van szükség:
1. A földmunkák ásatásainak lejtői és a földes építmények lejtői metszésvonalainak megépítése.
2. Területi felépítésű ásatások és töltések lejtői metszésvonalainak felépítése.
3. A földrajzi és földmunkák profilját az A-A irányába kell felépíteni.
Munkavégzés során az alábbi követelményeket kell figyelembe venni:
1. A rajzot A3 formátumú rajzpapír lapos ceruzával rajzolja.
2. A topográfiai felület látóterét a lejtők határáig folyamatosan vékony vonalakkal, valamint a lejtők - szaggatott vonalak között végzett ásatások határai között húzzák. A vonalak vastagsága 0,1 ... 0,2 mm.
3. A földmunkák kontúrját és a lejtők metszésvonalát egy topográfiai felületen 0,5 ... 0,6 mm vonalvastagsággal húzzuk meg.
4. Bergstrihi az ásatások és a töltések lejtői merőleges a vízszintesekre,
egymással váltakozva
3. GYAKORLATI PÉLDA
3.1. A lejtés, a töltés és az útszakaszok meghatározása
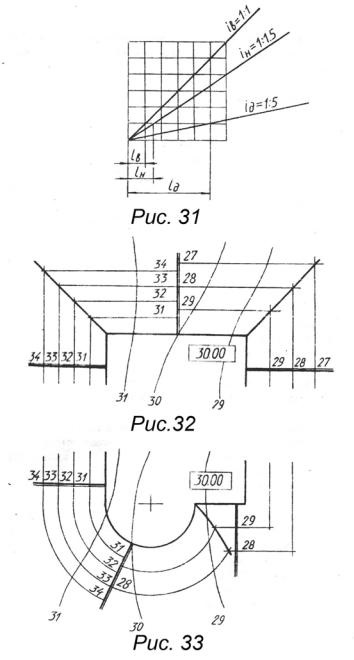
Az i = 1: 1 lejtők lejtőinek lejtését figyelembe véve az i = 1: 1.5, az i q = 1: 5 út meredekségének lejtése, a lejtők skálaát állítjuk össze (31. ábra).
Az egyik pontból levett függőleges és vízszintes egyenes vonal mentén felépítjük a lejtős vonalakat, meghatározva a szükséges számú cellát a függőleges és vízszintes vonalak mentén. Például az út lejtésének megépítésére egy négyzetet függőlegesen és ötre helyezzünk
vízszintesen. Ugyanakkor a lejtőn kapott skála alapján megnevezzük az ásatás (ℓ), a töltés (ℓ н) és az út (ℓ д) szakaszát.
3.2. A földszerkezet egyenes vonalú lejtői metszésvonalának megépítése
A földmunkák lejtői metszésvonalának megépítéséhez (32. Ábra) létrehozunk egy nulla vonalú vonalat, amely a terep 30. vízszintje mentén halad át. a földmunkák helyszíne 30-as jelzéssel rendelkezik. A terep harmincadik horizontális oldalától balra a feltárás a töltés jobb oldalán lesz. A terület határainál merőlegesen felépítjük az ásatás és a töltés lejtői meredekségét. A hely széleivel párhuzamosan a lejtő horizontalsit a 27, 28, 29, stb. Jelzésekkel végezzük a töltéshez, a 31, 32, 33, stb. A lejtők metszésvonalai egyenlő értékű kontúrok metszéspontján haladnak át.
3.3. Az egyenes vonalak és az ívelt lejtők metszésvonalának megépítése
A lejtők felszíne, amely a helyet egy félkörrel köti össze, része a kúpos felületnek, amelynek körvonala olyan koncentrikus félkörív, amelynek középpontja egybeesik a félkört középpontjával, amely a helyszínt határolja.
A lejtők metszésvonalának kialakítása (33. ábra) a következő sorrendben következik be:
1. A meredekség skála a helyszín egyenes vonalára merőleges. A topográfiai felület 30. vízszintes sarkától balra a mélyedés lejtős skálája, a töltés jobb oldalán.
2. Végezzük el a középen irányított íves lejtők és a domborzat lejtőinek nagyságát.
3. Végezzük el a derékszögű és ívelt lejtõk 27, 28 stb. Jelzõfalakat a töltéshez és a 31, 32 stb. Az egyenlő vonalú és kanyargós kontúrok kereszteződésein keresztül rajzoljuk a lejtők metszésvonalát.
3.4. A terület és az út lejtői metszésvonalának megépítése
A terület lejtője az út melletti úton (36. ábra) a parton található. A lejtők metszésvonalának meghatározásakor a 27, 28, 29 emelkedési pályák meredekség-emelkedési pályáit állították össze (32. és 33. ábra).
A lejtők körvonalainak megépítéséhez az utakat, amelyeknek tengelye egyenes vonalú, átmegyünk az úttestre. A 30-as ponttól az oldal szélétől az ℓ d intervallumokat az útmenti tengely mentén rajzzuk fel, és húzzuk az út horizontális részét.
Az út vízszintes vonalainak metszéspontjától az út szélén egy kör körvonalait vesszük fel, amely egyenlő az ℓ n intervallummal. amelyeknek a 28, 27, 26, stb. jelzései vannak. Az út horizontális metszéspontjaitól az élével érintő pontokat húzunk olyan körökhöz, amelyek pontokkal azonosak. A körök érintõi (34. ábra) az út lejtõjének horizontális lejtõi. A helyszín és az út lejtőinek egyértékű horizontális metszéspontjain át haladunk a lejtőkön.
Ha az útszakasz görbe, akkor a szerkezetek alapvetően nem különböznek a leírtak közül, de az út kontúrjai görbületi görbék, amelyek ugyanazokkal a jelölésekkel rendelkeznek.