Válaszok a geometria számára a 9. osztály - feladat, 2. oldal
12. A háromszög (formuláció és példa) szögeinek összegére vonatkozó tétel.
1. A háromszögben az egyik szög 29 °, a másik 91 °. Találd meg a harmadik sarokát.
A megoldás. A háromszög harmadik szöge
180 ° - (29 ° + 91 °) = 180 ° - 120 ° = 60 °.
2. Keresse meg az egyenesen álló háromszög éles szögeit.
A megoldás. A háromszög szögének összegéből származó tételből következik, hogy egy derékszögű háromszög akut szögeinek összege 180 ° - 90 ° = 90 °. Mivel egy éles, derékszögű háromszög éles szöge egyenlő, mindegyik egyenlő 90 ° -os. 2 = 45 °.
3. Keresse meg az egyenlő oldalú háromszög szögeit.
A megoldás. A háromszög szögeinek összegéből származó tételből következik, hogy az egyenlő oldalú háromszög szögeinek összege 180 °. Mivel minden szög egy egyenlő oldalú háromszögben egyenlő, mindegyikük 180 °. 3 = 60 °.
13. A háromszög megoldása három oldalról.
Oldja meg a háromszög három oldalát - ez azt jelenti, hogy a szögeket a háromszög három oldalán találja meg.

A probléma megoldásának egyedisége a háromszög egyenlőségéből következik:
Ha az egyik háromszög három oldala egy másik háromszög három oldalával egyenlő, akkor az ilyen háromszögek egyenlőek.
14. A "A trapéz középvonalának" témája.

15. A jobb szögű háromszög akut szögének szinuszának meghatározása. Példa a négyszögletes háromszögek megoldására.
A jobb háromszög akut szögének szinája az ellentétes láb és a hypotenuse aránya:
1. Jobb háromszög. Keressétek meg: a) a c hipoténszeciát és az L katétet, ha egy cathetuszt és egy ellentétes szöget adunk hozzá;
b) az a és b háromszög lábai, ha a c hipoténszekvencia és az a akut szög egyikének van megadva (12. ábra).
2. A hegy tetején egy 1,2 km hosszú, egy 60 ° -os szöget zár be a hegy magasságával. Mi a hegy magassága?
A megoldás. Jelölje meg a kötél hossza c-on keresztül, a hegy magassága az A-n keresztül, valamint a felvonó és a hegy magassága közötti szög (3 (13. ábra).
Tekintettel: c = 1,2 km, p = 60 °.
A megoldás. Egy háromszög szögének összegéből származó tételből következik, hogy egy derékszögű háromszög akut szögeinek összege 90 °. Ezért a = 30 °. Innen
16. Egy egyenlő háromszög szögének tulajdonsága.
Úgy mondják, hogy egy háromszög izoszceles, ha két oldala egyenlő. Ezeket az egyenlő oldalakat oldalaknak nevezik, a harmadik pedig a háromszög alapja.
[P] Egy egyenlő háromszögben az alapfelületek szöge egyenlő.
Tekintettel: ABC - egyszárnyú háromszög, AB-alap (14. ábra).
Bizonyítsd: szög A = B szög.
Bizonyítás. A CAB háromszög egyenlő az egyenlőség első jeleivel a CBA háromszögnek

17. A "Háromszög hasonlósága" problémája.

18. Feladat a "Parallelogram" témában.
A egyenlőszárú háromszög felirat olvasható paralelogramma úgy, hogy a szög a paralelogramma egybeesik csúcsszöge a háromszög, és a csúcsszög az ellenkező földön fekvő. Bizonyítsuk be, hogy a paralelogramma kerülete egy adott háromszög állandó értéke.

19. A jobb háromszög akut szögének koszinuszának meghatározása. Példa a négyszögletes háromszögek megoldására.
A jobb háromszög akut szögének koszinusa a szomszédos láb és a hypotenuse aránya:
1. Jobb háromszög. Keresés:
a) a c hipoténsze és a katéter a, ha a b kathetet és a szomszédos szöget megadják;
b) az a és b háromszög lábai, ha c hipoténuszot és az egyik acut szög egyikét adjuk (a 16. ábra).

2. A mozgólépcső és a csarnok szintje közötti szög 150 °. Mekkora a mozgólépcső létrájának hossza, ha a lépcső alja 117 m?

20. Egy egypólusú háromszög jele.
Úgy mondják, hogy egy háromszög izoszceles, ha két oldala egyenlő. Ezeket az egyenlő oldalakat oldalaknak nevezik, a harmadik pedig a háromszög alapja.
[P] Ha két szög egy háromszögben egyenlő, akkor egyenlő.

Bizonyítás. Mivel a háromszögben a két szög egyenlő, az oldalak ezen szögek mentén egyenlők. Sőt, ha feltételezzük, hogy e felek több, mint a másik, akkor a szög vele szemben, nagyobb, mint a szög, feküdjön fel a másik fél, és ez ellentmond a hipotézist (a tény, hogy ezek a szögek egyenlő). Tehát a háromszögben a két oldal egyenlő, vagyis a háromszög egyenlő.
21. A "Háromszög hasonlósága" problémája.
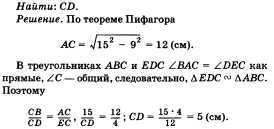
22. A téma "Téglalap" témája.
A téglalap oldalai 5 cm és 4 cm-esek. A nagyobb oldali szomszédos sarkok szélei három részre osztják az ellenkező oldalt. Keresse meg ezeknek a részeknek a hosszát.

23. A jobb háromszög akut szögének érintője meghatározása. Példa a négyszögletes háromszögek megoldására.
A jobb háromszög akut szögének érintője az ellenkező aránya
egy láb a szomszédos:
1. Jobb háromszög. Keresés:
a) a c hipoténszekvencia és az L katéter, ha egy cathetuszt és egy ellentétes szöget adunk hozzá;
b) a c hipoténszekvencia és az a katéter, ha b katétert és egy szomszédos a szöget kapunk (a 20. ábra).

2. milyen szögben esik a földre sugár a nap, ha a függőleges rúd a földbe emelkedik a talajszint felett 18 m és árnyékot vet egyenlő 73 6 (ábra. 21)?
Jelölje meg a pólus hosszát a, a pólus árnyékának hosszát a b segítségével, valamint azt a szöget, amelyen a nap sugara a földön történik, a.
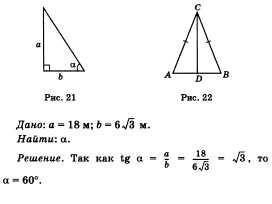
24. Az egysíkú háromszög medianjának tulajdonsága.
Egy oszlopos háromszögben az alapra húzódó medián egy bisectrix és egy magasság.
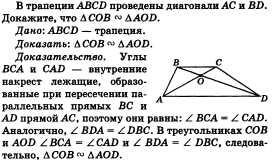
Tekintettel: ABC - egyszárnyú háromszög, AB - alap, CD - median (22. ábra).
Bizonyítsd: CD - felező és magasság.
Bizonyítás. Háromszögek CAD és a CBD egyenlő, de a második jellemző az egyenlőség háromszögek (oldalán AC és BC egyenlő, mint az ABC - .. Isosceles szögek CAD és CBD szögei alján egy egyenlő szárú háromszög oldalai AD és BD egyenlő, mivel a D - középső szegmenst AB).
A CBD és a CAD háromszögek egyenlősége magában foglalja a szögek egyenlőségét:
Mivel az ACD és a BCD szöge egyenlő, a CD egy felező. Mivel az ADC és a BDC szögek egymással szomszédosak és egyenlők, egyenesen vannak. Következésképpen a szegmens CD az ABC háromszög magassága is. A tétel bizonyított.
Így megállapítható, hogy a bázissal, a középsõvel és az egyenlõs háromszög magasságával, az alapra húzva, egybeesik. Ezért a következő állítások is igaz:
1. Az alapra húzódó egyszárnyú háromszög felezője medián és bisectrix.
2. Az alapra húzódó egyszárnyú háromszög magassága medián és bisectrix.
25. A "Háromszög hasonlósága" problémája.
26. A "Diamond" téma feladata. Négyzet ".
Bizonyítsuk be, hogy egy kört beírhat egy rombuszba.
Adott: ABCD - rombusz, O - a rombusz gyémántja metszéspontja.
Bizonyítsd be: O az írott kör középpontja.
Bizonyítás. Háromszögek ABO, ADO, CBO és CDO - téglalap (mivel ABCD - rombusz), és végig a átfogója és egy láb. Következésképpen az egyenes szögek csúcsaiból levont OF és OE magasságok egyenlők. Tehát az alap magasságban fekszik egy kör közepén O. mivel a magassága levonni csúcsain derékszögben, merőleges oldalán a rombusz, az O középpontú kör - a metszéspontja az átlók rombusz - és amelynek sugara megegyezik a távolságot O pont az oldalán, a rombusz, a felek között rombusz. Ennek következtében egy kört írhatunk a rombuszba.
27. A koszinus tétel. Példa a háromszögek megoldására.
A háromszög egyik oldalán lévő négyzet egyenlő a másik két oldal lábainak négyzetének összegével anélkül, hogy megduplázná az oldalak termékeit a köztük lévő szög koszinusával.

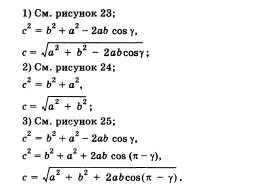

28. Egy háromszögbe írt kör.
Azt mondják, hogy egy kört háromszögbe írnak, ha minden oldalát megérinti.
[Π] Tétel a háromszögbe írt kör közepén.
A háromszögbe írt kör középpontja a bisectrix metszéspontja.
Tekintettel: az ABC egy adott háromszög; O a kör középpontja; D, E és F a kör érintkezési pontjai a háromszög oldalával (27. ábra).
Bizonyítsd be, hogy O a szelvények metszéspontja.
Bizonyítás. A négyszögletes háromszögek AOD és DOE egyenlőek a hypotenuse és a láb. Egy OA-val rendelkező hipotenuzus van, és az OD és OE lábak egyenlőek a sugárral. A háromszögek egyenlősége az OAD és OAE szögek egyenlőségét jelenti. Ez azt jelenti, hogy az O pont az A csúcsból levezetett háromszög felezőpontján fekszik. Pontosan ugyanúgy bebizonyosodik, hogy az O pont a háromszög két szelvényén fekszik.
[A] Tétel a háromszögbe írt körön.
A kör bármelyik háromszögbe felvehető.
Adott: A ABC - a háromszög, On - a metszéspont a szögfelező, M, L és R - a érintési pontján a kerülete a egy háromszög oldalainak (ábra. 28).
Bizonyítsd be, hogy: O az ABC közé helyezett kör középpontja.
Bizonyítás. Húzzon le függőleges OK, OL és OM-t az AB, BC és CA oldalakra az O pontból (lásd a 28. ábrát). Mivel az O pont egyenlő az ABC háromszög oldalán, akkor OK = OL = OM. Ezért, egy kör O középpontja sugarú OK átmegy a K pont L M. Az oldalán az ABC háromszög érintse a kört pontok K, L, M, mivel azok merőlegesek sugarak OK, OL és az OM. Ezért az OK sugarú kör középpontja az ABC háromszögbe van írva. A tétel bizonyított.
Megjegyzés. Ne feledje, hogy csak egy kör írható a háromszögbe. Valójában feltételezzük, hogy két kör alakítható ki egy háromszögben. Ezután a központ minden egyes kör egyenlő távolságra az oldalán a háromszög, és így egybeesik az O pont a metszéspontja a szögfelezői a háromszög, és a sugara egyenlő a távolság O pont a oldalán a háromszög. Következésképpen ezek a körök egybeesnek.
29. Feladat a "párhuzamos egyenes vonalak" -ra.

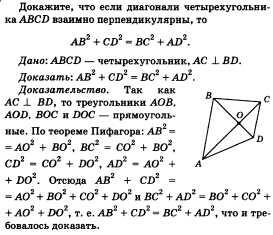
30. A "Pitagorasz-tétel" témája.
Bizonyítsuk be, hogy ha az ABCD négyszög átlói egymásra merõlegesek, akkor
Hasonló grafikák:
Általános megismétlés megszervezése a 7. fokozatú geometriai osztályokban
Tanfolyammunkák >> Pedagógia
Tanulmány a téma háromszögek a geometria tanfolyam 7-9 évfolyamos középiskolai
Tanfolyammunkák >> Pedagógia
. A „háromszögek” évfolyamon 7-9 1. igénypont összefoglalja órák témája „Jelek az egyenlő háromszögek” (tankönyvi Pogorelov AV Geometry munkájuk eredményét ösztönzik legjobb válaszokat Irányelvek: .. száma a rögzített bizonyítékokat.
Válaszok a vizsga kérdéseire a történelem Oroszország 11 osztályban. A könnyebb használat érdekében a kérdések és válaszok kronologikus sorrendben kerülnek közzétételre. NI Lobachevsky a nem euklideszi geometria forrásain állt. 1839-ben St. Petersburg Pulkovo V. Ya. Struve.
Válaszok a vizsgakérdésekre a történelem Oroszország 9 osztály. Források: kérdésekre / jegyekre adott válaszok. I. Lobachevsky a nem euklideszi geometria forrásain állt. 1839-ben Pulkovo alatt a. munkavállalók szakszervezetei, Komsomol for youth, úttörő szervezet a.
A filozófia kérdéseire adott válaszok a posztgraduális iskolákban
A természettudományos filozófia kérdéseire adott válaszok a posztgraduális képzésbe. a mechanikának feláldozik, és a geometriát a fő tudománynak nevezik. Fontos érdem. második terv. A német filozófiai osztályban ismét a természettudomány filozófiája szól.