A befektetési portfolió menedzsmentjének lényege és módszerei (10
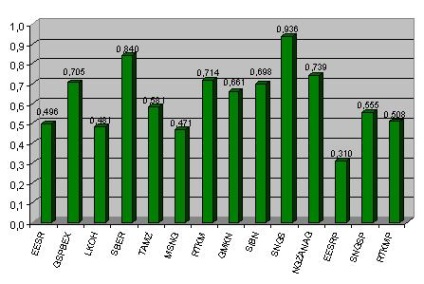
Ábra. 3.5 - Béta-egyenleg arány
Az optimális portfólió összeállításához elegendő a matematikai elvárásokat a múltbéli hozamok aritmetikai átlagaként meghatározni (3.6. Ábra). A matematikai várakozás nem tükrözi az állományi megtérülés tényleges előrejelzését, amely az összes befolyásoló tényező alapján történik, de elegendő matematikai modellek alkalmazása az optimális értékpapír-portfólió kialakításához.
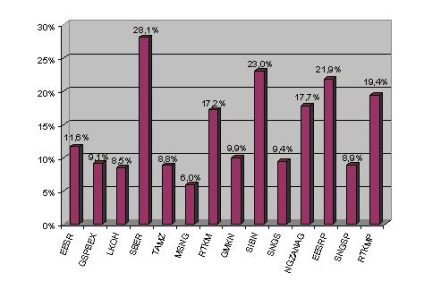
Ábra. 3.6. A részvény hozam matematikai várakozása
Most megtaláljuk az optimális portfólió struktúráját. A települések lebonyolításához kockázatmentes hozamot kell beállítania. A kockázatmentes kamatlábhoz a korábban kiszámított és évente 6% -kal megegyező hozamot az OFZ portfolión fogjuk elérni. Bár az államkötvények számított portfóliójában némi kockázat áll fenn, egyes feltevések szerint a hozam kockázatmentes lehet.
A portfólió várható hozama az értékpapírjainak megtérülésének matematikai várakozásainak súlyozott átlagaként kerül kiszámításra, ahol az ilyen értékpapírokba történő befektetések részesedése súlyként (17.
A 3.7. Ábra mutatja a számított állomány portfoliójának szerkezetét. A portfólió nem arányos részből áll: a fele a részvények tartsa 86,6% -a portfolió, a másik fele - csak 13,4%. A legnagyobb arányban osztják törzsrészvényeinek a Társaság „alapkezelő” olaj- és gázipari eszközök „(” olaj- és gázipari eszközök „) - 28,8% .A cég” Rostelecom „képviselteti magát a portfolió a kétféle részvények (rendes - 13,6%, előnyös - 15, 5%), akkor e portfólió legnagyobb része az adott vállalat részvényeinek (29,1%).
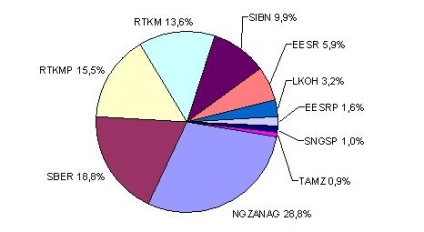
Ábra. 3.7. Az optimális részvényportfolió struktúrája
Az államkötvények és részvények optimális portfóliójának meghatározása nem elegendő az értékpapírok végső portfóliójának elkészítéséhez. Azt is el kell dönteni, hogy az alapok milyen arányban kerülnek befektetésre e portfóliókba.
Ezen arányok meghatározásához a Markowitz modellt alkalmazzuk, amelyet az optimális kötvényportfólió megtalálásakor alkalmazunk.
Ebben az esetben az a jellemző, hogy a megfontolt egységek nem egyedi értékpapírok, hanem maguk az értékpapír-portfóliók. Ezért a portfoliók hozamainak dinamikája érdekes lesz, és az egyes komponensek jövedelmezőségének dinamikáját nem veszik figyelembe.
A részvényportfolió készítésénél az a tény, hogy az árakat dollárban denominálták, nem befolyásolta a végeredményt a portfólióban lévő értékpapír részének formájában. Ebben az esetben a rubelben denominált kötvényportfolióval rendelkező kovariancia meghatározása esetén eltérések lehetnek. Ezért szükségessé válik a részvények nyereségességének újraszámítása rubelben a tőzsdei jegyzések alapján.
Az értékpapírok összesített portfóliójának optimális felépítésének problémájának megoldása érdekében a Markowitz modellt alkalmazzuk.
A lehetséges portfoliók hatékony csoportjának összeállításához szükséges a matematikai elvárás és a kovariancia mátrix kiszámítása.
A hónap kötvényportfólió hozamát úgy állapították meg, hogy egyszerűen elosztották az éves hozamot 12-tel. Az állomány portfóliójának heti hozamát havi sokszorosítással hány hétre csökkentették.
A portfolió hozam matematikai várakozása ebben az esetben nem számtani átlagként kerül kiszámításra, de az előző bekezdésben kapott várható jövedelmezőség elfogadott. Pontosabb érték.
A kovariancia mátrix összeállításához a portfolió-hozamok szórását és a korrelációs együtthatót kell kiszámítani (3.8. Táblázat).
A kovarianciákat a (18) képlet alapján számítják ki. Az eredményeket a 3.9 táblázat foglalja össze. A kötvények portfóliójának és a portfolió állományának kovarianziója megegyezik a négyszöges standard eltéréssel, vagyis ezeknek a portfolióknak a varianciájával.
Alapadatok az aggregált portfólió optimalizálására
Ezen adatok alapján hatékony portfólió-készletet lehet készíteni. A portfólió hozam matematikai várakozását a hozamok súlyozott átlagaként definiálják, ahol az adott biztonságban lévő befektetések aránya a súly (17. Az egyes portfoliók kockázatát a (18) képlet határozza meg. A számítások eredményeit a 2. függelék tartalmazza. Ezen adatok alapján lehetőség van egy lehetséges aggregált értékpapír portfólió hatékony összeállítására (3.8. Ábra).
Most meg kell határozni az optimális portfólió helyét, vagyis a jövedelmezőség és a kockázat elfogadható arányát.
Mivel a bankok nem nagy kockázatúak, a kívánt pontnak a görbe bal oldalán kell lennie - kevesebb kockázattal. Kezdve egy bizonyos ponton a görbe egyre finomabbá válik, jelezve, hogy a hozam további növekedésével a kockázat növekvő mértékben növekszik. Ezért célszerű olyan portfóliót elfogadni, amely 15,2% -os hozamot biztosít az adott befektető optimális portfóliójához.
Így ebben a portfolióban a kötvények 45% -át, a részvényeket 55% -kal képviselik.
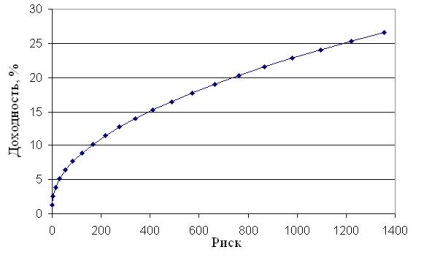
Ábra. 3.8. Hatékony aggregátum portfóliók
Eddig a portfólió összetételét relatív értelemben határozták meg. Az eredmények későbbi értékeléséhez abszolút értékek szükségesek. Ezért meg kell határozni a portfóliók mennyiségi összetételét. Ehhez ki kell választania a befektetett pénzeszközök összegét.
Abban az időszakban, amikor az Alfa-Bank aktívan részt vett az értékpapír-vételi és értékesítési ügyletekben, a befektetett pénzeszközök összege elérte az egyenleg pénznemének 15% -át. A mérleg pénzneme 340 millió rubel volt. Helyénvalónak tartom, hogy a beruházás összegére 5 millió rubelt, ami a valutaegyenleg mintegy 1,5% -a, és arányos a jelentési tételek értékével.
Így, figyelembe véve, hogy a források 45% -át fektetik az OFZ-be, és 55% -a részvények, úgy találjuk, hogy 2250 ezer rubel. irányítani kell az OFZ megvásárlására, a fennmaradó részre (2750 ezer rubel) - a részvények megvásárlására.
A vásárlási kötvények számát a következő képlet adja meg:
ahol Ki az értékes kötvények, egységek száma;
di - a kötvény által elfoglalt portfolió részaránya;
S - portfolióba fektetett alapok összege, rubel;
P% - a kötvény ára, névleges százalékában;
N - kötés megnevezése, dörzsölje.
A számításra és az eredményekre vonatkozó adatokat a 3.10. Táblázat foglalja össze.
Vásárolt kötvények számának kiszámítása
A részvények számának kiszámítása portfolióban történő vásárláshoz
A befektetés összege, RUR
3.3 Az Alfa-Bank értékpapír-portfóliókezelése modern körülmények között
Az OFZ portfóliójának változása kiszámítása