Véletlen események
A sigma-algebra elemét véletlen eseménynek nevezik.
Teljes rendezvénycsoport
Az események teljes csoportja a részhalmazok teljes csoportja, amelyek mindegyike esemény. Azt mondják, hogy egy teljes csoport eseményei az elemi eredmények helyének partíciói.
Legyen A legyen egy algebra. Funkció . az algebra leképezése a valós számok sorába
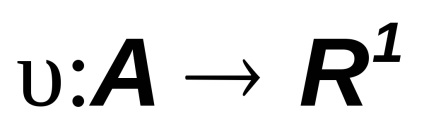
azt mondják, hogy finom additív, ha bármilyen véges párosan összeférhetetlen esemény
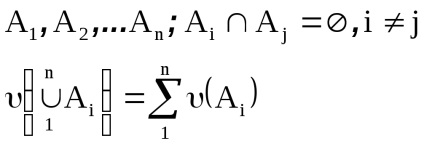
Legyen F egy algebra vagy egy sigma-algebra. függvény
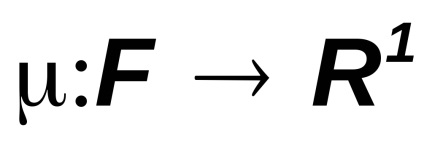
azt mondják, hogy megszámolhatóan additív, ha finom adalékanyag is van minden párosított inkompatibilis események
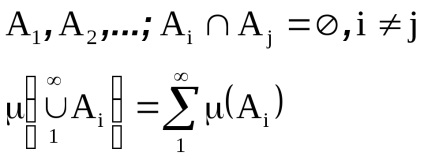
Egy intézkedés egy nem negatív, számíthatóan additív függvény, amelyet egy sigma-algebra kielégítő állapotban definiálnak
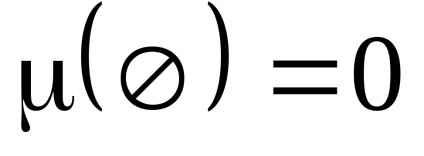
intézkedés

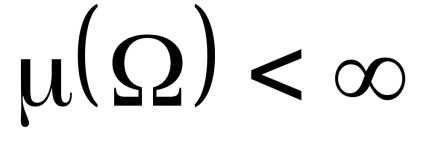
A P valószínűsége (valószínűségi mértéke) olyan mértékű. hogy
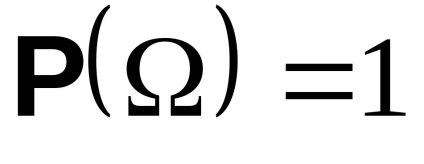
Mostantól leállítjuk a valószínűség százalékos megmérését, és kezdjük mérni valós számmal 0-ról 1-re.
Amikor P-t írsz, mindig képzeld el magadnak, hogy az elemi kimenetek és a sigma-algebra helyét értik. Ezután elkerülheti a sok hibát
Symbol P (valószínűség) valószínűségi egy szabványos, nem csak felejtsük el, hogy önmagában (anélkül, hogy meghatározná a tér elemi események és szigma-algebra) valószínűsége nem kerül meghatározásra.

az A esemény valószínűségének nevezzük
A valószínűségi hely
A valószínűségi hely három objektum gyűjteménye - az elemi kimenetek térsége, az események sigma-algebraja és valószínűsége.
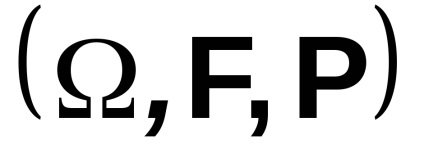
Ez egy véletlenszerű jelenség vagy objektum matematikai modellje.
A valószínűségi tér meghatározásának paradoxona
Térjünk vissza a valószínűségi elmélet problémájának kezdeti megfogalmazásához. Célunk egy véletlenszerű jelenség matematikai modelljének kialakítása volt, amely segítené a véletlen események valószínűségének számszerűsítését. Ugyanakkor a valószínűségi tér megteremtése érdekében meg kell határozni a valószínűséget, azaz úgy tűnik, pontosan az, amit keresünk (?).
Az állásfoglalás ez a paradoxon, hogy a teljes meghatározás valószínűség függvényében minden elemét F, általában elegendő meghatározni, hogy csak néhány esemény az F, a valószínűsége, amit könnyen azonosítani, majd kihasználva a megszámlálható additivitási számítva bármely elemét F.
Független események
A valószínűségelmélet fontos fogalma a függetlenség.
Az A és B események önállóak, ha
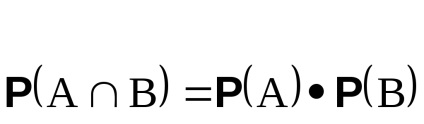
azaz Az események egyidejű megvalósításának valószínűsége megegyezik a valószínűségeik termékeivel.
A számlálható vagy véges sorozatban szereplő események páronként függetlenek, ha bármelyik pár egy pár független esemény
A számlálható vagy véges sorozatban lévő eseményeket függetlenül nevezik aggregátumnak. ha a véges részhalmazaik egyidejű megvalósításának valószínűsége megegyezik az ezen alcsoport eseményeinek valószínűségével.
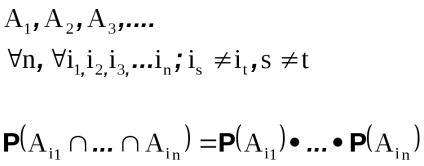
Nyilvánvaló, hogy a független események az aggregátumban függetlenek és párosak. Az ellenkező nem igaz.
Az A esemény feltételes valószínűsége, feltéve, hogy a B esemény bekövetkezett, a mennyiség
A feltételes valószínűséget jelenleg csak olyan B események esetében határozzák meg, amelyek valószínűsége nem nulla.
Ha az A és B események függetlenek, akkor
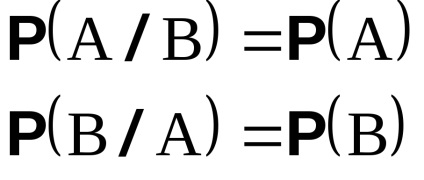
Tulajdonságok és tételek
A legegyszerűbb valószínűségi tulajdonságok
Az a tény, hogy az A és a nem-A ellentétes, és a valószínűség véges additivitásának tulajdonságaiból következik
Az ellenkező esemény valószínűsége
Az a tény, hogy a lehetetlen és a hiteles események ellentétesek
A lehetetlen esemény valószínűsége
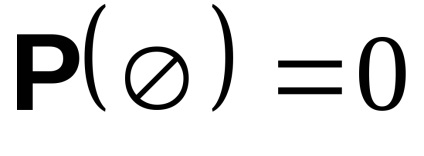
Ebből következik. hogy
és ebben az esetben
Ez abból a tényből következik, hogy minden esemény megtalálható az elemi eredmények térben