Laplace formulák
Az n nagy értékeinél a Bernoulli képlet együtt jár az időigényes számításokkal. Kiszámítsuk:
Ez nyilvánvalóan technikailag nehéz. Ilyen esetekben használja a képletet, ami a Bernoulli-képlet korlátozó esete.
A helyi Laplace-képlet. Ha az A esemény előfordulási valószínűsége p mindegyik tesztben állandó, és különbözik a 0-tól és 1-től, akkor annak valószínűsége, hogy az A-esemény k időben k n számú független próbában k elegendő nagyságú n értékkel közel azonos-e
ahol a Gauss-függvény (2.2.
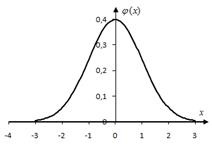
Minél több n. annál pontosabban (2.3). Ha kielégítő eredményeket ad a gyakorlatban.
A Gaussian függvény értékeit a B. függelék B.1. Táblázata tartalmazza.
A Gauss-függvény tulajdonságai:
1. egyenletes funkció; .
2. A függvény monotonikusan csökken az x pozitív értékei esetén. és (gyakorlatilag már feltételezhető, hogy már).
2.3. Példa. A prémium kategóriás termék gyártásának valószínűsége 0,4. Keresse meg azt a valószínűséget, hogy a véletlenszerűen kiválasztott 56 elem közül a felek a legmagasabb fokozatúak lesznek.
A megoldás. n nagy ,. ezért a helyi Laplace képletet (2.3) alkalmazzuk. Végezzük el a szükséges számításokat:
A következő Laplace-képlet lehetővé teszi annak megállapítását, hogy az A esemény n-ben független vizsgálatokban nem kevesebb, mint egynél kevesebb lesz.
Az integrált Laplace formula. Ha az A esemény minden valószínűségű eseményének valószínűsége p állandó, és különbözik a 0-tól és az 1-től, akkor annak valószínűsége, hogy az A esemény n-ben független vizsgálatokban legalább egyszer,
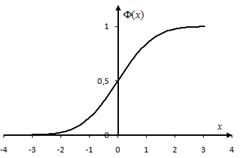
A Laplace funkció, (2.5)
Ha a (2.4) képlet általában szabálytalanságot ad a valószínűségszámítás hibájára, amely kielégítő a gyakorlatban.
A függvény értékei az alkalmazás B.2. Táblázatában találhatók. A grafikon a 2.3. Ábrán látható. A Laplace funkció tulajdonságait soroljuk fel.
1. A függvény páratlan, azaz.
2. A függvény monotonikusan növekszik, (gyakorlatilag feltételezhető, hogy már van).
2.4. Példa. Egyes területeken, minden 100 család közül 80-nak van hűtője. Mennyi a valószínűsége, hogy 300 és 360 család között, a megkérdezett 400-nál hűtőszekrény?
Jó példa lenne technikai
A megoldás. A Laplace képlet integrált formáját alkalmazzuk (először a képletekkel (2.6)
Továbbá a (2.4) képlet alkalmazásával, figyelembe véve a függvény tulajdonságait # 934; (x), kapunk:
(A B. melléklet B.2. Táblázatából :).
Tekintsük a Laplace integrált képlet következményeit.
Következmény. Ha az A esemény mindegyik vizsgálatban előforduló valószínűsége p állandó, és különbözik a 0-tól és 1-től, akkor elég nagy számú független kísérlet esetében a következő események valószínűségét a következő képletek határozzák meg:
a) az A esemény relatív gyakorisága az a és b között van:
b) az A esemény relatív gyakorisága az abszolút értéktől legfeljebb nagyságrendtől különbözik valószínűségétől:
Amikor és a Laplace formulák kielégítő hibát adnak a valószínűség gyakorlati kiszámításához. Ha n azonos rendű, 1 / n nagy n, vagy. A pontosabb eredmény a Poisson-képletet eredményezi
2.1. Hány részletezésre van szükség annak érdekében, hogy a legvalószínűbb felhasználható részek száma 50 legyen, ha a valószínűség, hogy a hibás rész 0,1.