Chi-négyzet eloszlás (téma)
Definíció. Adjuk meg a véletlen változókat ξ1. £ 2. ..., ξn függetlenek, és mindegyiknek normál normál eloszlása van N (0, 1). Azt mondják, hogy a χ 2n véletlen változó a következő:
,
egy chi-négyzet eloszlású szabadságfokokkal.
Ennek az eloszlásnak a jelölésére általában a χ 2n kifejezést is használják.
Nyilvánvaló, hogy χ 2n (minden η> 1 esetén) az 1. valószínűséggel pozitív értékeket vesz fel. Az χ 2n sűrűségfüggvény x (x> 0) pontban megegyezik
.
ahol r (-) - egy gamma funkció. A gyakorlatban ezt az eloszlási sűrűséget ritkán használják közvetlenül.
A khi-négyzet eloszlási sűrűségének különböző számú szabadsági fokú funkciói az alábbiakban láthatók.
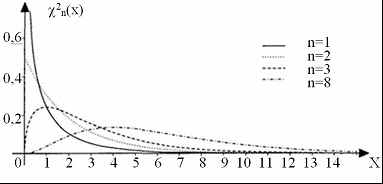
Ábra. Az eloszlásfüggvény egy chi-négyzet, amelynek különböző számú fokú szabadsága n
A χ 2n véletlen változó matematikai várakozása és varianciája megegyezik:
,
.
Egy χ 2n véletlen változó esetén különböző táblázatokat állítunk össze. Leggyakrabban a χ 2n véletlen változók p-kvantilenseinek értékeit tartalmazzák. n = 1, 2. m (ha a valószínűséget százalékban fejezzük ki, akkor százalékpontoknak nevezik őket, és ennek megfelelően száz százalékpontos táblázatokról beszélnek). Az p argument, 0<р<1, при этом пробегает тот или иной набор значений.