Alkalmazott problémák megoldása származék segítségével
Cél: az alkalmazott problémák megoldásának megtanulása származék segítségével.
Példa a feladatok elvégzésére
1. A test egyenes irányba halad egy adott törvénynek megfelelően.
a. Keressétek meg a test pillanatnyi sebességét az idő pillanatában.
b. Keresse meg a test felgyorsulását egy pillanatra.
c. Keresse meg, miután hány másodperc van az eredetétől, a test pillanatnyi sebessége = 44 m / s.
d. Keresse meg, miután hány másodperc az eredetétől a test gyorsulása egyenlő lesz.
a) A sebesség megtalálásához kiszámítjuk az elsőrendű származékot. Ezután a pillanatnyi sebességet 1 másodperc alatt.
b) A gyorsulás megtalálásához számítsa ki a második származékot. Ezután 2 másodpercen belül gyorsul.
c) Annak meghatározásához, hogy a test sebessége 44 m / s legyen, meg kell oldani az egyenletet. Kapunk t = 2 másodperc.
d) Annak meghatározásához, hogy a test gyorsulása 22 m / s 2 legyen, meg kell oldani az egyenletet. Még találni kell.
Vegye figyelembe, hogy ha a verzióban egy kötőjel van a megfelelő oszlopban, akkor ez az elem nem szükséges.
2. Húzza ki az érintő egyenletét a függvény grafikonjához
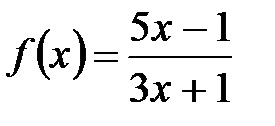
A probléma hipotézise x0 = 1 és f (x0) = f0 = 1. Az érintő egyenlete megegyezik
.
Így továbbra is megtalálható
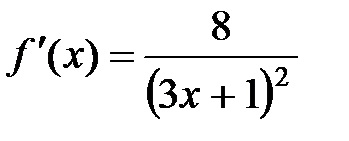
Ezután a tangens egyenlete megegyezik
1. A test egyenesen egy S (t) törvény alapján mozog.
a. Keresse meg egyszerre a test pillanatnyi sebességét.
b. Keresse meg egyszerre a test gyorsulását.
c. Keresse meg, miután hány másodperc van az eredetétől, a test pillanatnyi sebessége megegyezik.
d. Keresse meg, miután hány másodperc az eredetétől a test gyorsulása egyenlő lesz.
A test egyenesen az S (t)