Lineáris csoportkódok - számítástechnika, programozás
2. LINEAR CSOPORT KÓDOK
Egy lineáris egy olyan kód, amelyben a tesztszimbólumok az információ lineáris kombinációi. A csoportkód egy olyan kód, amely egy algebrai csoportot alkot a modulo 2 modul működéséhez képest.
Egy lineáris kód tulajdonsága: a lineáris kód kódvektorainak összege (különbsége) egy kódhoz tartozó vektort ad. A csoportkód tulajdonsága: a kódvektorok közötti minimális kód távolság a nem nulla vektorok legkisebb tömege. A kódvektor tömege megegyezik a kódkombináció számával.
A csoportkódok kényelmesen beállíthatók olyan mátrixokkal, amelyek dimenzióját a k és n paraméterek határozzák meg. A sorok száma k, és az oszlopok száma n = k + m.
Az ilyen mátrixok által generált kódokat (n, k) kódoknak nevezzük, és a megfelelő mátrixok generátorok (generátorok, generátorok). A G generáló mátrix az Ikk információból és az Rkm mérőmátrixokból áll. Ez egy lineáris kód tömör leírása, és a kanonikus (standard) formában ábrázolható
Mint információs mátrix, célszerű egyetlen mátrixot használni, amelynek rangját az információs bitek száma határozza meg
Az azonosító mátrix sorai lineárisan független kombinációk (alapvektorok), vagyis a páros összegzésük a modulo két nem vezet nulla sorhoz.
Az alapmátrix sorai a korrekciós kód első k kombinációit reprezentálják, és a fennmaradó kódkombinációk úgy érhetők el, hogy összefoglalják e sorok két különböző kombinációját.
A kiegészítő mátrix Rkm oszlopai meghatározzák az ellenőrzések kialakításának szabályait. Az egységek száma minden sorban a mátrix hozzáadott meg kell felelniük a feltétellel r1 ³ d0 -1, de az egységek száma határozza meg a számát 2-modulusú összegző a kódoló és dekódoló, és több közülük, a bonyolultabb berendezés.
A G (7.4) kód generáló mátrixa lehet a forma
A kódolási folyamat a k-bit információs szavak - I és n-bites kódszavak - egyenkénti megfeleltetéséből áll,
Például: az I = [1 0 1 0] információs szó a következő kódszónak felel meg
Ebben az esetben, az információ rész változatlan marad, és a korrekciós bitek által meghatározott összeadásával modulo két sor az ellenőrzés mátrix, amelynek szám egybeesik a bitek száma egy információs egységet tartalmazó kódot.
A dekódoló folyamat meghatározza az információs kódszóhoz továbbított vett kódszó megfelelését. Ezt a H (n, k) ellenőrző mátrix segítségével végezzük.
ahol az Rmk T az átültetett ellenőrző mátrix (oszlopváltás sorok módosítása); Az Imm az azonosító mátrix.
A (7, 4) kód esetében az ellenőrző mátrixnak van az űrlapja
A G (n, k) és a H (n, k) között egyedülálló kapcsolat van, mivel ezeket az ellenőrzési szabályok szerint definiálják, míg a cH T = 0 kódszavaknak teljesülniük kell.
Az ellenőrző mátrix sorai meghatározzák az ellenőrzések kialakításának szabályait. A (7, 4) kód esetén
A kapott szindrómát a mátrix oszlopaihoz hasonlítjuk össze, és meghatározzuk a kibocsátást, amelyben a hiba történt, az oszlopszám megegyezik a hibás számjegy számával. A hiba kijavításához a hibabitet invertálni kell.
Példa 1. Hozzon létre egy olyan csoportkódot, amely képes az elsődleges ábécé 16 karakterének átvitelére egy hiba korrekciójával. Mutassa be a 1001 továbbított információs szó kódolását, dekódolását és hibajavítását.
1. G (n, k) generáló mátrixot hozunk létre.
Ha a kódtérfogat N = 2 k = 16, akkor az információs bitek száma k = 4. Egy hiba rögzítéséhez szükséges minimális kód távolság d0 = 2s + 1 = 3. Az információs szó adott hossza szerint a kapcsolatok segítségével:
n = k + m, 2 n ³ (n + 1) 2 k és 2 m ³ n + 1
számítsuk ki az n és az m kód alapvető paramétereit.
Honnan n = 7, azaz létre kell hozni a (7, 4) kódot.
Mivel az információs mátrix Ik (7, 4) - válassza ki az identitás mátrix (4'4), valamint Rkm (7, 4) ellenőrző mátrix - válaszd ki a mátrix (4'3), minden egyes sora, amely az egységek számát nagyobb vagy egyenlő, mint kettő (r1 £ d0-1).
Így, mint a generáló, tudjuk venni a mátrix
.
Információ a munkáról "Korrekciós kódok"
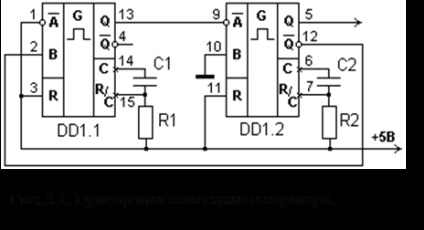
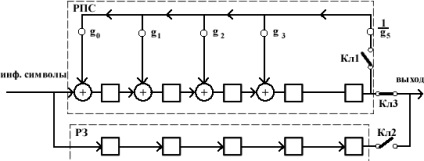
visszacsatolás nem az n-k eltolódásokon keresztül, hanem azonnal az első órajel ciklusából. Ez segít az információ és az ellenőrző szimbólumok közötti szakadék áthidalásában. Ábra. 1.1. Kódkapcsoló (n-k) - bites eltolási regiszter alapján ciklikus kódra. A kezdeti állapotban a K1 kulcs az 1. pozícióban van, és a K2 kulcs zárt. Az információs szimbólumok egyszerre működnek.
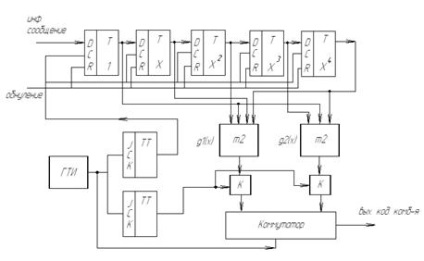
a maximális valószínűség módszerével, vagyis optimális módon. Az optimális dekódolás azt jelenti, hogy a dekóder több hibát rögzít, mint a küszöbérték. 2. A kódoló eszköz kifejlesztése konvolúciós kód kialakításához 2.1 A kódoló eszköz szerkezeti sémájának kialakítása konvolúciós kód létrehozásához A szerkezeti kód megépítésének alapja.
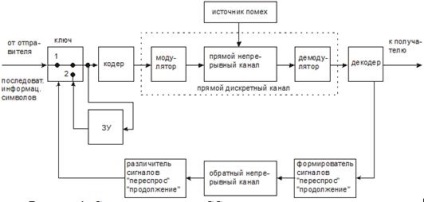
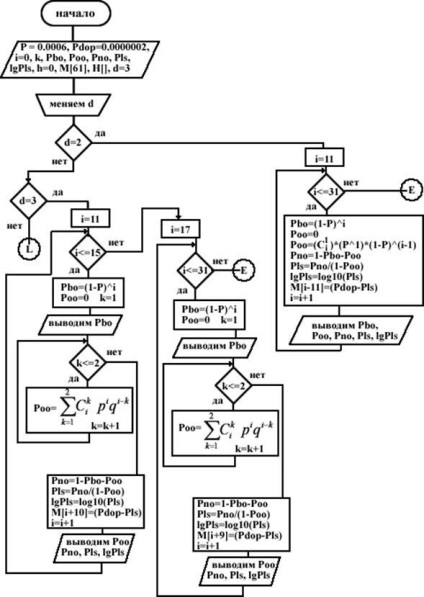
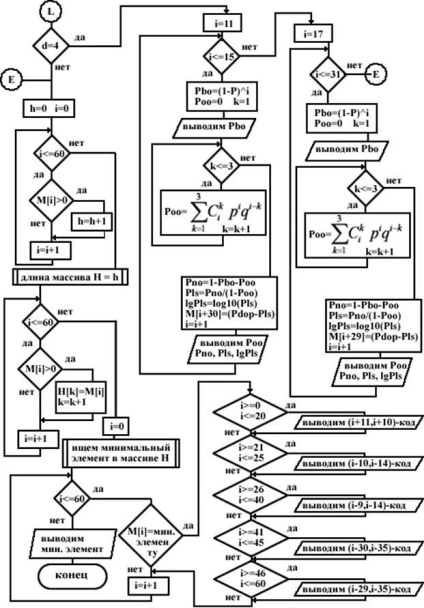
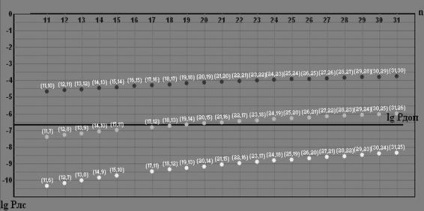
a következő adattömör memóriájából a következő rész nem kerül továbbításra, amíg erre a részre nem érkezik válasz. Számítási eljárás LLS és RLS például a számítást a gyűrűs (n, k) -code Hamming biztosító minimális különbség ROP - RLS (n, k): A számítás a (18,13) kód d = 3. Ehhez be kell mutatni a jelölést: · A Pbo a DSC kimenetén megjelenő kombináció valószínűsége.
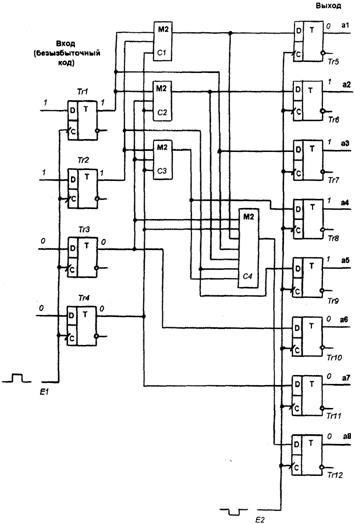
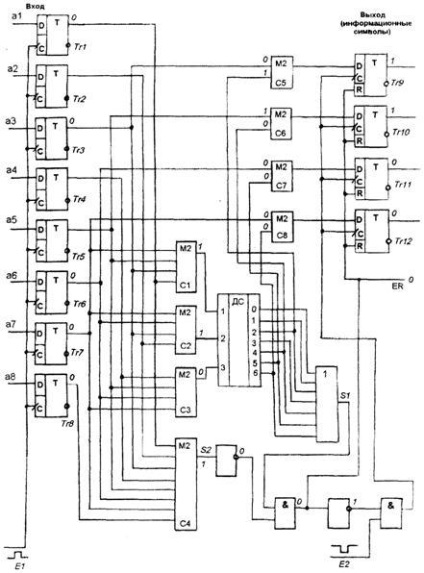
Egy másik: Megkaptuk a végleges szabályok megalkotásához a kódot korrigálni tudnak minden egyedi hibák és érzékeli kettős: A szabályok megalkotásához hibajavító kódot (*), akkor össze egy táblázatot a megengedett kombinációk kódját kötet 9 szó, hogy javítani tudja az összes egy- és kétágyas hiba észlelése. A "nem redundáns kód" oszlopban kilenc (kilenc) értéket írunk.