Egy komplex szám logaritmusa
Mivel a szinusz és a koszinusz nem függ a többszöggel
És ez az egyenlőség már nyilvánvaló, hiszen ez egy komplex szám trigonometrikus formája.
Így a logaritmus a sík minden pontján létezik, kivéve a nulla értéket. Valódi pozitív szám esetén az argumentum 0, így ez a végtelen pontkészletnek van formája. vagyis az egyik érték, nevezetesen, mikor. esik az igazi tengelyre. Ha kiszámítjuk a negatív szám logaritmusát, akkor kapjuk. azaz a pontok halmaza felfelé mozog, és egyik sem esik az igazi tengelyre.
A képletből kiderül, hogy az eredeti szám nullázó argumentuma esetén a logaritmus egyik értéke a valós tengelyre esik. És ez megfelel a megfelelő félértéknek, és ezért csak a pozitív számok logaritmusát vettük figyelembe az iskolai matematika során. A negatív és képzeletbeli számok logaritmusai is léteznek, de nincsenek értékük az igazi tengelyen.
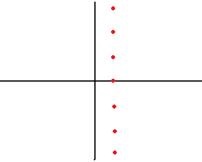
Az alábbi ábra azt mutatja, hogy hol helyezkednek el a síkban a pozitív szám logaritmusának összes értéke. Egyikük a valós tengelyen van, a többi pedig magasabb és alacsonyabb. . és így tovább. Negatív vagy komplex szám esetén az argumentum nem nulla, ezért a függőleges csúcssor függőlegesen elmozdul, aminek következtében egyetlen pont sem lesz a valós tengelyen.
A megoldás. Meghatározzuk egy szám (2-es érték) modulusát és a 180 0 argumentumot. Ezután =.

Függelék 1. Kérdések a bizonyítékok (jegyek).
1. Bizonyítsuk be az integrációt részekből.
1. Bizonyítsuk be, hogy a csere. ahol r = HOC (r1, rk) csökkenti a racionális frakció integrális integrálját.
2. Bizonyítsuk be, hogy egy csere cseréje a formanyomtatványt integrálva racionális frakcióba integrálja.
3. Derítsük ki a szinusz- és koszinusz-transzformációs képleteket
univerzális trigonometrikus helyettesítésre.
4. Bizonyítsuk be, hogy abban az esetben, ha a függvény páratlan a koszinusz vonatkozásában, a csere csökkenti az integrált értéket egy racionális frakcióra.
5. Bizonyítsuk be, hogy abban az esetben, ha
csere: csökkenti a racionális frakció integrálját.
6. Bizonyítsuk be, hogy az űrlap integráljára cserélje ki az integrált értéket a racionális frakcióval.
7. Bizonyítsd be a képletet!
8. Bizonyítsuk be, hogy az űrlap integráljára az integrált értéket racionális törtrész váltja fel.
9. Bizonyítsuk be, hogy a forma szerves részét képező csere csökkenti a racionális frakció integrálját.
1. Bizonyítsuk be, hogy a függvény a függvény antiderivatívja.
2. Mutassa be a Newton-Leibniz-formulát :.
3. Bizonyítsuk be a kifejezetten meghatározott görbe hosszának képletét:
4. Bizonyítsd be a polárkoordinátákban megadott görbe hosszának képletét
Bizonyítsd be a tételt: konvergál. konvergál.
1. Határozzuk meg a kifejezetten meghatározott felület területére vonatkozó képletet.
2. A képletek a poláris koordinátákra való áttéréshez.
3. A polar koordináták Jacobi determinánsának származtatása.
4. Az átmeneti képletek hengeres koordinátákra történő származtatása.
5. A hengeres koordináták Jacobi determinánsának származtatása.
6. A szférikus koordinátákra való áttérésre szolgáló képletek származéka:
1. Bizonyítsuk be, hogy a helyettesítés csökkenti a homogén egyenletet egy elválasztó változóval.
2. Végezze el a lineáris homogén egyenlet megoldásának általános formáját.
3. A lineáris inhomogén egyenlet megoldásának általános formáját a Lagrange módszerrel kell előidézni.
4. Bizonyítsuk be, hogy a helyettesítés csökkenti a Bernoulli egyenletét lineáris egyenletre.
1. Bizonyítsuk be, hogy a helyettesítés csökkenti az egyenlet sorrendjét k-vel.
2. Bizonyítsuk be, hogy a csere egyenként csökkenti az egyenlet sorrendjét.
3. Tételezzük fel a tételt: egy függvény egy lineáris homogén differenciál egyenlet megoldása egy jellegzetes gyökér.
4. Bizonyítsuk be, hogy a lineáris homogén differenciálódás lineáris kombinációja. az egyenletnek is van megoldása.
5. Bizonyítsd be a megoldások bevezetésének tételét: Ha a jobb oldali lineáris inhomogén differenciálegyenlet megoldása. Az a megoldás ugyanaz a differenciálegyenlet, de a jobb oldali. akkor az összeg a jobb oldali egyenlet megoldása.
1. Tételezzük fel, hogy a függvényrendszer lineárisan függ.
2. Tegyen egy tételt n lineáris homogén differenciálegyenlet n lineárisan független megoldásainak létezéséről n.
3. Bizonyítsuk be, hogy ha 0 a sokféleség gyökere. akkor a gyökérnek megfelelő megoldások rendszere formában van.
1. Bizonyítsuk be, hogy az exponenciális formát alkalmazzuk, hogy a komplex számok szorzása megszorozza a modulokat, és az argumentumok összeadódnak.
2. Mutassuk meg a Moivre képletet az n fokozatra
3. Bizonyítsuk be egy komplex szám n-edik gyökér képletét
4. Bizonyítsuk be, hogy u
a szinusz és koszinusz generalizációi, azaz Valódi számok esetén ezek a képletek szinuszot (koszinuszt) eredményeznek.
5. Bizonyítsuk be a komplex szám logaritmusának képletét:
Kisebb és szóbeli kérdések az elméletről (kollokviumok esetében).
1. Mi a primitív és határozatlan integrál, mi más?
2. Magyarázza el, miért is ellentmondásos.
3. Írja be az integrációs képletet részekre.
4. Milyen fajta csere szükséges a faj integrálódásában, és hogyan szünteti meg a gyökereket?
5. Írja le az integrált és a racionális frakciók bomlásának formáját protozoákra, abban az esetben, ha minden gyökér különálló és valós.
6. Írja le a racionális frakciók integrandusának bomlásának formáját protozoára, abban az esetben, ha minden gyökér valódi, és van egy többszörös gyökere a k-nek.
1. Írja le a racionális frakció legegyszerűbb frakciókra való bomlását abban az esetben, ha a nevező 2 fokos tényezővel rendelkezik a negatív diszkriminanciával.
2. Milyen csere csökkenti a racionális frakció szerves részét?
3. Mi az univerzális trigonometriai helyettesítés?
4. Milyen helyettesítéseket végeznek azokban az esetekben, amikor az integrált jel alatt szereplő funkció páratlan a szinusz (koszinusz) tekintetében?
5. Milyen szubsztitúciókat végeznek az integrandumban lévő kifejezések jelenlétében. . vagy.
1. Határozott integráció meghatározása.
2. Soroljon be egy meghatározott integrál alapvető tulajdonságait.
3. Írja le a Newton-Leibniz képletet!
4. Írja be a forradalom testének a képletét.
5. Írjon egy képletet egy kifejezetten meghatározott görbe hosszára.
6. Írjon egy képletet a paraméteresen meghatározott görbe hosszára.
1. A helytelen integrál meghatározása (határértékkel).
2. Mi különbözteti meg az 1-es és a 2-es típusú nem megfelelő integrálokat?
3. Adjon egyszerű példákat az 1. és 2. típusú konvergens integrálokra.
4. Milyen konvergencia az integrál (T1).
5. Mivel a konvergencia kapcsolódik az antiderivatív (T2) véges határához,
6. Mi a szükséges jel a konvergencia, annak megfogalmazása?
7. Az összehasonlítás jele a végleges formában
8. Az összehasonlítás tünete a korlátozó formában.
9. Többszörös integrál meghatározása.
1. Módosítsa az integráció sorrendjét, a legegyszerűbb példában.
2. Írja be a felületi terület képletét.
3. Mik azok a poláris koordináták, írja át az átmeneti képleteket.
4. Mi a poláris koordinátarendszer Jacobiája?
5. Mik a hengeres és a gömb alakú koordináták, mi a különbség.
6. Mi a hengeres (gömb alakú) koordináták Jacobiája?
1. Mi az 1. sorrend különbségi egyenlete (általános forma).
2. Mi az 1-es sorrendű differenciálegyenlet, amelyet a származék tekintetében oldott meg. Adjon példát.
3. Mi az elválasztható változókkal rendelkező egyenlet.
4. Mi az általános, konkrét megoldás, a Cauchy-feltételek.
5. Mi a homogén egyenlet, mi a megoldás általános módja.
6. Mi a lineáris egyenlet, mi a megoldás algoritmusa, mi a Lagrange módszer.
7. Mi a Bernoulli-egyenlet, a megoldás algoritmusa.
1. Milyen helyettesítésre van szükség egyfajta egyenlethez.
2. Milyen helyettesítésre van szükség egyfajta egyenlethez.
3. Mutassa be példákkal, hogyan lehet kifejezni az űrlapot.
4. Mi a lineáris differenciálegyenlet n.
5. Mi a jellemző polinom, a jellemző egyenlet.
6. Formázzunk egy olyan tételre vonatkozó tételt, amelyre a megoldás egy lineáris homogén differenciálegyenlet.
7. Tételezzük fel, hogy a lineáris homogén egyenlet lineáris kombinációjának megoldása is megoldást jelent.
8. Hozzon létre egy tételt a megoldások és következményeinek kivetéséről.
9. Mi a lineárisan függő és lineárisan független funkcionális rendszer, adjon néhány példát.
10. Mi a meghatározó a Vronsky rendszerben n funkciók, példát mutatnak a Vronsky determináns LZS és LNS rendszerek.
1. Mi a tulajdonsága a Wronskian meghatározónak, ha a rendszer lineárisan függ.
2. Hány, lineárisan homogén differenciálegyenlet lineárisan független megoldása létezik.
3. Az FSS (alapvető megoldási rendszer) definíciója egy lineáris homogén egyenlet n.
4. Hány funkció szerepel az FSR-ben?
5. Írja le az egyenletrendszer formáját a Lagrange-módszer megtalálásához n = 2-re.
6. Írja le az adott megoldás formáját abban az esetben, amikor
7. Mi a differenciálegyenletek lineáris rendszere, írj egy példát.
8. Mi a differenciálegyenletek autonóm rendszere?
9. A differenciálegyenletek rendszerének fizikai jelentése.
10. Írja le, hogy az egyenletek rendszere milyen funkciókat tartalmaz, ha ismeretesek a rendszer mátrixának sajátértékek és sajátvektorok.
1. Mi a képzeletbeli egység?
2. Mi a konjugált szám, és mi fog történni, amikor az eredeti számmal megszorozódik.
3. Mi a komplex szám trigonometrikus, exponenciális formája.
4. Írja be az Euler képletet.
5. Mi a modul, egy komplex szám érve.
6. Mi történik a modulok és érvekkel, amikor megszorozzák (osztják)?
7. Írja be a Moivre képletet az n fokozatba.
8. Írja be a n.
9. Írja be az általánosított szinusz és koszinusz képletét egy összetett argumentumra.
10. Írja be a komplex szám logaritmusának képletét.
3. függelék Előadások feladata.