A 11. téma a termodinamika második törvénye
Cél: megérteni a termikus hatékonyság fogalmának lényegét, Carnot elméleti ciklusait és a termodinamika második törvényének lényegét.
A termodinamika második törvényének fő rendelkezései, az energia megőrzésének és átalakításának egyetemes törvényének egyike, azt állítja, hogy a hő átalakítható munkává és hővé, anélkül, hogy meghatározta azokat a feltételeket, amelyek között ezek az átalakulások lehetségesek.
Teljesen nem veszi figyelembe a termikus folyamat irányát, és nem ismeri ezt az irányt, nem tudja megjósolni természeteit és eredményeit.
Például az első törvény nem oldja meg azt a kérdést, hogy a fűtött testről a hidegre vagy fordítva történik-e hőátadás. A mindennapos megfigyelések és kísérletek azt mutatják, hogy maga a hő csak a fűtött testektől a hidegebbé válik. A fűtött testből a tápközegbe történő hőátadás mindaddig megtörténik, amíg a környező táptalaj teljes termál egyensúlyba nem kerül. Csak a munkaköltségek árán változtathatja meg a hőmozgás irányát.
A hő tulajdonsága élesen megkülönbözteti a munkától.
A munka, mint minden más típusú energia, minden folyamatban könnyen és teljesen hővé válik. A munkának hőre való teljes átalakítása az ősidőkben ismert volt az embernek, amikor két darab fa dörzsölésével tüzet húzott ki. A munka hővé alakításának folyamata folyamatosan zajlik a természetben: súrlódás, ütés stb.
A hõ teljesen más módon viselkedik, például a termikus gépekben. A hő átalakulása a munkába csak a hőforrás és a hővivő közötti hőmérsékletkülönbség jelenik meg. Ezzel a hőt nem lehet munkába állítani.
Az említettekből következik, hogy mély különbség van a hő munka és hátra történő átalakítása között. Az a törvény, amely lehetővé teszi a hőáramlás irányának meghatározását és a hőnek a termikus gépekben történő hőátadáshoz szükséges maximális határérték meghatározását, a tapasztalatból származó új törvény. Ez a termodinamika második törvénye, amely minden tipikus folyamathoz közös jelentéssel bír, a termodinamika második törvénye nem korlátozódik a mérnöki keretrendszerre; a fizika, a kémia, a biológia, a csillagászat stb.
1824-ben Sadi Carnot, francia mérnök és tudós, a tűz hajtóerejéről folytatott vitáján a második törvény lényegét tárta fel. Azt írta: "Bárhol van hőmérséklet-különbség, egy hajtóerő fordulhat elő. A hő hajtóereje nem függ a kifejlesztett anyagoktól: mennyiségét kizárólag a testek hőmérséklete határozza meg, amelyek között végső soron a hő átvitelére kerül sor. A gáz hőmérsékletének kezdetben a lehető legnagyobbnak kell lennie annak érdekében, hogy a hajtóerő jelentős fejlődését érje el. Ugyanezen okból a lehető legnagyobb mértékben kell hűteni. Nem lehet reménykedni, legalábbis valaha, hogy gyakorlatilag kihasználja az üzemanyag teljes hajtóerejét. "
A múlt század 50-es éveiben Clazius a termodinamika második törvényének legáltalánosabb és legmodernebb megfogalmazását adta a következő posztulátumnak: "A hő nem tud átmenni egy hideg testről egy fűtött ajándékfolyamathoz (kompenzáció nélkül)."
Clausius posztulátumát a környező természet megfigyeléseiből származó kísérleti törvénynek kell tekinteni. Clausius következtetése a technika területén történt, de kiderült, hogy a fizikai és kémiai jelenségekről szóló második törvény is helyes. Clausius posztulátuma, mint a második törvény minden más megfogalmazása, a természet egyik alapvető, de abszolút törvényét fejezi ki, hiszen a körülöttünk lévő földi körülmények között véges méretű tárgyakra formált.
A Clausius 1851-ben egyidejűleg a Thomson a termodinamika második törvényének másik megfogalmazását fejezte ki, amelyből következik, hogy nem minden hőtől érkező hő juthat munkába, csak néhányat. A hő egy részét át kell engedni a hűtőbordába.
Ezért a munka megszerzése érdekében olyan hőforrásra van szükség, amelynek magas hőmérséklete van, vagy hűtőborda, valamint hőforrás alacsony hőmérsékleten vagy hűtőbordában. Ráadásul Thomson álláspontja azt mutatja, hogy nem lehet olyan örök mozgatógépet felépíteni, amely csak a tengerek, az óceánok, a levegő belső energia felhasználásával hozna létre munkát. Ez a rendelkezés a termodinamika második törvényeként fogalmazható meg: "A második faj állandó mozgását lehetetlen megvalósítani". A második faj örökös mozgása alatt olyan motor van, amely képes teljesen megfordítani a munkát az egyetlen forrástól kapott hőnek. A fentieken túlmenően a termodinamika második törvényének több olyan összetétele is létezik, amelyek lényegében nem vezetnek be semmi újat, ezért nem adják meg.
2 Hőhatékonyság és hűtési együttható.
Az egy ciklusban a pozitív munkára átfordított hőmennyiségnek a munkaközeghez adott teljes hőmennyiséghez viszonyított hányadának a hőtényezőjét nevezik hatékonyságnak.
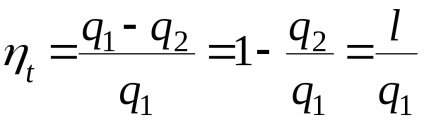
A hatékonysági érték a hőgépciklus tökéletességének jelzője. Minél nagyobb a hatékonyság, annál több a hő bemenet hasznos része. A ciklus termikus hatékonysága mindig <1,и мог бы быть равен 1, если бы q1=

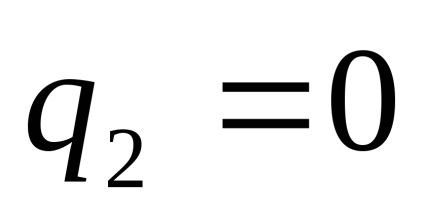
3 Carnot tétele: "Zárt körkörös eljárásban a hő csak mechanikai munkákra szállítható, csak a hőelvezetők és a hőcserélők közötti hőmérsékletkülönbség jelenlétében. Minél nagyobb ez a különbség, annál nagyobb a hőmotor ciklusának hatékonysága. "
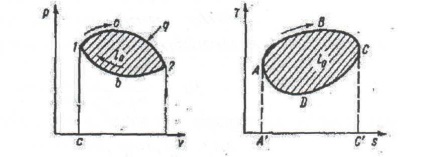
4.1 ábra - A hőmotor körkörös ciklusa
A munkatermék bõvítése alacsonyabb hõmérsékleten történik, mint a sajtolás, és a bõvítõ munka kisebb, mint a sajtolás. Ez a folyamat csak a külső munka költségeivel hajtható végre.
A hővevőkészülékek fordított ciklusában rt-re kerül. specifikus hőt
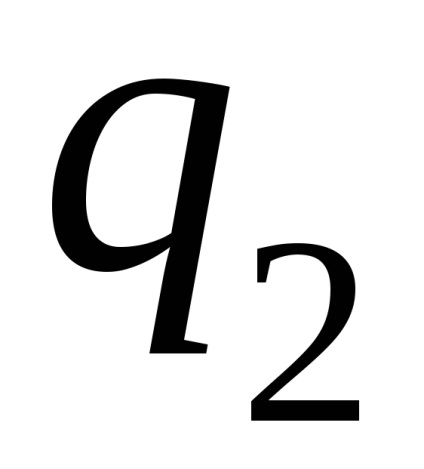
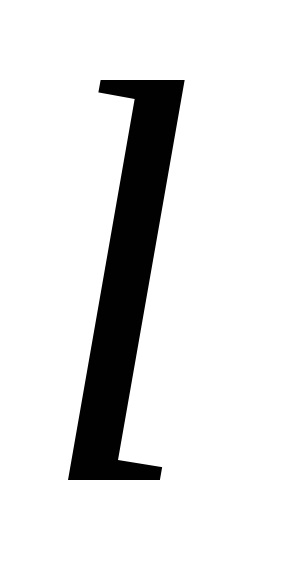
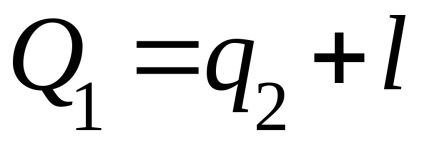
A fordított ciklus tökéletességének mértékét az ún. a ciklus hűtési együtthatója.
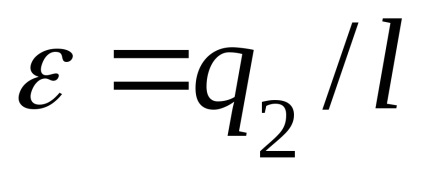
4 Közvetlen Carnot reverzibilis ciklus.
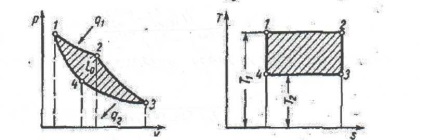
4.3. Ábra - Közvetlen Carnot ciklus
2 adiabatból és 2 izotermából áll. Először is, az izotermikus tágulási folyamat során a hő visszavezethetővé válik a rt-be. egy állandó hőmérsékletű hűtőbordából. Ezután a reverzibilis adiabatikus expanziós folyamat során a hőmérséklet rt ↓ a hővivő hőmérsékletére. Továbbá a reverzibilis izotermikus folyamatban a hővevõ hõmérsékletén a hõt eltávolítják a rt-bõl. neki. A zárási folyamat egy adiabatikus folyamat, amelyben a rt. ↑ a kezdeti és a r.t. visszatér eredeti állapotához.
A rt. Teljes ciklusára egy bizonyos mennyiségű q1 hőt jelentettek a hűtőbordából, és egy q2 specifikus mennyiséget irányították át a hővevőkészülékre.
Ennek és mindkettőnek
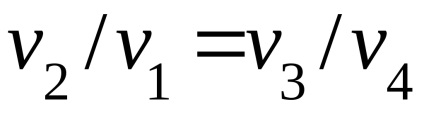
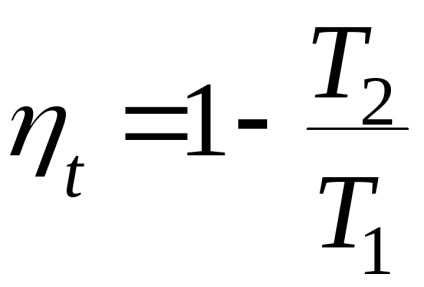
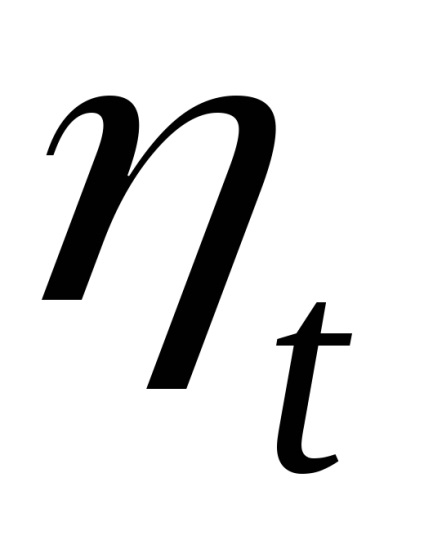
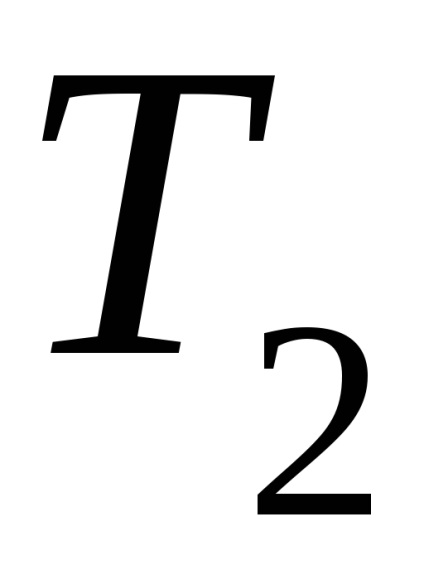
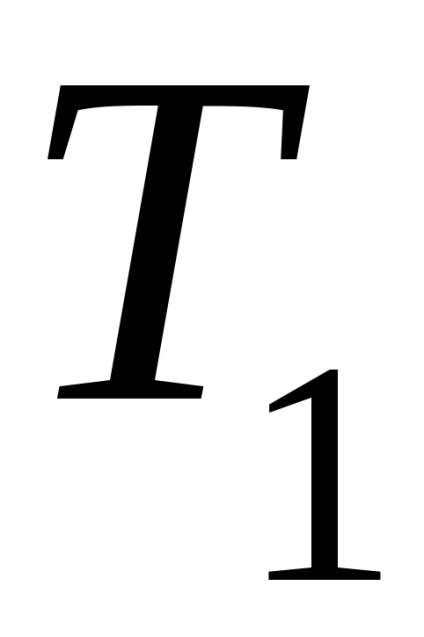
2.
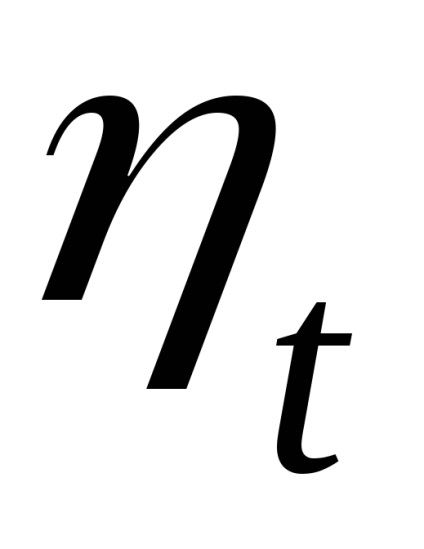
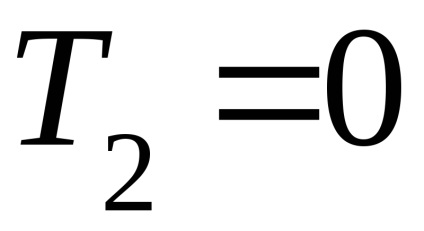
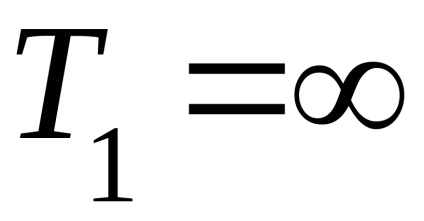
3.
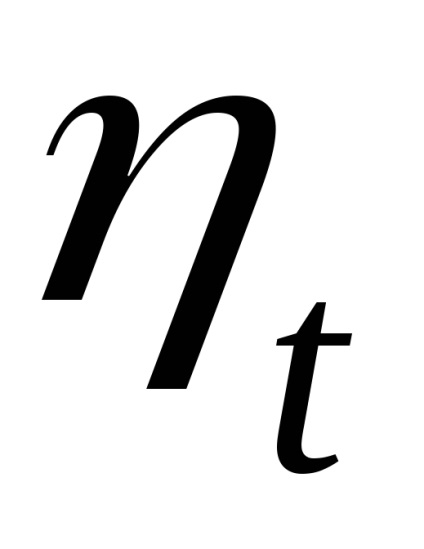
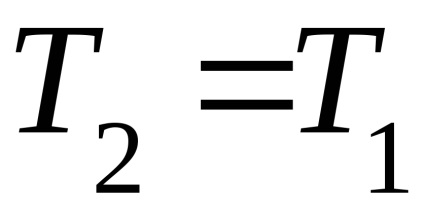
4.
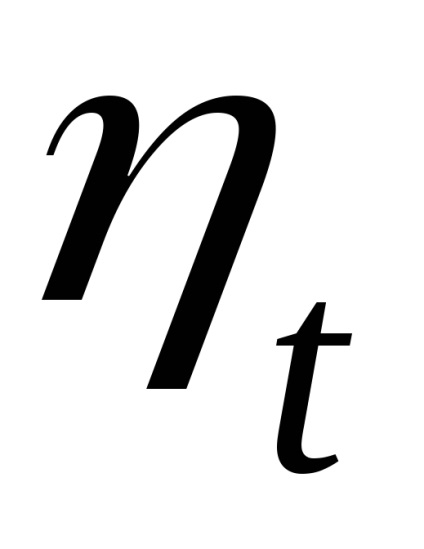
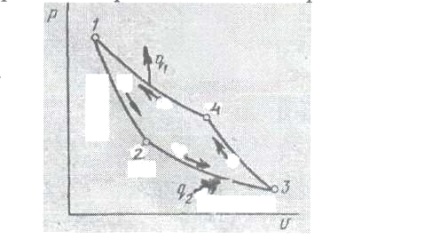
4.4. Ábra - Carnot fordított ciklus
A Carnot ciklus nem csak előre, hanem ellenkező irányban is áramlik. A fordított ciklusban működő gépet hűtőgépnek nevezik. A kezdeti 1-es ponttól kezdve a PT kiterjed az adiabat (1-2) mentén, és ebben az esetben
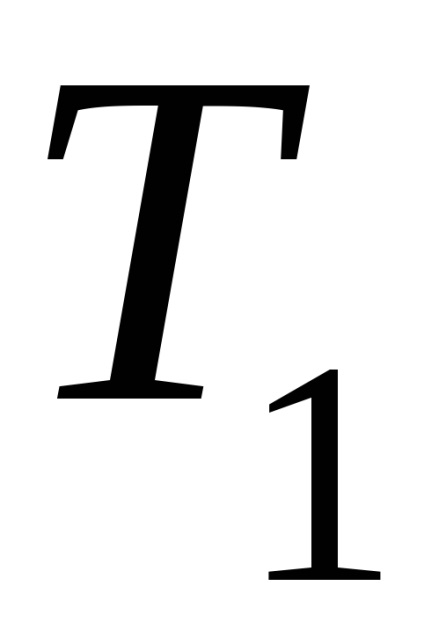
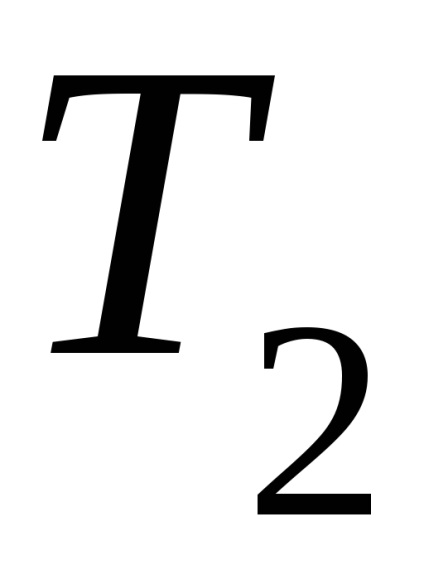
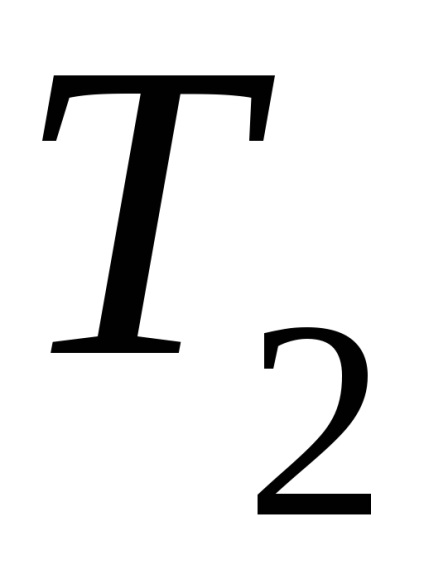
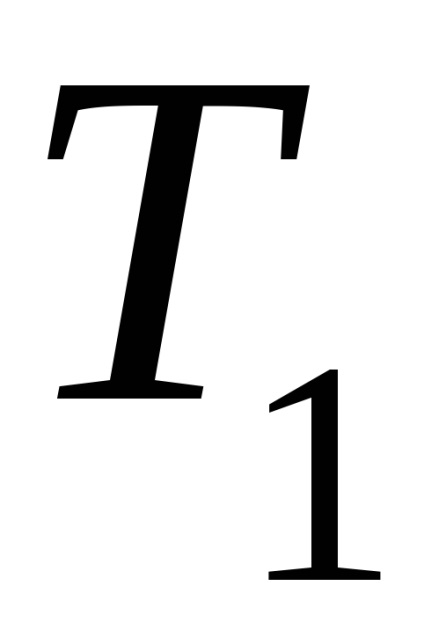
5 A termodinamika második törvényének matematikai kifejezése
Tekintsük külön a második törvény kifejeződését a reverzibilis és visszafordíthatatlan ciklusokra vonatkozóan.
Reverzibilis ciklusok esetén:
A hatékonyság kifejezéséből következik
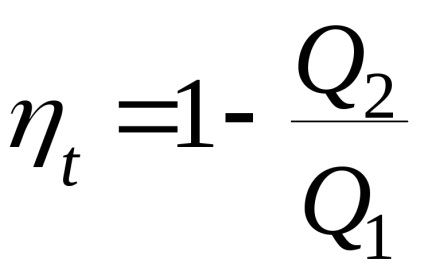
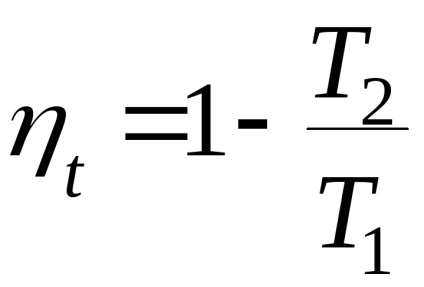
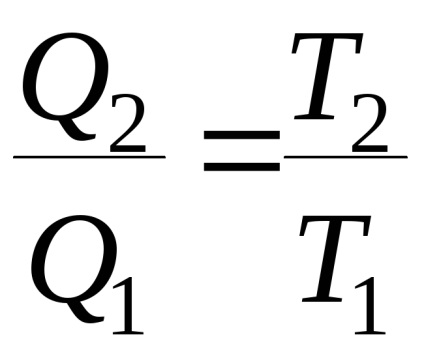
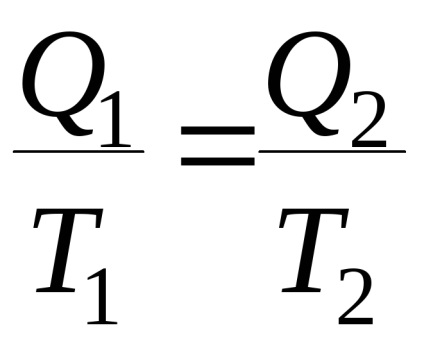
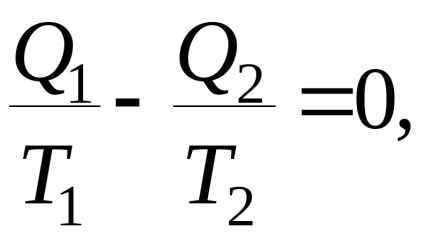
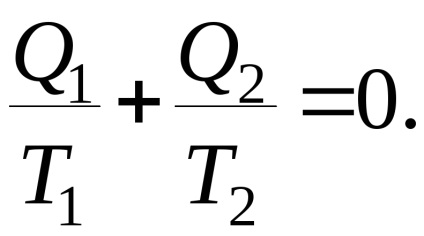
Ez a kimenet bármilyen ciklusra használható. Ezt a ciklust adiabatusokkal egy végtelen nagy számú elemi ciklusra osztjuk, és minden ciklus elemi Carnot ciklusnak tekinthető. A (4.1) egyenlet minden elemi ciklusra és az egész önkényes ciklusra érvényes
A Clausius által kiváltott egyenlet (4.2.) A termodinamika második törvényének matematikai kifejezését jelenti, és az első Clausius integrálnak nevezik.
Visszafordíthatatlan ciklusok esetén:
Figyelembe kell venni, hogy egy visszafordíthatatlan ciklus hatékonysága mindig kisebb, mint a reverzibilis ciklus, azaz
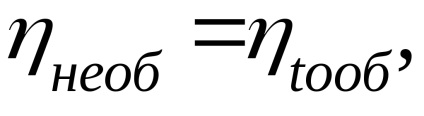
ezért
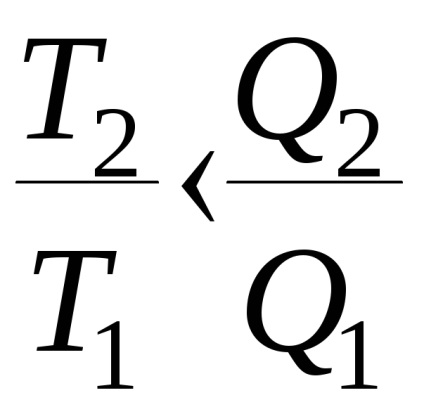
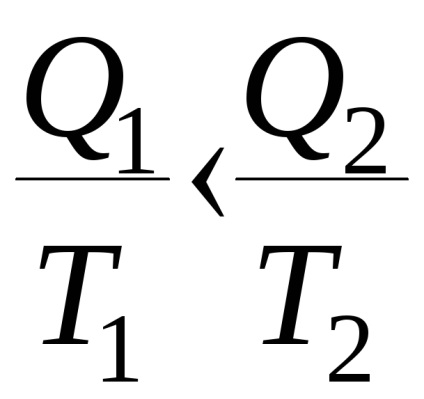
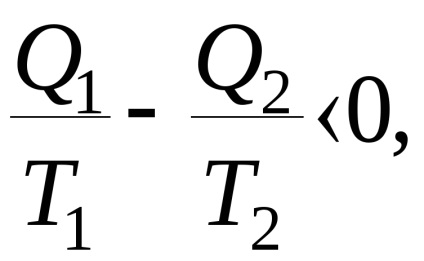
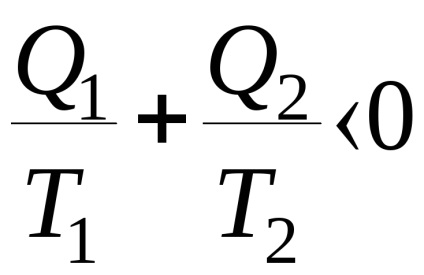
Az utolsó egyenletből következik, hogy az algebrai hő kevesebb, mint nulla vagy
Ez a kimenet bármilyen ciklusra használható. Ezt a ciklust adiabatusokkal egy végtelen nagy számú elemi ciklusra osztjuk, és minden ciklus elemi Carnot ciklusnak tekinthető. A (4.3) egyenlet mindegyik elemi ciklusra és az egész önkényes ciklusra vonatkozik
A Clausius által kiváltott (4.4) egyenlet a termodinamika második törvényének matematikai kifejeződését és az első Clausius-integrálnak nevezzük.
Egyesítjük az egyenleteket (4.2.) És (4.4.), És megkapjuk
A (4.5) egyenlet a termodinamika második törvényének általános kifejezése. Az egyenlőségi jel a reverzibilis ciklusokra, az egyenlőtlenségekre pedig az irreverzibilis ciklusokra utal.
1. Mi a termodinamika második törvénye?
2. Mi a termikus hatásfok?
3.Milyen a hűtési együttható?
4. Mit jelent a Carnot-tétel?
5. Milyen folyamatok a közvetlen Carnot ciklus?
6. Milyen folyamatok állnak a fordított Carnot ciklusból?
7. Miért nem lehet több egy hőhatás?
8. Ismertesse Clausius első integrálját?
9. Mutassa be Clausius második integrálját?
10. Mi a hő?