Jelek és interferencia véletlenszerű folyamatokként - stadopedia
A fizikai folyamatok sokfélesége (különböző fizikai mennyiségek időbeli változása, beleértve az elektromos kommunikációs jeleket is), amelyek a mindennapi életben teljesíthetők, két osztályra oszlik.
Az első osztály olyan folyamatokat foglal magában, amelyek előrehaladása előre megjósolható, és a priori [2] információkkal rendelkezik. Például az ilyen folyamatok csak teljesen elszigetelt fizikai rendszerekben keletkezhetnek, ahol nem veszi figyelembe a környezet hatását. Az ilyen folyamatokat determinisztikusnak hívják.
A második osztály olyan folyamatokból áll, amelyeknek menetét nem lehet az idő rendszeres funkciójaként leírni. Bármely adott pillanatban a folyamat bizonyos valószínűséggel bizonyos kvantitatív értéket vehet fel a lehetséges csoportokból. Tekintsünk egy példát. Ismert, hogy még a rádiócsövek elektródáinál állandó potenciálkülönbség mellett az anódáram kaotikus rezgése is megfigyelhető, amelyet a katódból az anódba áramló elektronáram intenzitásának ingadozása okoz. Ezt a jelenséget lövésnek nevezzük, és az anódáram indukált ingadozása a véletlenszerű eljárás tipikus példája. Ebben az esetben nem lehet előzetesen meghatározni az eljárás folyamatát egy determinisztikus idő függvényében. Csak az egyes időponthoz tartozó folyamatértékek valószínűségi eloszlását határozhatja meg.
Egy véletlenszerű X (t) eljárás egy olyan speciális függvény, amelyet az jellemez, hogy bármikor t az értékek véletlenszerű változók.
A véletlen folyamat konkrét folyamatát, amelyet bármely különleges élmény eredményeként hoztak létre, az úgynevezett megvalósítása.
Az egyes megvalósítások dimenziója meghatározza a véletlen folyamat egészének méretét.
Elképzelni, hogy egy görbe véletlenszerű folyamata nem lehetséges, de néha olyan gráfot használ, amelyen a folyamat több megvalósítását a lehetséges esetek számáról készítik (1. ábra).
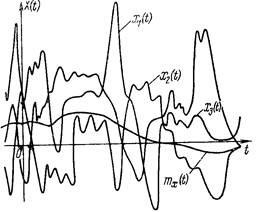
Ábra. 1. A folytonos véletlenszerű X (t) és a matematikai várakozás mx (t)
t0 időpillanatot, majd a véletlen értékét
folyamat ebben az időben egy véletlen változó, amelyet a folyamat t0 pontjában a keresztmetszetnek nevezünk.
Egy véletlenszerű jel pillanatnyi értékeinek rögzítése egy bizonyos időintervallumban csak a véletlenszerű folyamat egyetlen megvalósítását eredményezi. A véletlenszerű folyamat az ilyen megvalósítások végtelen gyűjteménye, amely statisztikai egységet képez. Például az együttes az x1 (t), x2 (t) jelek halmaza.>, Ami egyidejűleg megfigyelhető a teljesen azonos zajfeszültség-generátorok kimenetén.
Nem feltétlenül szükséges, hogy egy véletlen folyamat megvalósulását olyan összetett viselkedésű funkciók képviselik, amelyek idővel szabálytalanok. Gyakran kell vizsgálni a véletlenszerű folyamatokat, amelynek kialakításához, például, mindenféle harmonikus jelek U cos (wt + j), ahol az egyik a három paraméterek U, W, J - egy véletlen változó vesz bizonyos értékeket minden megvalósításában. Az ilyen jel véletlenszerű jellege abban rejlik, hogy nem lehet előre tudni e paraméter értékét.
A véges számú paramétertől függő realizációkon alapuló véletlenszerű folyamatokat általában kváziderminisztikus véletlenszerű folyamatoknak nevezzük.
Különböző, összekapcsolt jelek, amelyek a különböző üzenetek hordozói, véletlenszerű folyamat megvalósítását jelentik.
A véletlenszerű folyamat a kommunikációs csatornában zavar (zaj). Ezért a jelek, az interferencia és az üzenetek továbbításában való kölcsönhatásuk, valamint az átviteli folyamat kutatása és a különféle kommunikációs rendszerek objektív értékelése céljából további vizsgálatra van szükség a véletlen folyamatok elméletének módszerével.
A kvantitatívan véletlenszerű eljárást az X (t) idő véletlenszerű függvénye írja le, amely bármikor eltérő értékeket vehet fel egy adott valószínűségi eloszlással.
Attól függően, hogy az X argumentum (t időpont) és a véletlenszerű X folyamat megvalósításának milyen értékei, attól függően, hogy milyen véletlenszerű folyamatok négy típusát különbözteti meg.
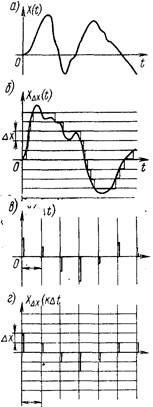
Folyamatos véletlenszerű eljárás: t és X bármely értéket vehet fel a valós tengely szegmensén (vagy talán egészében).
A diszkrét véletlen folyamat: t folyamatos, X értéke pedig diszkrét (a lehetséges értékek egyikét Dx lépéssel).
Egy folytonos véletlen sorrend: t diszkrét (Dt lépéssel), és az X bármelyik értéket a numerikus tengely szegmensére (vagy egészére) vehet fel. Az ilyen folyamatokat gyakran diszkrét időfolyamatoknak is nevezik.
A különálló véletlen szekvencia [3]: t és X diszkrét.
Négy osztály megvalósításának példái a 3. ábrán láthatók. 2.
Véletlenszerű eljárás meghatározásához ismerni kell a funkcióját és a valószínűségi eloszlási sűrűséget.