Háromszög oldalai és szögei közötti korreláció
A háromszögben oldalai és szögei között vannak bizonyos kapcsolatok. Ha a háromszög bármelyik sarkája nagyobb, mint a másik, akkor az ezzel ellentétes oldal hosszabb, mint a másikhoz képest. Más szóval, a háromszög legnagyobb szöggel szemben a legnagyobb oldal, a középső szöggel szemben a középső oldal, a legkisebb sarokkal szemben a legkisebb oldal.
Világos, hogy ha egy háromszög szöge egyenlő, akkor az oldalak, amelyekkel szemben állnak, egyenlőek.
A háromszög oldalainak és szögeinek arányára vonatkozó tétel megfogalmazásához a következőket alkalmazhatjuk: a nagyobb szögben lévő háromszögben a nagyobb oldali oldal helyezkedik el. Azonban megfogalmazhatjuk a beszélgetést: a nagyobb oldalon lévő háromszögben nagyobb a szög.
Egy közvetlen tételben ismerjük a szögek méreteit, és ebből számolunk be az oldalak méretéről. És a fordított tételben ismeretesek az oldalak méretei, és következtetéseket vonnak le a szögméretekről. Ez azt jelenti, hogy egy közvetlen tétel igazolásakor szögek korrelációját adjuk meg, és a képarány igazolására van szükség. Az inverz - tekintettel a képarányra - bizonyítani kell a szögek korrelációját.
Hadd mutassunk be egy közvetlen tételt. Adjuk meg, hogy ΔABC esetén az A szög kisebb, mint a B szög (∠A <∠B, или ∠BAC <∠ABC). Требуется доказать, что сторона, лежащая напротив ∠A, меньше, чем сторона, лежащая напротив ∠B.
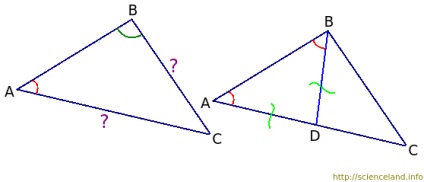
Ellentétben ∠A a BC oldallal, és a ∠B oldalával szemben az AC oldallal van. Kell bizonyítani, hogy BC A AB oldalán az AB oldalán egy ∠A-val egyenlő szöget állítunk be. Nyilvánvaló, hogy ez a szög kisebb, mint az ABC háromszög ∠B, mivel a ∠A hipotézis szerint <∠B. Мы откладывали новый угол внутри ∠B, а значит полученная сторона нового угла пройдет внутри ∠B и пересечет сторону AC в некой точке. Назовем эту точку D. Таким образом, мы получили ∠ABD, который равен ∠A. Mivel ∠A = ∠ABD, akkor a ΔABD isosceles. Az ő oldala AD egyenlő a BD oldalával. Az AC oldal két részből áll - AD és CD: AC = AD + CD. De mivel AD = BD írhatunk AC = BD + CD-t. Most vegye figyelembe a ΔBCD-t. Ebben, a BD és a CD két oldal. A harmadik fél BC. Mint a háromszög egyenlőtlenségi tételből ismert, bármely oldala kisebb, mint a másik kettő összege. Vagyis BC Ezért BC