A dichotómiás módszer - stadopedia
A nemlineáris egyenlet általános formája:
ahol az f (x) függvény definiált és folyamatos egy véges vagy végtelen intervallumon belül [a, b].
Minden olyan számot, amelyik f (x) nullára térképezi, az (1) egyenlet gyökere. A nemlineáris egyenleteket algebrai és transzcendentális egyenletekre osztják.
Az (1) egyenlet algebrai, ha az f (x) függvény algebrai. Az (1) egyenletet transzcendentálisnak nevezzük, ha az f (x) függvény nem algebrai.
Az (1) egyenlet megoldása a következőket jelenti:
1) meghatározza, hogy az egyenletnek gyökerei vannak-e.
2) meghatározza a gyökerek számát.
3) meg kell találni a gyökér értékét egy adott pontossággal.
Az első két szakasz a gyökerek szétválasztása. A gyökerek elválasztása az a módszer, amely olyan szegmenseket keres, amelyeken az (1) egyenletnek csak egy gyökere van. A legtöbb esetben a gyökerek szétválasztása grafikusan elvégezhető. Ehhez elegendő az F (x) függvény grafikonjának megrajzolása és azon szegmensek meghatározása, amelyeken az F (x) függvénynek csak egy metszéspontja van az abszcissza tengellyel (izolációs intervallumok).
Az izolációs intervallumok meghatározása után különböző gyökér finomítási módszereket alkalmaznak.
A gyökér finomításának módszerei
Úgy véljük, hogy az (1) egyenlet gyökereinek szétválasztását elvégezzük, és az izolációs szegmenst [a, b] egy gyökér helyezkedik el, amelyet finomítani kell az e hibával (1.
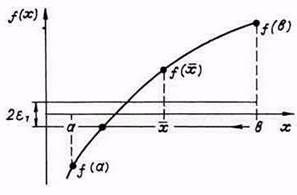
2. ábra: Dichotomy módszer
A dichotómiás vagy félosztásos módszer a következő. Határozza meg a szegmens közepét [a, b]. és kiszámítja a funkciót. Ezután választjuk ki, hogy a szegmens két részének melyik része legyen a gyökér további finomításához. Ha az f (x) egyenlet bal oldala az x argumentum folyamatos függvénye. akkor a gyökér a szegmens felében lesz, amelynek végein f (x) különböző jelekkel rendelkezik. Az 1. ábrán. 3 ez lesz az [a,], azaz a [a] intervallum. a finomítás következő lépésénél a b pontot a szegmens közepére mozgatjuk, és folytatjuk a megosztás folyamatát, mint a kezdeti szegmensben [a, b].
Az iteratív (ismétlődő) folyamat addig folytatódik, amíg az [a, b] intervallum kisebb lesz, mint az e megadott hiba:
vagy ha az f (x) függvény értékei (maradék) nem válnak elég kicsivé