Módszer nyomaték pont

Kezdőlap | Rólunk | visszacsatolás
A gazdaságok statikájának fő feladata olyan számítási módszerek alkalmazása, amelyek kiküszöbölik a közös egyenletrendszer megoldását.
A pillanatnyi pontok módszere a legegyszerűbb formában olyan gazdaságokra vonatkozik, amelyeken csak három rudat lehet vágni.
Az O2 erő meghatározása. D2. U2 a rácsos rács elemeiben (1.4.1 ábra). Előzetesen megtaláljuk az A és B reakciókat. Az n-n vágást három rúdon végezzük, ahol az erőket határozzuk meg, és a rácsos részek működését a megfelelő O2 vektorok képviselik. D2. U2 feltételezve, hogy az erőfeszítések húzódnak.
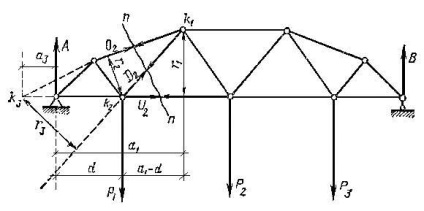
Figyelembe véve a bal oldali egyensúlyt (ahol kevesebb erõ van), három egyenletet alkotunk, amelyek mindegyike csak egy ismeretlent tartalmaz. Ehhez a három klasszikus egyenlet helyett: = 0, = 0, = 0, az egyenlet baloldali részéhez a következő alakot kapjuk:
ahol a pillanatok összege nem tartalmazza az O2 erőfeszítéseit. D2 áthalad a pillanatnyi k1 ponton. A pillanatok összege nem tartalmazza a D2 erőket. U2; az összeg nem tartalmazza az O2, U2 erőfeszítéseit. Minden (1.4.1) egyenlet csak egy ismeretlen erőt tartalmaz, amely megkönnyíti és pontosabban megtalálja. Az U2 meghatározásához. az erõk pillanatainak összegét összegezzük a rácsvonal levágott oldalának levágására, az O2 erõk irányának metszéspontjához viszonyítva. D2:
Itt a számláló nem más, mint a bal külső erők pillanata a ki ponthoz képest (egy szilárd falú képzeletbeli gerenda keresztmetszetének hajlítónyomatéka).
ahol Mvn k1 a bal külső erők pillanata a k1 ponthoz képest;
Most azt találjuk, hogy az O2 erő a farm baloldali szakaszára alkalmazott erő pillanatainak összege, a k2 ponttól, a D2 eltűnő ponttól függően. U2:
A D2 erő meghatározásához válassza ki a k3 pontot - az O2 erők metszéspontjának pontját. U2. A bal oldali egyensúlyt figyelembe véve találjuk
Amint látjuk, a pillanatnyi pontok módszerének alkalmazása során az erőt mindig a külső erők pillanatának arányával fejeztük ki, amely a bal kivágott részre az erő karjára vonatkozik.
Így az U2 erő meghatározása a félig feszítő rács alsó szegmensének elemében (1.4.2. Ábra), egy négyzetes metszésű n-n vágást végzünk.
De a három erő iránya O2. A V2 és V2 1 ugyanabban a pontban metszik egymást. Az U2 meghatározásának pillanatai közé tartoznak:
Hasonlóképpen, az O2 erő meghatározása a k1 ponttal történik.
Zárt vágást alkalmaznak a Shukhov-gazdaság (1.4.3. Ábra) csapágyainak és hasonló rendszereknek a megtalálásához. Tegyük fel, hogy meg kell határoznunk az O1 erőt. a Shukhov tanya felső övének első elemében.
Az O1 oszlopok meghatározott erőknek. O2 és O5 csatlakozik a két fő háromszöghez, elvégezzük azt a vágást, amely egy darabban vágja fel a felső öv rúdjait és a D1 és D2 záróelemeket kétszer.
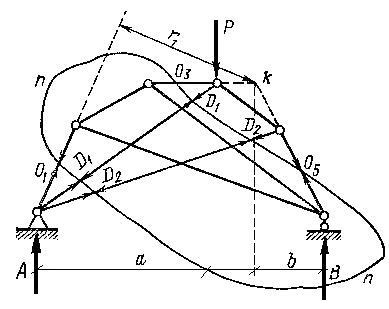
Figyelembe véve a vágás belsejében elhelyezkedő rács egy részét, n-n. az egyensúlyi állapotot úgy alakítjuk ki, hogy a pillanatnyi összegek eltűnnek az O2 és O5 rudak axiális vonalának metszéspontja k-pontjával szemben:
A vetületek módszere akkor alkalmazható, ha a pillanatnyi pont a végtelenségig van, vagyis ha két, egymástól három levágott rúd párhuzamos. Tegyük fel, hogy a D3 farm párhuzamos övekkel való erősségét szeretné meghatározni (1.4.4. Ábra).
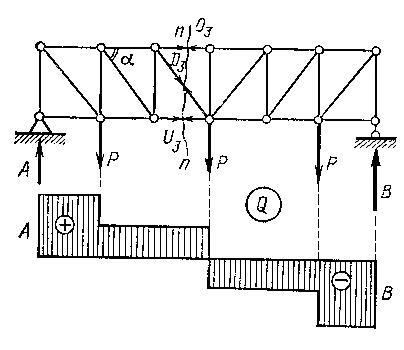
Végezzük el a vágott n-n-t. Három rudat boncolunk, az erőket, amelyekben O3. D3. U3. Az O3 és U3 erőkifejtés iránya. párhuzamosak, ezért a pillanatnyi pont a D3-ra a végtelenségig lesz. A D3 erő meghatározásának problémája könnyen megoldható azáltal, hogy a kivágott résznek az O3 és U3 irányokra merőleges függőleges tengelyre vetített összes erő kiugróinak egyenletét alkalmazza:
ahol (A-P) = Qn a keresztirányú erő az n-n képzeletbeli gerenda egy szilárd falával.
A keresztirányú erő érzékelésén dolgozik egy párhuzamos övvel ellátott rács. A zárójelben lévő erők változásának törvényét a transzverzális erők diagramjából könnyen megállapíthatjuk.
1.4.3 A csomópontok kivágásának módja.
A csomópontok csiszolásának módja a pillanatok módszerével együtt az egyik leggyakoribb módszer az erők meghatározására. A rács minden csomópontján két egyensúlyi állapot alakul ki két vetületi egyenlet formájában két nem párhuzamos tengelyre. Ezért célszerű egy olyan csomóponttal kezdeni, ahol kettő
rúd. Megmutatjuk a csomópontok kivágásának módszerét az erek meghatározására a 3. ábrán bemutatott elemek elemeiben. 1.4.5., A. Az O erő meghatározásához a legegyszerűbb mód a kivágás támogató csomópontjának kivágása (1.4.5.6 ábra).
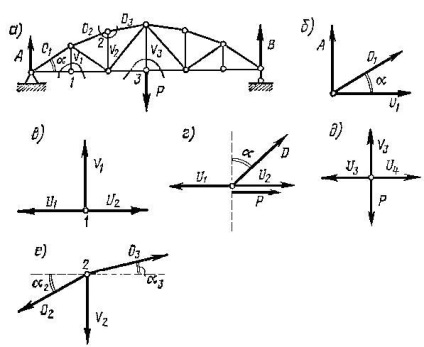
A csomóponton ható erők tervezése, függőleges helyzetben:
azaz a rács felső övének tartóelemében lévő erő arányos a referenciareakcióval.
A V1 és V2 állványok erõinek meghatározásához kivágjuk a rács alsó övének 1 és 3 csomópontjait. és a függőleges tengelyre ráhúzott összes erőt vetjük ki, akkor V1 = 0. Ebből levonhatjuk a következő következtetést: ha három rúd konvergál a csomóponton, ebből kettő ugyanúgy irányul (U1 és U2) és nincs terhelés, az erõ külön irányított rúdban (V1) nulla. Az ilyen rudat zérusnak hívják. Ez a szabály kiterjed azon csomópontokra is, amelyekre a terhelést alkalmazzák, és amely nem rendelkezik olyan komponenssel, amely normális a két másik irányba.
Tegyük fel, hogy egy P vízszintes erőt alkalmaznak azon csomópontra, amelyben a két derék erő U1 és U2 találkozik, és a D záróelemben lévő erőt alkalmazzák (1.4.5. Ábra, d). A csomóponton fellépő erők tervezése, a függőleges oldalon, megtaláljuk: