A helikopter mozgásának mint ellenőrző objektumának modellje
. 10 -5 s -1 - a Föld forgásszögének modulja,
a helikopter látszólagos gyorsulásának vektorát a vízszintes SC-ben;
a gravitációs gyorsulás vektora, amelyet a következő képlet adja meg:
- a vetületi gravitációs erő gyorsító vektora a vízszintes SC [7.5] tengelyén:
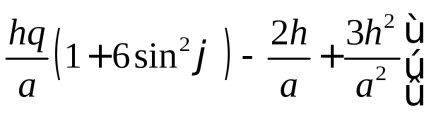
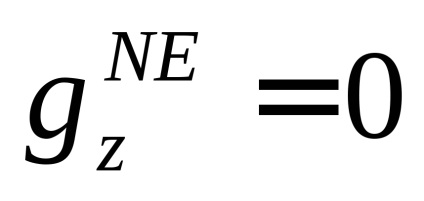
a kifejezés a centrifugális potenciál hatása miatt;
A helikopter térbeli szögmozgását a tömegközépponthoz viszonyítva az alábbi egyenletekkel írjuk le az összekapcsolt SC tengelyének nyúlványaiban:
Ezekben az egyenletekben:
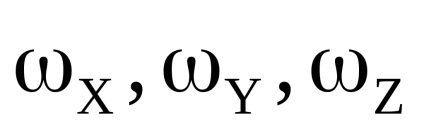

- a teljes pillanatvektor összetevői
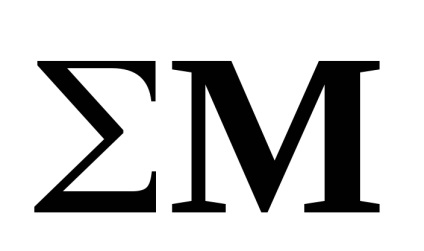
A számításhoz komponens látszólagos gyorsulás, és abszolút szöggyorsulása a helikopter kötött CK használtunk az alábbiakban a rendszer (7,10), linearizált közelében az úgynevezett kiegyensúlyozó röppályáját egyenletek együtthatói függő légsebesség [7,4] kiegészített nemlineáris kifejezéseket az egyenleteket erők lehetővé teszi a nagyobb a szög- és tekercsszögek változásai (az úgynevezett "részlegesen linearizált rendszer"). Az egyenletrendszer írva a hozzá tartozó tengely, és célja, mint már említettük, a tanulmány a repülési feltételeket a sebesség értékek változása 0 és maximum:
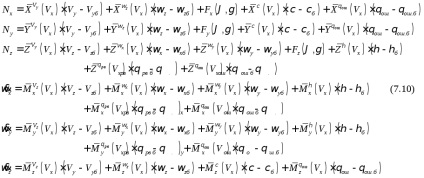
Nx. Ny. Nz - látszólagos gyorsulás vetületei a kapcsolt SC tengelyén;
Vx. Vy. Vz - a helikopter sebessége a kötött SC tengelyén;
Vxb. Vyb. Vzb - a helikopter sebessége a kapcsolódó SC tengelyére a kiegyensúlyozó pályán;
x, y, z - a helikopter abszolút szögsebességének a kapcsolódó SC tengelyére gyakorolt becslései;
xb, yb, zb - a helikopter abszolút szögsebessége a kapcsolódó SC tengelyén a kiegyensúlyozó pályán;
, , - Euler-szögek a helikopter tájolásával (szög, lejtés, tekercs);
o.sh. - a csavar általános lépése;
о.ш.б - a kiegyenlítő pályának a csavar általános lépése;
r.v. - a kormánycsavar menetét (egy kormányzárral ellátott séma esetén);
r.v. - a kormánycsavar (egy kormányzárral ellátott séma esetében) kiegyensúlyozó pályán való pályán;
a szalaglemez hosszanti eltérésének szöge;
b - a szalaglemez hosszanti eltérésének szöge a kiegyensúlyozó pályán;
a szalaglemez keresztirányú eltérésének szöge;
b a szalaglemez keresztirányú eltérésének szöge a kiegyensúlyozó pályához;
- az aerodinamikai erő kivetítésének származékai az összekapcsolt SC X tengelyén a mozgás és a vezérlés paraméterein;
- az aerodinamikai erő Y tengelyére történő mozgatásának származékai a mozgásvezérlés paraméterei alapján;
- az aerodinamikai erőnek a kapcsolt SC Z-tengelyére történő vetületének származékai a mozgás és a vezérlés paraméterein;
- az aerodinamikai nyomatéknak az összekapcsolt SC X tengelyére történő kivetítésének származékai a mozgás és a vezérlés paraméterein;
- az aerodinamikai nyomatéknak az összekapcsolt SC Y tengelyére való vetülete származékai a mozgás és a vezérlés paraméterein;
- az aerodinamikai nyomatéknak az összekapcsolt SC Z tengelyére történő vetületének származékai a mozgás és a vezérlés paraméterein;
Az egyenleteket (7.10) úgy kapjuk meg, hogy kiterjesztjük a helikopterre ható erőkre és pillanatokra vonatkozó Taylor-sorozatokat a kiegyenlítő pályák közelében. Itt, a kiegyenlítéssel azt értjük, hogy a traktóriák halmaza a statika egyenletrendszerének megoldása eredményeképpen jött létre. nulla aerodinamikai pillanatoknál és nulla csúszási szögnél [7.4].
Az egyenletek (7.10) alkalmazása során fellépő dinamikus hibák csökkentése, azaz hibák jelenléte által okozott térhálósítás, a nemlineáris kifejezések Fx (, ), Fy (, ), Fz (, ) bevezette korrigáltuk a befolyása ryskanya szög [7.3]. Hogy megszüntesse dinamikus hibák által okozott tranziensek ha változik a módok kiegyensúlyozó, interpolációs táblázat adatok leképezését egy spline interpoláció, amely megközelíti az eredeti táblázatban B-spline rendszer [7.6] a követelménynek a kielégítésére a folytonossági megoldások C 1.
A következő közelítési technikát alkalmaztuk. A B-spline alapon megépített görbét a következőképpen írjuk le [7.6]:
ahol
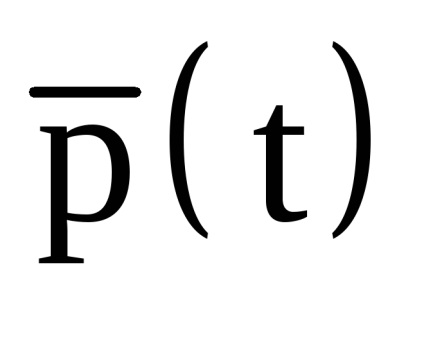

Nik (t) az i-edik normalizált B-spline súlyfüggvénye a k k-k-ből (vagyis a k-1-es fokozatból álló) bázis görbéből, amelyet visszatérési összefüggések adnak meg:
Itt xi a csomóvektor elemei, t pedig a paraméter, amely 0-tól tmax = (n-k + 2) -ig változik.
Egy csomóvektor, amelynek hossza (n + k + 1) be van vezetve a B-spline görbék belső görbületének kiszámításához, és az egész számok-paraméteres csomópontok nondecreasing szekvenciája. A csomóvektor a hozzávetőleges vonallánc pontjai számával, a görbe sorrendjével és összetett (többszörös) csomópontok jelenlétével határozható meg.
Ismert [7.6], hogy a B-spline görbe a polinom foka (k-1) minden intervallum (xi, xi + 1), és az összes származékai a (k-2) edrendű folytonosak teljes íve mentén, ez a görbe a k sorrendű függvénye.
Így a B-spline rendszernek a táblázatos adatok közelítésénél lehetővé kell tenni egy folyamatos kiegyenlítést egy egyensúlyi üzemmódból a másikba, és gyakorlatilag megszünteti az eredményül kapott dinamikus hibákat.
Az egyenletek jobb oldalán (7.10.) Szereplő perturbációk összetételében szükség van egy további aerodinamikai terhelésre, amely a szél hatásából származik, és a helikopter mozgásának leírásában a fő nem ellenőrzött tényező. A szél által előidézett perturbáció a helikopter légsebességének vektorában bekövetkezett változást eredményezett, és ennek következtében a támadás és csúszás szögének változása. Ez viszont az aerodinamikai erõk és pillanatok megfelelõ változásaihoz vezet, amelyek szükségesek a látszólagos gyorsulás összetevõinek és a helikopter abszolút szögsebességének a hozzá tartozó SC-ben való kiszámításához. A modell nem veszi figyelembe a propeller csapágypengék hajlításával és az aerodinamikai hatékonyságuk megváltozásával járó hatásokat, valamint a további jelenség összetettségének köszönhető további örvényáramok kialakulását, ami további vizsgálatot igényel.
Általános esetben, figyelembe véve a szél hatását, a légsebesség-vektort a következőképpen kell írni:
VB - légsebességű véletlen mozgás (helikopter esetében egybeesik a sebességvektorral egy földrajzi SC-ben);
WB - szélsebesség vektora.
Ennek a modellnek a keretében a szél meghatározó determinisztikus vízszintes rohanásnak számít. feltételezzük, hogy nincsenek légi tömegek függőleges elmozdulása; a sebesség abszolút értéke függ a pont magasságától és földrajzi koordinátáitól, és az irányt az azimut szög jellemzi, azaz az azimut szög. a szél irányát az északi irányhoz viszonyítva.
A helikopter alacsony magasságú repülésének vizsgálatakor két megközelítést alkalmaznak a lapos szél kívánt jellemzőinek kialakításához:
Állandó szél, amelynél a sebességmodul kifejezetten be van állítva (
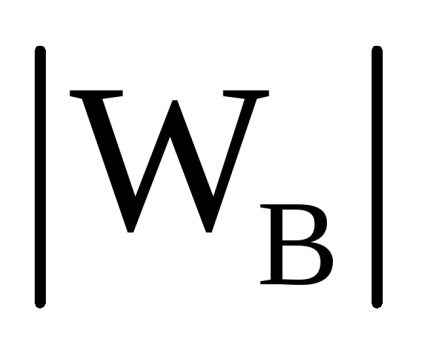
Szél a profil mentén, amikor a szélsebesség abszolút értékét és az azimut szögét a szélsebesség profilja közötti közelítéssel határozzuk meg (a 7.7-7.8. Ábrák).
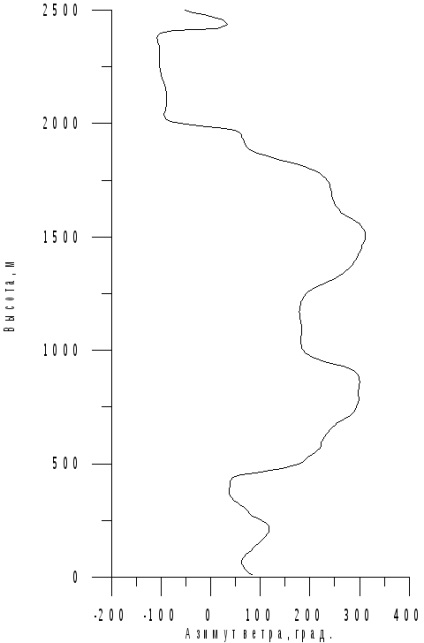
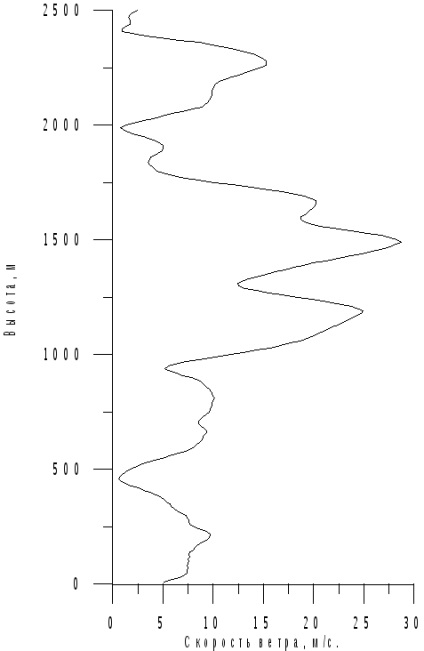
Ezután a földrajzi SC-ben az eredményül kapott szélsebesség-vektort a kapcsolódó SC-re vetítjük, ahol a helikopter sebességének teljes vektorával összegezve a légsebesség-vektort (7.12) képezzük.
Mivel az arány kiszámításához a látszólagos gyorsulás komponenst és az abszolút szöggyorsulása a helikopter rögzített kötött CK, a számviteli zavarok által okozott szél, végezzük megváltoztatásával aerodinamikai erők együtthatók segítségével, mivel a légsebesség modul érv kapcsolódó SC:
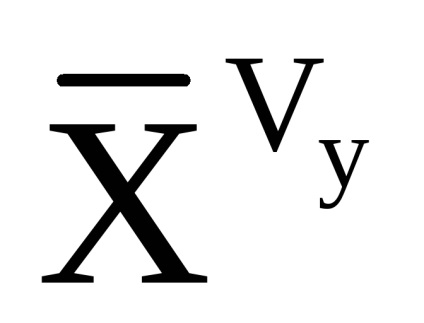
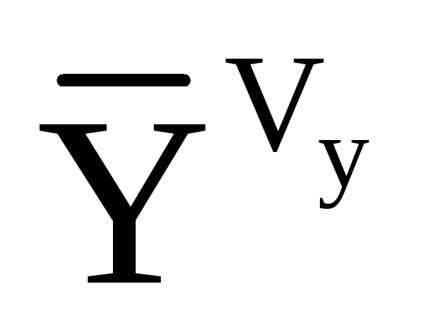
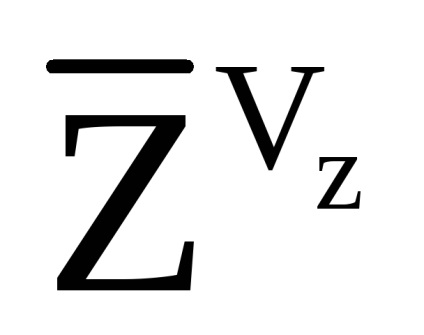
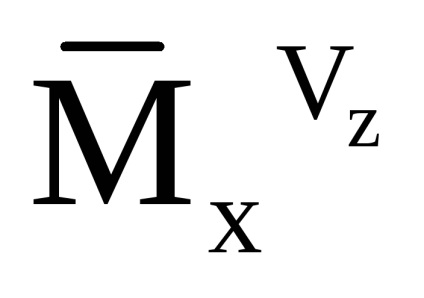
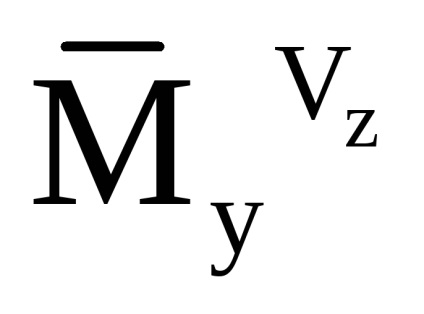
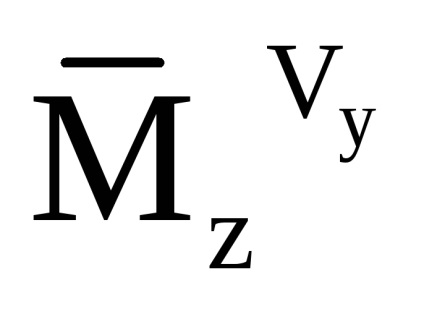
A látszólagos gyorsulás újraszámítása a vízszintes SC-ben a következő összefüggést alkalmazza:
- a helikopter látszólagos gyorsulásának vektorát az összekapcsolt SC-ben a (7.10) alapján kiszámítva.
Az átmeneti mátrixot a vízszintes SC-ről a kapcsolt állapotra a Rodrig-Hamilton paraméterek [7.2] alapján határoztuk meg. Ez a megközelítés egy merev test véges forgatásának ábrázolásán alapul, a saját koordinátarendszer transzformációjának kvaternójában, amelynek összetevői Rodrig-Hamilton paraméterek.
A klasszikus kinematikus egyenletekkel összehasonlítva a kvaternionok használata lehetővé teszi egy nagy pontosságú, stabil, numerikus megoldást, amely egyetlen ponttól mentes, és biztosítja a tengelyek kölcsönös ortogonalitását a koordináták újraalkalmazásában:
ahol q1. q2. q3. q4,

A kinematikus egyenleteket ebben az esetben vektoros formában írják [7.2]:
ahol "

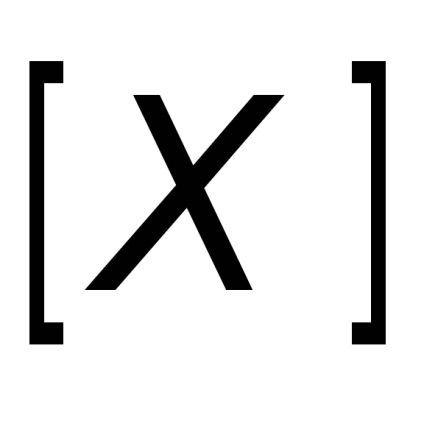
A hagyományos Euler szögek (, , ) az átmeneti mátrix alapján határozhatók meg
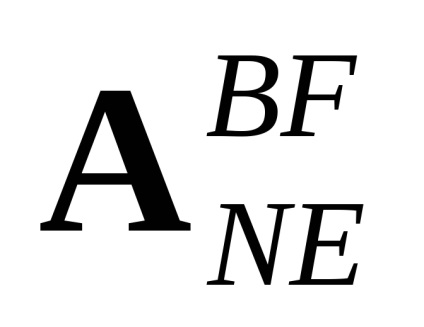
ahol aij a mátrix komponense
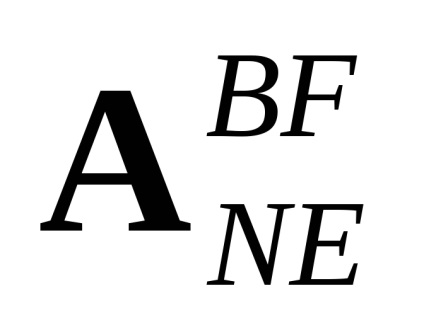
Ily módon egy teljes rendszer differenciálegyenletek részlegesen linearizált közelében a kiegyenlítő útját, és leírja a térbeli mozgását a helikopter, tartalmaz egy 6 cm mozgást egyenletek (7,7), és az azt kiszámító egyenlet a vektor komponenseit a látszólagos gyorsulás és szöggyorsulása a helikopter alkotó rendszert (7,10), korrelációs egyenletek látszólagos gyorsulás a földrajzi SC (7,11) és a négy kinematikus egyenletet (7,15), amely leírja a változás dinamikája Rodrigues-Hamilton paramétereket.