Szokatlan aritmetika 1954
Rendkívüli aritmetika
A számtani műveletekhez hozzászoktunk, hogy automatikusan elvégezzük őket, szinte anélkül, hogy elgondolnánk, mit csinálunk. De ugyanezek a lépések sok erőfeszítést igényelnek tőlünk, ha alkalmazni szeretnénk azokat a számokra, amelyeket nem a tizedes rendszerben írtunk. Próbálkozzon például a következő két szám megadásával a centenáriumi rendszeren:
Hajtsa be a számjegyeket, kezdve az egységekkel, vagyis a jobb oldalon: 3 + 2 5; de nem írhatunk 5-et, mert nincs ilyen szám a centenáriumi rendszerben: az 5 már a legmagasabb rend egység. Ezért az összegben egyáltalán nincsenek egységek; 0 és 5, vagyis a következő számjegy egységét jegyezzük meg. Továbbá 0 + 3 = 3, és még az egység is megtartja az elmét, csak 4 egység a második szint. A harmadik számjegyben 2 + 1 = 3 lesz. A negyedik 4 + 2-ben 6, azaz 5 + 1; 1-t és 5-t írunk, vagyis a legmagasabb kategória egységét, a továbbiakban balra hivatkozunk.
A szükséges összeg 11340.
Ezt a kiegészítést az olvasónak hagyjuk, ha először a számokat idézőjelekkel tizedes rendszerbe fordítjuk.
Ugyanígy más műveleteket is végrehajtunk. Az edzéshez számos példát adunk meg, amelyek száma az olvasó, ha kívánja, önállóan növekszik:
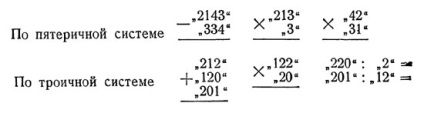
A centenáriumi rendszeren: "1304", "1144", "2402".
Az ilyen műveletek végrehajtásakor először mentálisan képviseljük az írott számokat a szokásos decimális rendszerben, és miután megkaptuk az eredményt, ismét képviseljük a szükséges nem decimális rendszerben. De ugyanezt teheti: hozzon létre egy "hozzáadási táblát" és egy "szorzótáblát" ugyanabban a rendszerben, amelyben számokat adunk nekünk és közvetlenül használjuk őket. Például a pentenáriumi rendszerben található hozzáadás táblázat a következő:
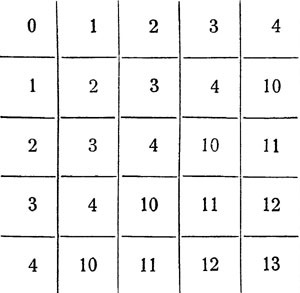
Ezzel a tabletta segítségével a "centrális" rendszerben a "4203" és a "2132" számokat felvehetjük, sokkal kevésbé hangsúlyozva, mint korábban alkalmazott módszerrel.
A kivonás szintén egyszerűsödik.
A centenáriumi rendszernek a szorzótáblát is ("Pythagorov" *) alkotjuk:
* (Pythagoras (ie 6. század) egy ősi görög filozófus, matematika és zeneelméletet is tanulmányozott.)
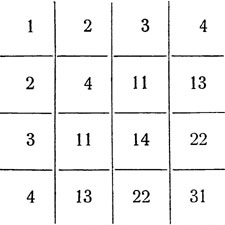
Miután ezt a lemezt a szeme elé helyezte, ismét megkönnyítheti számodra, hogy többszöri (és oszd meg) a számokat a februári rendszerben, ahogyan a fenti példákon keresztül is könnyen láthatod. Például, amikor megszorozza
úgy gondoljuk: háromszor három "14" (az asztaltól); 4 írj, 1 - az elmében. 1 a 3-ban megadja a 3-ot, és még az 1-t is, - írja 4. Háromszor három = "11"; 1 írj, 1 balra. Az "1144" eredményt kapjuk.
Minél kisebb a rendszer alapja, a kisebb és a hozzá tartozó kiegészítések és szorzások táblái. Például egy terner rendszer esetén mindkét táblázat a következő:
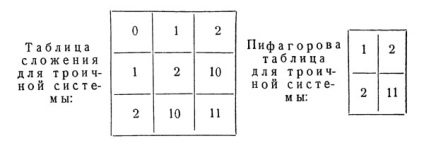
Rögtön emlékeztek rá és használhatják a cselekvést. A legkisebb hozzáadási és kivonási táblázatokat a bináris rendszerhez kapjuk:
Ilyen egyszerű "táblázatok" segítségével mind a négy műveletet elvégezheti a bináris rendszerben. A rendszer ebben a rendszerben való szaporodása lényegében nem, egyáltalán nem: végül is, az egyik eszközzel a szám változatlanul hagyása; A szorzással "10", "100", "1000" (azaz 2, 4, 8) szorozva egyszerűen hozzárendeli a megfelelő nullát a jobb oldalon. Ami a kiegészítést illeti, annak megvalósításához csak emlékeznie kell arra, hogy a bináris rendszerben 1 + 1 == 10. Nem igaz, hogy joggal neveztük a bináris rendszert a lehető legegyszerűbbnek? Ennek a különös számtani számnak a hossza az egyszerűség, hogy minden aritmetikai műveletet elvégezzen fölöttük. Szükséges például, hogy szaporodjon:
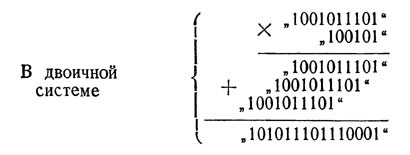
Egy cselekvés végrehajtása csak a hosszú számok újraszövegezésére korlátozódik a megfelelő elrendezésben: ehhez páratlanul kevesebb mentális erőfeszítésre van szükség, mint ugyanazok a számok szorzata a tizedes rendszerben (605 X X37 = 22385).
Ha elfogadnánk egy bináris rendszert, akkor az írásos jelölés tanulmányozása a legkisebb gondolatmenetet igényli (de a legnagyobb mennyiségű papír és tinta). Azonban egy szóbeli beszámolóban a bináris számtani az akciók elvégzésének kényelméért jóval alacsonyabb a decimális számnál.
A bináris rendszerben végrehajtott divízió mûködésének mintáját is bemutatjuk:
A szokásos decimális rendszerben ez a következő lenne:
Az osztalék, az osztó, a hányados és a maradék lényegében ugyanaz mindkét esetben, de a közbenső számítások eltérőek.