A sík szögek vetületére, leíró geometriára
1. Ha a sík, amelynél némi szög van, merőleges a vetületek síkjára, akkor ez a vetületre vetül ki egyenes vonal formájában.
2. Ha a derékszög síkja nem merőleges a nyúlványok síkjára, és legalább egyik oldala párhuzamos ezzel a síkkal, akkor a derékszög egyenes szög alakú.
Tegyük fel, hogy az ACB jobb szög CB oldalán (89. ábra) párhuzamos a vetületek síkjával. Ebben az esetben a CB vonal párhuzamos a C ° B ° -val. Tegyük fel, hogy a derékszög második oldala (A) a K ponton metszi az A ° C ° csúcsát. A K ponton átívelő síkban a C ° B ° -val párhuzamos vonalat rajzolunk. A KL egyenes vonala párhuzamos a CB-vel, és a CKL szöget egyenesen kapja meg. A három függõleges tétel elmélete szerint a C ° KL szög egy sor 1). Következésképpen az A ° C ° B ° szög is egy sor.
1) Egyenes vonalakhoz tartozó pontok, amelyek azonos vetítővonalon helyezkednek el, a "versenyző" név fordul elő.
A derékszögű vetületre vonatkozó tétel két inverznak felel meg (§§ 3 és 4).
3. Ha a sík szög vetülete derékszöge, akkor a vetített szög csak akkor lesz egyszerű, ha ennek a szögnek az egyik oldala párhuzamos a vetületek síkjával.
4. Ha egy bizonyos szögű vetület, amelynek egyik oldala párhuzamos a vetület síkjával, egy derékszög, akkor a vetített szög egyenes.
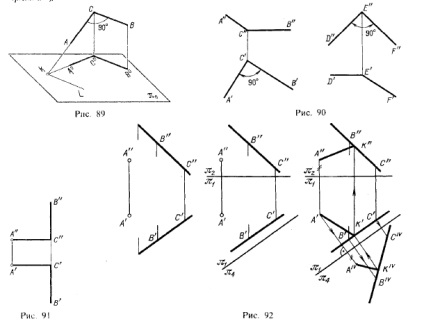
A fentiek alapján megállapítható, hogy a 2. ábrán látható szögek 90, egyenesek a térben.
Abban az esetben, ha két nyílási sík derékszöge van egyenes szögben? Ez akkor történik, ha a derékszög egyik oldala merőleges a harmadik kiálló síkra (a másik oldal pedig a síkkal párhuzamos). 91: az AC oldal merőleges a π3-ra. a nap oldalán párhuzamosan π3.
A dőlésszöggel kapcsolatos információk felhasználásával a π1 rendszer hozzáadásával. π2 a π4 rendszerrel. π1 (§ 8), és a helyét a nyúlványok egy párhuzamos egyenes egy projekciós síkon (§ 11), tudjuk elvégezni az alábbi konstrukciót: navigálni egy pont egyenes vonalat úgy, hogy áthaladt a sorban alatt-90 ° -os könyök, az oldatot ábrán látható , 92, de a bal kezdőpontot kapja, középen a képződés látható, kivéve az 1. rendszert. Π2. egy másik π4 rendszer. π1. és pl. kπ4 || BC, és az egyenes AK⊥BC konstrukciója jobbra történik.
1) A három függőleges direkt tétel szerint: ha KL⊥ K, akkor KL.⊥SK. Az átértelmezett tétel szerint: ha KL⊥SK, akkor KL⊥єK.
2) Az inverz tételek bizonyítása érdekli a könyv korábbi kiadásait,
Mivel pl. π3 || Sun, amely el van látva, hogy a gazdaság tengelyre pi; 4 / π1 párhuzamos B'C”, közvetlen ygol AKV (vagy kivetített AKCj MP pi ;. 4, mint a közvetlen azonos szögben A IV K IV B IV megépítésének vetülete az A pont és az egyenes vonal BC a tér pi; .. tartsa 4 a IV K IV ⊥B IV C IV és Tatem kapjunk vetítési K 'és K', valamint a nyúlvány A'k „és egy "R"(az építési nyilakkal jelzett) ..
Lehet-e feltételezni? Miután meghatároztuk a merőleges AK-t a BC egyenesen, meghatároztuk-e az A-tól a BC-ig terjedő távolságot? Nem, csak építettük az AK szegmens előrejelzéseit; egyikük sem határozza meg a távolságot. Ha meg kell határozni az AK szegmens értékét, vagyis az A-tól a BC-ig terjedő távolságot, akkor folytatni kell a konstrukciót, legalább a 13. §-ban leírt módszert alkalmazva.
5. Ha a sík tompaszöget vagy akut szög nem merőleges a síkra projekció, és legalább az egyik oldalon síkjával párhuzamosan a vetítési szög, a vetítési tompaszög erre a síkra van tompaszögben, és hegyesszöget vetítési - hegyesszögben.
Tegyük fel, hogy a CB vonal (93. ábra) párhuzamos a vetületek síkjával. Vegyük figyelembe az SWR tompaszögét vagy az MSW akut szöget, és vonjunk egy vonalat CL⊥CB-t e szög síkjába. Mivel az LCB szög egy egyenes, a vetülete az LC ° B ° szög
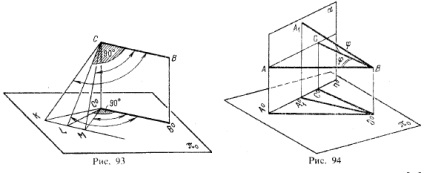
szintén derékszögű. Ez a szög a CC ° B ° szög alatt helyezkedik el, és belülről bezárja az MC ° B ° szöget, így a KC ° B ° szögű, és a M ° ° B ° szög akut. Így a szög vetülete olyan szög, amelynek ugyanaz a neve (egyenes, tompa vagy éles), mint maga a szög, ha a szög legalább egyik oldala párhuzamos a vetületek síkjával. Általánosságban bármely szög vetülete lehet egy akut, egyenes vagy tompaszög, attól függően, hogy a szög milyen helyzetben van a vetület síkjához viszonyítva.
6. Ha bármelyik szög mindkét oldal párhuzamos a vetületek síkjával, akkor annak vetülete egyenlő nagyságú a vetített szöggel.
Ez a párhuzamos és azonos módon irányított szögek egyenlőségéből következik.
Ezért például az AB vonal (50. ábra, 27. o.) És pl. π2 könnyen meghatározható: az ego az A'B és az x tengely közötti szög; ugyanúgy, mint a CD és a négyzet közötti szög. π1 (51. ábra) a C "D" és az x tengely közötti szög, az EF (52. ábra) és a négyzet közötti szög. π2 - az E "'F"' és a z tengely között.
Dőlésszög esetén a vetület és a szög közötti egyenlőség akkor is megegyezik, ha a derékszögnek csak az egyik oldala párhuzamos a vetületek síkjával.
De egy olyan akut vagy tompaszög esetén, amelyben az egyik oldal párhuzamos a vetületek síkjával, a szög kivetítése nem lehet egyenlő a vetített szöggel. Ebben az esetben az akut szög vetülete kisebb, mint a vetített szög, és a vetemedés vetülete nagyobb, mint a vetített szög.
Hagyjuk (94. ábra), hogy az A1 BC szög legyen akut és a CB oldalán a négyzet párhuzamos. π0; C ° B ° || ST. Pl. a CB-re merőleges C ponton keresztül merőleges a négyzet. π0. metszve az utat a n ° vonal mentén, áthaladva C ° -on és merőleges a C ° B ° -ra. Ha a B ponton keresztül rajzolunk különböző egyenes vonalakat ugyanolyan hegyes szögben, mint a CB egyenes, akkor ezek mindegyike metszi pl. Azon pontokban, amelyeknek az előrejelzései a sorban állnak. Tegyük fel, hogy az AB és az A1 B vonalak a CB vonallal egyenlő szögeket alkotnak: ∠ ABC = ∠A1 BC. Ha ebben az esetben az AB párhuzamos a π0 síkkal. majd ∠ A ° B ° C ° - ∠ ABC. Ha az A1B oldal nem párhuzamos a π0-vel. akkor az A1 pont kinézete a C pontnál közelebb eső vonalban van, mint az A pont kivetítése. Következésképpen az A1 BC szög vetülete az A ° B ° C ° szögnél kisebb, azaz A ° B ° C ° 1).
9. Ha a szög oldalai egyenlően hajlanak a vetületek síkjához, akkor a szög-vetület nem lehet egyenlő a vetített szög
Ez (95. ábra) úgy hozható létre, hogy összekapcsolja az MKN szöget és az π.π0 szöget, miközben forgatja az MN vonal körül. Ebben az esetben az MK ° N szög az MK1 N szög alatt van, és a csúcsok K1 és K ° a közös merőleges MN-re.
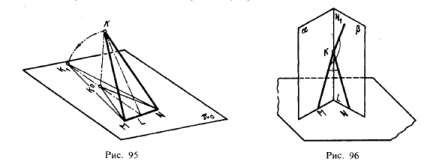
9. Az éles és tompított szögek nyúlványai nem lehetnek egyenlők a vetített szöggel, ha a vetületi sík oldalai párhuzamosak.
Az 1. ábrából. 96 láthatjuk, hogy minden szög, például az MKN akut szöge és az MKN1 tompaszög. amelyek oldalai a kiálló síkokban helyezkednek el. és. a vetítési szöggel megegyeznek az MLN szögével, és ezek a szögek megközelíthetik a 0 ° -ot és a 180 ° -ot. Nyilvánvaló, hogy ezen szögek között van egy olyan szög, amely megegyezik a vetületével.
Ilyen szögbeli példa a 38. §-ban található.
KÉRDÉSEK 13-15
- Hogyan készítsünk négyszögletes háromszöget a rajzon, hogy meghatározzuk az egyenes vonal hosszát általános helyzetben és annak szögét a π1 és π2 nyúlványok síkjaival?
- Milyen feltételek vannak az általános pozíció vonala és az π1 és π2 vetületek síkjai között?
- Mi a párhuzamos egyenes vonalak párhuzamos vetületi tulajdonsága?
- Lehet-e meghatározni, hogy a két profilvonalak a π1, π2 rendszerben rajzolódnak-e, hogy ezek a vonalak párhuzamosak-e egymással?
- Hogyan ábrázolják a két, egymással metsző egyenes vonalat a π1, π2 rendszerben?
- Hogyan értelmezhetjük két átkelő vonal metszéspontját?
- Melyik esetben a derékszöggel sugárzott derékszög van?
- Melyik esetben a tompa vagy éles szög vetülete szükségszerűen ugyanolyan névvel (tompa vagy akut)?
- Lehetséges-e az akut vagy elmosódott szög kivetítése, amelyben az egyik oldal párhuzamos a vetületek síkjával, egyenlő a nagyon szögben az űrben?
- Melyik esetben a szög metszésének felosztása megegyezik a szög ilyen szétválasztásával az űrben?
- Lehet-e a szög-vetület egy bizonyos vetületi síkban megegyezik a vetített szöggel, amelynek oldalai egyenlőek ezzel a síkkal?
- Lehet-e olyan akut vagy tompaszög, amelynek az oldalai nem párhuzamosak a vetületek síkjával, egyenlő a vetületük ezen a síkon?