A grafikon absztraktja a juhar rendszerben v - absztraktok, esszék, beszámolók, kurzusok és oklevelek
ZD típusú csöveket épít.
Ezek közül a funkciók közül először is meg kell jegyezni, hogy számos új típust ábrázol (pl. Azonos szintű vonalak, vektor mezők stb.), Valamint a különböző grafikonok egyesítésének módjait. Különösen érdekesek az első két funkció, amely animációt (animációt) nyújt kétdimenziós grafikonként (animált) és háromdimenziós (animate3d). Ez a csomag elég
megérdemli, hogy külön könyvben lehessen leírni. De a könyv korlátozott volumenét figyelembe véve, csak néhány jellemző példát tekintünk az alkalmazásnak. Vegye figyelembe, hogy ezeknek a funkcióknak a használatához szükség van egy csomaghívásra, például a (with) paranccsal.
13.6.2. A funkciók grafikonjainak szerkesztése egy kétdimenziós poláris koordináta-rendszerben
A plot-csomagban van egy függvény a grafikonok ábrázolásához a poláris koordinátarendszerben. Láncolat alakú (L, o), ahol L olyan objektum meghatározására szolgáló objektum, amelynek grafikonja ábrázolva, és o opcionális opciók. Az 1. ábrán. A 13.27. Ábra a polarplot függvény ábrázolásának példáját mutatja.
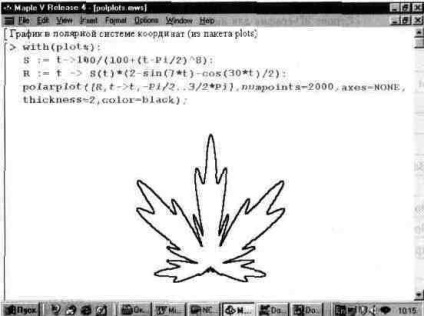
Ábra. 13.27. A polarplot függvény segítségével létrehozott gráf.
Ebben az esetben a nagyobb expresszivitás érdekében a koordinátatengelyek kiépítését el kell hagyni, és a grafikont kétszeres vastagsággal vonjuk le. A grafikon nagyon hasonlít a juharfalevélhez, nagyon tisztelt Kanadában, és a Maple V rendszer emblémájává vált.
13.6.3. Plotting vonalak azonos szinten
Az egyenlő vonalú vonalakkal (kontúrgrafikonokkal is) felépített grafikonokat gyakran használják a térképészetben. Ezeket a grafikonokat akkor kapjuk meg, ha mentálisan rajzolunk egy háromdimenziós felületen egy sor egymástól egyenlő síkot, amelyek párhuzamosak a grafikon X és Y tengelyével kialakított síkkal. Az egyenlő magasságú vonalak a síkok háromdimenziós felületű metszéséből származnak.
Az ilyen grafikonok létrehozásához a kontúrplot funkciót használjuk, amely több formátumban használható:
kontúrvonal ([exprf, exprg, exprh], s = a..b, t = c..d)
kontúrvonal ([f, g, h], a..b, c..d)
kontúrvonal3d ([exprf, exprg, exprh], s = a..b, t = c..d) ""
kontúrplot3d ([f, g, h], a..b, c..d)
Itt - f, g és h - funkciók, expri - egy kifejezés, amely leírja a függőség a magassága a felület a x és y koordináták, exprf, exprg és exprh - expresszió, attól függően, hogy s és t, és írja le a felület paraméteres formában, hanem a B - állandó anyag, típus, végállandók vagy valós típusú kifejezések, x, y ,, s és t a független változók neve.
Az 1. ábrán. A 13.28 ábrán egy gráf ábrázolása egyenlő szintű vonalakra vonatkozik egyetlen funkcióra. A feltöltött = true opció automatizált színezést biztosít az egyenlő szintű vonalakból álló zárt formák számára. Néha ez a grafika sokkal kifejezőbb, mint amikor csak egyenlő szintű vonalakat épít.
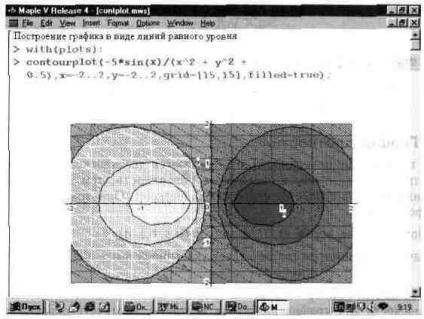
Ábra. 13.28. Példa az egyenlõ szintû vonalakra vonatkozó függvénygrafikon ábrázolására.
A függvény kontúrolaj lehetővé teszi számos függvény létrehozását és grafikonját. Az ilyen konstrukció egy példáját az 1. ábrán mutatjuk be. 13.29. Az ábrán szereplő köröket a c1, c2, c3 és c4 függvények által definiált négy felület alkotja.
Meg kell jegyezni, hogy bár a grafika formájában azonos szintű sorok ne nézd esztétikus és természetes, mint a szokásos grafikai háromdimenziós felületek (az igénylő az eredmények értelmezése), egyetlen fontos előnye - a szélsőséges funkciók a következő grafikonok kiderül néha világosabban hagyományos térképek. Például egy kis emelkedés vagy depresszió a nagy "hegy" egy rendes diagram lehet láthatatlan, mivel homályos
"Hegy" - az egyenrangú vonalak diagramján ez a hatás nincs jelen. Az ilyen grafikonok kifejező ereje azonban erősen függ az azonos szintű vonalak számától.
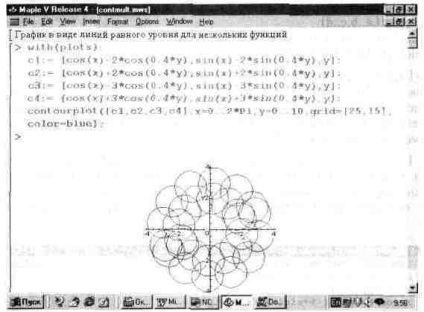
Ábra. 13.29. Példa a sok funkció grafikonjainak egyenlő szintű vonalakra történő ábrázolásával.
13.6.4. A sűrűség grafikonja
Néha háromdimenziós felületek jelennek meg a síkban a színsűrűség grafikájaként - annál magasabb a felületi magasság, annál sűrűbb a szín. Ezeket a grafikonokat a densityplot funkció hozza létre. Két formátumban rögzíthető:
ahol a paraméterek hozzárendelése megegyezik a kontúr-plot funkcióval fent megadottal.
Az 1. ábrán. 13.30 példa erre a diagramra. Nem nehéz látni, hogy az X, Y síkban a gráf négyzetekre oszlik, amelyek színe sűrűsége eltérő. A mi esetünkben a színsűrűség szürke árnyalatú.
Általában az ilyen típusú grafikák nem túl kifejező jellegűek, de saját alkalmazási területeik vannak. Például egy áttetsző folyadék színének árnyalata jelezheti a tartály fenekének felületét, amelyben a folyadék található.
13.6.5. Kétdimenziós vektor térképe
A háromdimenziós felületek megjelenítésének másik gyakori módja a vektor térképe. Gyakran használják mezők megjelenítésére, például elektromos töltésekre. A különlegessége az ilyen grafika, hogy felhasználjuk az őket nyíl, amelynek iránya megfelel az irányváltások során a gradiens mező és a hossza - az érték a lejtőt.
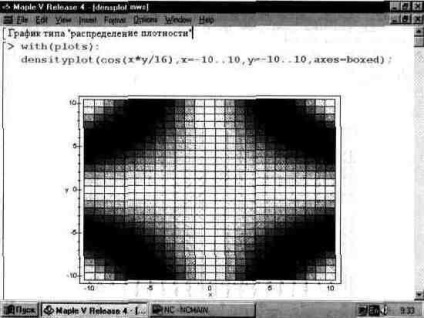
Ábra. 13.30. Egy adott függvény sűrűségi görbéje.
Az ilyen grafikonok kétdimenziós koordináta-rendszerben történő létrehozásához használja a fieldplot függvényt:
fieldplot (f, rl, r2) vagy fieldplot (f, rl, r2),
ahol f az vektor vagy a vektorok halmaza, amelyek meghatározzák az építést, és rl és r2 határértékek.
Az 1. ábrán. A 13.31 egy ilyen grafikon egyik nézete. Meg kell jegyezni, hogy ahhoz, hogy elegendő számú jól látható nyilat érhessünk el, meg kell dolgozni a grafikonok formázásával. Ellenkező esetben az ilyen grafikonok nem feltétlenül reprezentatívak. Tehát a túl rövid nyilak kötőjellé alakulnak, és még olyan pontokra is, amelyeknek nincs pontjuk, ami megfosztja az egyértelműség grafikáját.
Egy kicsit később figyelembe vesszük a sűrűség és vektor mezők építését egy rajzban, valamint a láthatóbb zsír nyilak létrehozását.
13.6.6. Grafikonok különböző koordináta-rendszerekben
A plot-csomagban számos funkció van a diagramok ábrázolásához különböző koordináta-rendszerekben. A kötet mennyisége nem teszi lehetővé az ilyen grafikonok reprodukciós példáit, mert sok száz. Igen, ez nem szükséges - a súgórendszerbe beágyazott példákban megtalálhatja az összes szükséges információt. Tehát a funkcionális csövek (C, opciók) alkalmazásának néhány példájára korlátozódunk, amely lehetővé teszi számodra, hogy nagyon intuitív alakokat építsenek ki a térben, hasonlítanak a csövekhez vagy más tárgyakhoz, amelyek rotációs számokból állnak.
Az 1. ábrán. 13.32 a számok egyike látható. Ez feltűnően hasonlít a csiga héjához. A funkcionális színezést úgy érik el, hogy finomítják a diagramot a formátumsáv használatával. A C paraméter jelentése (a Conchoid dokumentumban) könnyen érthető ebből a példából.
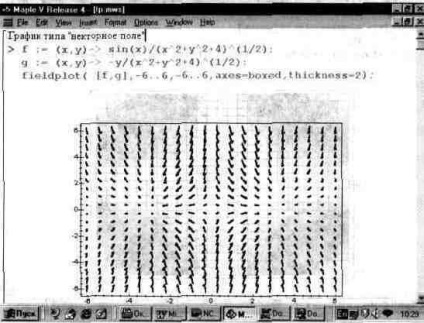
Ábra. 13.31. Kétdimenziós grafikon a vektor mező típusáról.
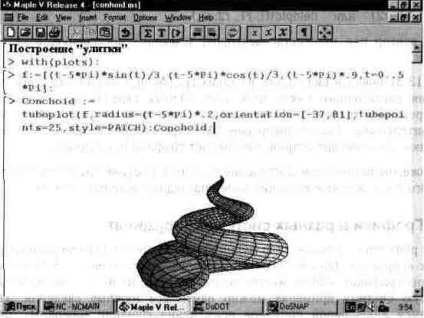
Ábra. 13.32. A "csiga" ütemtervének ábrázolása.
Ez a funkció arra is alkalmas, hogy több csöves tárgyat alakítsanak ki a térben. Ez automatikusan beállítja az algoritmust a láthatatlan vonalak eltávolítására, még meglehetősen bonyolult formák esetén is. Ezt példázza
ábrán. 13.33, bemutatva a "lánc" ábráját. Nem csodálatos ez a szám reálisja?
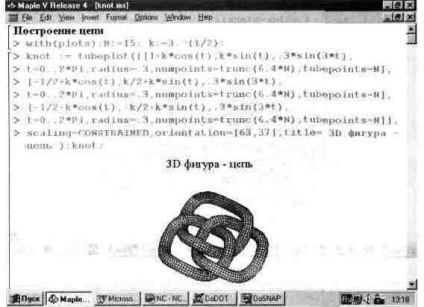
Ábra. 13.33. Ábra "lánc", amelyet a "tubeplot" funkcióval építettek fel.
Lehet sokat gondolkodni arról, hogy a természet a „tanult” a matematikai törvényszerűségek alapját képező egyes geometriai objektumok, vagy talán a zseniális az emberek, akik képesek voltak megtalálni az ilyen törvények természeti tárgyak. A mai Maple V nagy lehetőségeket kínál az ilyen emberek számára.
13.6.7. Háromdimenziós vektortípusok grafikonjai
Számos grafikon láthatósága lényegesen megnövelhető úgy, hogy háromdimenziós ábrázolásba épít. Például a vektor mezők építéséhez használhatja a grafikus funkciót: fieldplot3d. A funkció területplotjától eltérően a nyilakat úgy alakítja ki, mintha háromdimenziós térben lenne (13.34. Ábra).
Az ilyen kétdimenziós grafikonok szingularitásairól mindössze annyit említenek, hogy a háromdimenziós grafikonok érvényesek. Különösen a megfelelő reprezentativitás elérése érdekében gondosan debugolni kell az ilyen grafikonok megjelenítési formáit.
13.6.8. Contour 3D grafika
A vektorgrafikus grafikákkal ellentétben a háromdimenziós felületek kontúrgrafikája önmagában ezeken a felületeken túl gyakran növeli az ilyen felületek érzékenységét - hasonlóan a drótvázas vonalak képéhez. Egy háromdimenziós felület és kontúrvonalak egyidejű megépítéséhez a kontúrvonal3d függvényt szolgálja. Az alkalmazásának egyik példája az 1. ábrán látható. 13.35.

Ábra. 13.34. Vektortér építése háromdimenziós térben.
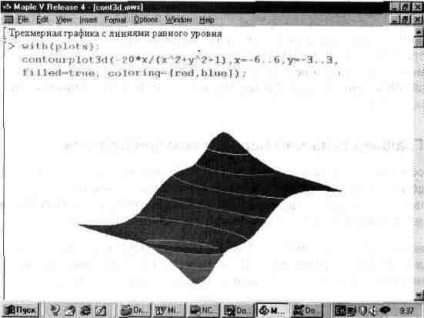
Ábra. 13.35. Kontúrvonalakkal rendelkező háromdimenziós felület grafikonja.
A láthatóság javítása érdekében ez a grafikon finomítható a diagram formázás eszköztárával. Különösen a funkcionális színezés szerepel, és az ábra látószögei kerülnek kiválasztásra, ahol az ábrán látható mélység és csúcs láthatóan látható.
13.6.9. A komplex térbeli alakzatok vizualizációjának technikája
A fenti meglehetősen egyszerű példák ötleteket adnak a geometriai alakzatok nagyfokú megjelenítéséről a telek csomag segítségével. Itt megnézzük még néhány példát a háromdimenziós ábrák megjelenítésére. Sokan láttak olyan induktorokat, amelyekben az egyik vagy másik átmérőjű huzal egy toroid mágneses magra van feltekerve. Az ilyen tekercs matematikai absztrakcióját az 1. ábrán mutatjuk be. 13.36.
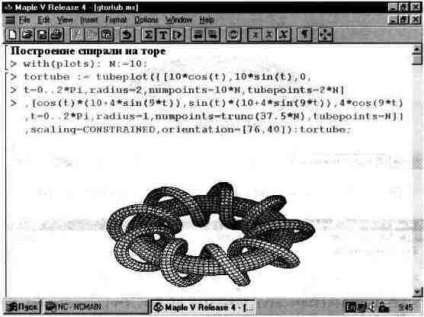
Ábra. 13.36. A teteje kanyargós - vastag spirál.
A dokumentumban (13.36. Ábra) az aktiválási csövek meglehetősen nagy számú opcióparamétert használnak. Nem mindig hatása nyilvánvaló. Ezért a 3. ábrán. A 13.37. Ábra három egymást keresztező tori konstrukcióját mutatja, amelyek különböző szerkezetűek. Ez a szám szintén ábrázolja a grafikus objektumok (a p1, p2 és p3 függvények által képviselt) lehetőségeinek ábrázolását a függvény tubeplot segítségével.
Számos esetben grafikusan ábrázolt számadatok alakíthatók ki azonos típusú adatok kombinációjával. Ilyen példa egy ilyen grafikonra