Fizikai osztály
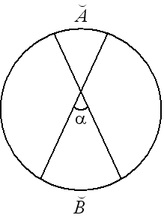
Tétel (szögek a metsző akkordok között). A két egymást keresztező akkord közötti szög megegyezik az általuk vágott ívek félösszegével:.
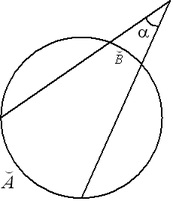
Tétel (szögek közötti szög). Az egyik pontból húzódó két zárószög közötti szög megegyezik a nagyobb és a kisebb ívek fél közötti különbségével.
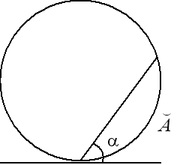
Tétel (az érintő és az akord közötti szög az érintési ponton keresztül). Az érintő és az akkord közötti érintkezési pont az érintőpontra húzva egyenlő az ív lekerekített fele.
A tétel (az érintő és a szekvencia közötti szög). Az érintő és a szekvencia közötti szög megegyezik az általuk vágott ívek fél-különbségével:.
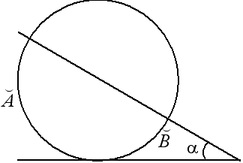
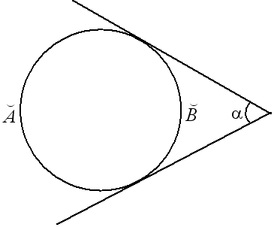
Tétel (tangensek közötti szög). Az egyik pontból húzott két érintő közötti szög megegyezik a nagyobb és a kisebb ívek fél közötti különbségével: