Finomít a spline a mathcadban
A MathCAD beágyazása
Ellentétben egy interpoláló spline-vel. áthaladó ismert pont i, fi> és már megvalósított MathCAD segítségével beépített funkciók és interpolált CSPLINE. A kiegyenlítő spline nem szükséges a méréseken átmenni. De ez sokkal rugalmasabb, és képes, ha konfigurálva, hogy kompenzálja a „rendellenes” dimenziók vagy egyszerűen „pótolni” az adatokat jobb, mint a OLS (vagy pontosabban, jobb - egy „kitörés” fi nem „pull” felfelé vagy lefelé az egész simító spline, ellentétben a polinom MLS teljesítmény alapú).
A probléma megfogalmazása a következő: tegyük fel, hogy az x1 rácson ahol h = x-xi a legközelebbi rács csomóponttól való távolság, c3, i. c2, i. c1, i. i = 1, 2. N-1 a kiegyenlítő spline együtthatója az i-es intervallumon az x tengely mentén. és yi az xi rács csomópontokon számított kiegyenlítő spline értékei. i = 1, 2. N. Általánosságban elmondható, hogy ezeknek a paramétereknek a kiválasztása külön feladat. A javasolt megoldásnál egy simítási spline kialakítása két funkcióval történik. SmoothSpline funkció (x, f, DF, SM) visszaadja egy objektum, amely egy sor együtthatók c a simító spline dimenziója 3 * (N-1) és y vektor értékeit a simítási spline rácsponti (dimenzió N). A funkciókódot itt nem adják meg a bulkiness - egy és fél oldal. A csatolt fájl letöltésével láthatja, de a következő funkciót hívhatja:

hívja a SmoothSpline funkciót
Vegye figyelembe, hogy a harmadik dimenzió „rendkívül” és a többi értékek a F (xi) = xi 2. Ennek megfelelően a felfújt df3 súlya (a továbbiakban, az elemek a mátrixok és vektorok vannak számozva az egyik, így MathCAD fájl kezdődik meghatározásával egy olyan rendszer változó ORIGIN: = 1).
Az is látható, hogy jó (az N kis értékei esetén) a sm smootion paraméter értékének kiválasztása.
A függvény a forrásadatok hibáira reagál - ilyen például a kettőnél rövidebb rácscsomópontok száma és a szigorú rendelés hiánya a xi értékek növelésével.
A függvény továbbá csak a 7 * (N + 2) méretű szolgáltatás valós tömbjét használja. azaz eléggé gazdaságos a memóriából.
A tesztet és annak eredményét az MSU Research Computing Center anyagaival ellenőrizték, minden egybeesett :)
A második funkció - GetSmoothSpline (x, dx, y, c) részt vesz az építőiparban az ismert simító spline együttható mátrix és a C értékeket a spline yi xi rács csomópontok. x a függvényen belül változik X1 xlength (x) dx egy lépést. A függvény egy mátrix két oszlop vektorok - tartalmazza az első érték az érvelés a második - a számított értékek a spline. Használja a funkciót, majd grafikusan megjeleníti a simítás eredményeit, például:
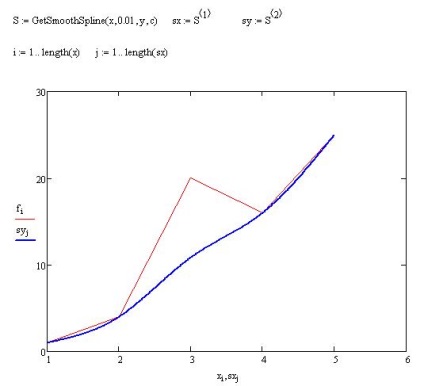
hívja a GetSmoothSpline funkciót
A második példa mutatja, hogy a simító spline képes megbirkózni a „abnormális” mérések adódó tevékenysége a nép ellenségei az olyan hibák, és nem fér bele a „big picture”.
Az adatok ebben az időben programozottan fognak generálni, egyszerűen eltávolítva őket egy szinuszos részből, majd néhány dimenzió nagyon eltér a többiektől:

adatok "anomális" mérésekkel
Így sikerült a két homoszexuális "kibocsátás" simító spline:
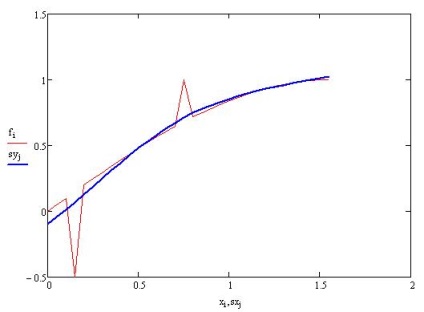
adatfeldolgozás rendellenes mérésekkel, simító spline
Látható, hogy szinte észre sem vette az eltéréseket.
Nos, még jobbat akarsz - indokolni a csomópontok súlyát és a simító paramétert.
Természetesen a simítás spline nem mindenható - például, ha „peremelchit” rács és túlzásba a számát „anomáliák”, mehet a „házal”, akkor az ilyen adatokat feldolgozó kellene vonni a gép képes figyelembe venni a minőségi eleve korlátok ( „de ebben az intervallumban függvénynek növelnie kell! "). Ilyen eszköz ismert leíró görbék, de cikket róluk, nem írtam sokáig, talán soha :)