Mágikus tér és palindromok
Mágikus négyzetek és palindromok George Alexandrovtól
Kedves Evgeny!
Küldök neked egy módszert egy olyan furcsa sorrendű mágikus négyzet létrehozására, amelyet magam is kifejlesztettem. A Bachet, Luber és mások módjai széles körben ismertek. De a megoldás talán a legegyszerűbb. Ezt a mellékelt illusztrációk jól láthatják. Először egy gyémánt alakú (sárga) magot választanak ki, amelyet rendszeresen töltöttek be páratlan számú számmal. Ezután a lekerekített magot tükrözéssel választjuk meg, a lépcsős háromszöget a keret két oldalához viszonyítva. Ez a rendszermag rendszeresen tölti meg a páros számú számot is. Ezután a vízszintes, függőleges és átlós háromszög alakú elemek egyszerű átvitelét végezzük. Még akkor is megkaptam a szellemet, amikor megkaptam!
Még a kétség is felmerült: talán nem vagyok úttörő? De bármennyire is próbáltam megtalálni valami hasonlóat az irodalomban, nem találtam semmit.
Ha a "Görögdinnye" olvasója képes lesz megtalálni a forrást, akkor kérlek, tájékoztassam a renuar911 [dog] yandex.ru-ról
Tisztelettel, Georgi Aleksandrov.
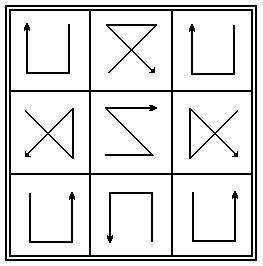
A páratlan sorrendű mágikus négyzet létrehozásának módja.
Ezt a módszert Georgy Alexandrov fejlesztette ki
A mágikus négyzet a kettős paritás sorrendjében.
A mágikus összeg az összes egyszerűsített négyzetben 2,5 n. vagyis a mi esetünkben 15
A nagyobb tisztaság kedvéért az utóbbi megoldás grafikailag leginkább ábrázolható:
Annak érdekében, hogy a következő egyszerűsített mágikus négyzetet, azaz az n = 10 sorrendet felépítsük, elegendő a feltételes ikonok övének hozzáadása a peremhez:
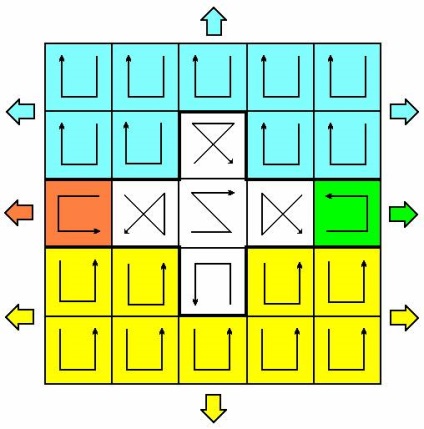
Az elszigetelt vízszintes folyosó, valamint két kiterjedt festett terület határtalanul kiterjed az oldalára, lehetővé téve ezáltal a 4k + 2-es sorrend nagyobb méretű matricákat. Minden színes nyíl azt jelzi, hogy ebben az irányban nem kell más ikonokat bevinni.
Így csökkentettük a problémát egy piszkos sorrendű mágikus négyzet létrehozásával. Ebben a 2 x 2-es cellában az azonosított számok sorozata van.
Ugyanúgy, mint egy puszta sorrendű mágikus négyzet esetében, két magot különböztetünk meg: egyenletes és furcsa, a feltételes ikonok megőrzése, amikor cellákat továbbítanak. Ezután egy egyszerű, természetes számsorozatot írunk le, egymás után egy páratlan rendszermagról páros számra és vissza. A következő ábra a töltőállomások kezdeti szakaszát mutatja.
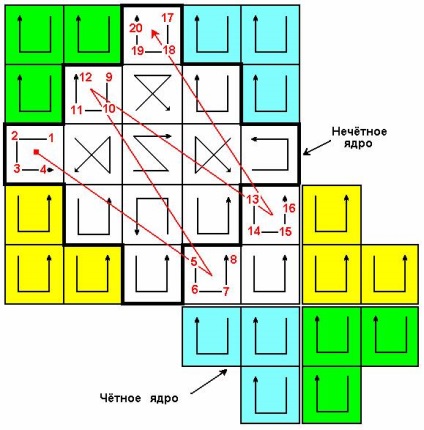
Ha az összes szám helyes, akkor a következőket kapjuk: