A logikai függvények minimalizálása a Quine módszerrel
Logikai függvények minimalizálása a Quine módszerrel
Quine módszere egy DNP vagy CNF függvénynek egy minimális számú és minimális változó-készletet képvisel. [1] [2] [3]
A funkció átalakítása két szakaszra bontható:
- az első szakaszban a kanonikus formáról (SDNF vagy SKNF) való átmenet az úgynevezett rövidített formára;
- a második szakaszban - a csökkentett formáról a minimálisra való átmenet.
Az első szakasz (csökkentett forma beszerzése)
Képzeljük el, hogy az adott funkció az SDNF-ben van jelen. Az első szakaszban az átalakulás két lépést tesz:
A ragasztási művelet a formanyomtatványhoz tartozó párok megállapítására, illetve a következő kifejezésekre való átalakításra korlátozódik :. A w ragasztási eredmények most kiegészítő szerepet töltenek be.
Ezután egy abszorpciós műveletet hajtanak végre. Az egyenlőségen alapul (a kifejezés elnyeli a kifejezést). E cselekvés következtében minden más változó által elnyelt kifejezést törölnek a logikai kifejezésből, amelynek eredményeit a ragasztási műveletben kapják meg.
Az első szakasz mindkét művelete elvégezhető mindaddig, amíg ez megtörténhet.
E műveletek alkalmazását a táblázat tartalmazza:
A ragasztási művelet eredménye szükséges ahhoz, hogy a funkciót a második szakaszba (abszorpció)
A ragasztás eredményének tagjai
A tag elnyeli az eredeti kifejezés tartalmát, azaz az első és negyedik tagot. Ezek a tagok törölve. A kifejezés elnyeli a második és a harmadik, és a kifejezés az eredeti kifejezés ötödik szakasza.
Mindkét művelet megismétlése a következő kifejezést eredményezi:
Ott ragasztott pár tagok és (ragasztás tagok és egy pár vezet ugyanarra az eredményre), ragasztás következtében elnyeli 2-, 3-, 4-, 5-én szempontjából az expressziót. A ragasztás és az abszorpció műveleteinek további végrehajtása lehetetlen, a kifejezés csökkentett formája egy adott funkcióra (ebben az esetben egybeesik a minimális formával)
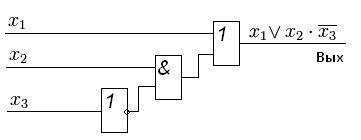
Funkcióblokk diagram
A rövidített formanyomtatványokat (a mi esetünkben ez) a funkció egyszerű implikációinak nevezzük. Végül a legegyszerűbb kifejezést kaptuk, ha összehasonlítjuk a kezdeti verzióval (CDNF). Az ilyen elemek szerkezeti rajza az ábrán jobbra látható.
A második szakasz (a minimális forma megszerzése)
Mint az első szakaszban, az eredményes egyenlőség olyan tagokat is tartalmazhat, akiknek megszüntetése semmilyen módon nem befolyásolja a végeredményt. A minimalizálás következő fázisa az ilyen változók eltávolítása. Az alábbi táblázat tartalmazza a függvény igazságértékét, a következő CDNF gyűjtődik.
PDNF. A táblából összegyűjtött adatok a következők:
A végső kifejezést a ragasztási és abszorpciós műveletek újrafelhasználásával érik el:
Ennek a kifejezésnek a tagjai egyszerű kifejezésminták. A csökkentett formától a minimálisig terjedő átmenetet egy implikáló mátrix segítségével végezzük.
Az adott funkció CDNF tagjai illeszkednek az oszlopokba és a sorokba - egyszerű implikátorok, vagyis a rövidített formák tagjai. A CDNF tagjai oszlopai megjelennek. Egyéni egyszerű implikátorok felszívódnak. Az alábbi táblázatban egy egyszerű implikáns elnyeli a tagokat és (az első és a második oszlopban a kereszteket helyezzük el).
Az implicit mátrix
A második implikáns elnyeli a CDNF első és harmadik tagját (keresztek jelzik) stb. A kizárás nélküli nemkívánatos anyagok egy magot képeznek. Az ilyen implikánsokat a fenti mátrixból határozzuk meg. Mindegyiküknek legalább egy oszlopa van, amelyet csak ez a befoglaló átfedi.
Példánkban a mag magában foglalja a következõket és (átfedi a második és a hatodik oszlopot). Kizárás a rövidített formában egyidejűleg valamennyi implicants amely kívül esik a mag, ez lehetetlen, hiszen a kizárás egyik implicants viszont egy másik felesleges az a tagja.
Minimális forma elég lehet választani implicants, non-core, mint egy minimális számú minimális számú betű minden ilyen implicants, amely biztosítani fogja az átfedés az összes oszlopot, nem átlapolt törzstagok. Ebben a példában implicants szükséges a zónán kívül blokk harmadik és negyedik oszlopa a mátrix. Ez úgy érhető el különböző módokon, hanem azért, mert szükséges, hogy kiválassza a minimális számú implicants, akkor nyilvánvaló, hogy az átfedés az oszlopok kell kiválasztani imlikantu.
Az adott funkció minimális diszjunktív normál formája (MDNF):
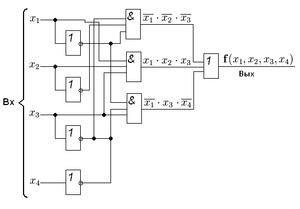
Kattintson a képre a nagyításhoz.
Az e kifejezésnek megfelelő szerkezeti sémát a bal oldali ábra mutatja. A rövidített rendszerről az MDNF-re való áttérést a felesleges tagok - az implicit és a. Mutassuk meg a tagok ilyen kivételének elfogadhatóságát logikai kifejezéssel.
Implikánsok és azonosak a naplóval. 1, az alábbi argumentumértékek esetén: = 0, = 0, = 0 és = 1, = 1, = 0.
A szerepe ezeknek implicants szempontjából kondenzált alakja a funkció csak a készletek a csökkent érv függvényértékeket hozzárendelni értéke 1. Azonban ezeket a csomagokat a függvény egyenlő 1 a többiek implicants kifejezést. Valóban, helyettesítjük egy sor értéket a fenti (a) képletben. kapunk:
- = 0, = 0, = 0
;
- = 1, = 1, = 0
;
A módszer alkalmazása a minimális CNF eléréséhez
A Minimum Conjunctive Normal Form (ICPF) eléréséhez a Quine módszerrel a következő kritériumokat kell bevezetni:
- a minimálisra csökkentése nem az SDNF. de az SKNF funkciói;
- A ragasztott párok tagjai: vagy;
- Az abszorpciós művelet szabálya a következő: